
Reeb stability theorem
Encyclopedia
In mathematics
, Reeb stability theorem, named after Georges Reeb
, asserts that if one leaf of a codimension
-one foliation
is closed
and has finite fundamental group
, then all the leaves are closed and have finite fundamental group.
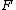 be a
be a 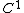 , codimension
, codimension 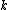 foliation
foliation
of a manifold
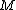 and
and 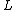 a compact
a compact
leaf with finite holonomy group
. There exists a neighborhood
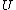 of
of  , saturated in
, saturated in  (also called invariant), in which all the leaves are compact with finite holonomy groups. Further, we can define a retraction
(also called invariant), in which all the leaves are compact with finite holonomy groups. Further, we can define a retraction  such that, for every leaf
such that, for every leaf 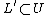 ,
,  is a covering
is a covering
with a finite number of sheets and, for each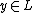 ,
,  is homeomorphic
is homeomorphic
to a disk
of dimension
k and is transverse to . The neighborhood
. The neighborhood  can be taken to be arbitrarily small.
can be taken to be arbitrarily small.
The last statement means in particular that, in a neighborhood of the point corresponding to a compact leaf
with finite holonomy, the space of leaves is Hausdorff
.
Under certain conditions the Reeb Local Stability Theorem may replace the Poincaré–Bendixson theorem
in higher dimensions. This is the case of codimension one, singular foliations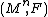 , with
, with 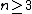 , and some center-type singularity in
, and some center-type singularity in 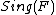 .
.
The Reeb Local Stability Theorem also has a version for a noncompact leaf.
. For certain classes of foliations, this influence is considerable.
Theorem: Let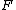 be a
be a 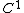 , codimension one foliation of a closed manifold
, codimension one foliation of a closed manifold 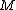 . If
. If  contains a compact
contains a compact
leaf with finite fundamental group
with finite fundamental group
, then all the leaves of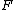 are compact, with finite fundamental group. If
are compact, with finite fundamental group. If 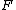 is transversely orientable
is transversely orientable
, then every leaf of is diffeomorphic
is diffeomorphic
to ;
;  is the total space
is the total space
of a fibration
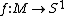 over
over 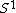 , with fibre
, with fibre 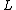 , and
, and 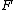 is the fibre foliation,
is the fibre foliation, 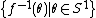 .
.
This theorem holds true even when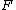 is a foliation of a manifold with boundary, which is, a priori, tangent
is a foliation of a manifold with boundary, which is, a priori, tangent
on certain components of the boundary
and transverse on other components. In this case it implies Reeb sphere theorem
.
Reeb Global Stability Theorem is false for foliations of codimension greater than one. However, for some special kinds of foliations one has the following global stability results:
Theorem: Let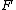 be a complete conformal
be a complete conformal
foliation of codimension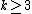 of a connected
of a connected
manifold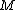 . If
. If 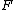 has a compact leaf with finite holonomy group
has a compact leaf with finite holonomy group
, then all the leaves of are compact with finite holonomy group.
are compact with finite holonomy group.
Theorem: Let be a holomorphic foliation of codimension
be a holomorphic foliation of codimension 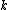 in a compact complex Kähler manifold
in a compact complex Kähler manifold
. If has a compact
has a compact
leaf with finite holonomy group
then every leaf of is compact with finite holonomy group.
is compact with finite holonomy group.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Reeb stability theorem, named after Georges Reeb
Georges Reeb
Georges Henri Reeb was a French mathematician. He worked in differential topology, differential geometry, differential equations, topological dynamical systems theory and non-standard analysis....
, asserts that if one leaf of a codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
-one foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
is closed
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
and has finite fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, then all the leaves are closed and have finite fundamental group.
Reeb local stability theorem
Theorem: Let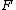 be a
be a 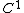 , codimension
, codimension 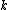 foliation
foliationFoliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
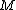 and
and 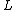 a compact
a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
leaf with finite holonomy group
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
. There exists a neighborhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
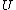 of
of  , saturated in
, saturated in  (also called invariant), in which all the leaves are compact with finite holonomy groups. Further, we can define a retraction
(also called invariant), in which all the leaves are compact with finite holonomy groups. Further, we can define a retraction  such that, for every leaf
such that, for every leaf 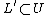 ,
,  is a covering
is a coveringCovering
-Mathematics:*In topology:** Covering map, a function from one space to another with uniform local neighborhoods** Cover , a system of sets whose union is a given topological space...
with a finite number of sheets and, for each
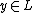 ,
,  is homeomorphic
is homeomorphicHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to a disk
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
of dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
k and is transverse to
 . The neighborhood
. The neighborhood  can be taken to be arbitrarily small.
can be taken to be arbitrarily small.The last statement means in particular that, in a neighborhood of the point corresponding to a compact leaf
with finite holonomy, the space of leaves is Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
.
Under certain conditions the Reeb Local Stability Theorem may replace the Poincaré–Bendixson theorem
Poincaré–Bendixson theorem
In mathematics, the Poincaré–Bendixson theorem is a statement about the long-term behaviour of orbits of continuous dynamical systems on the plane.-Theorem:...
in higher dimensions. This is the case of codimension one, singular foliations
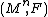 , with
, with 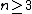 , and some center-type singularity in
, and some center-type singularity in 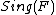 .
.The Reeb Local Stability Theorem also has a version for a noncompact leaf.
Reeb global stability theorem
An important problem in foliation theory is the study of the influence exerted by a compact leaf upon the global structure of a foliationFoliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
. For certain classes of foliations, this influence is considerable.
Theorem: Let
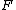 be a
be a 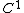 , codimension one foliation of a closed manifold
, codimension one foliation of a closed manifold 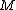 . If
. If  contains a compact
contains a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
leaf
 with finite fundamental group
with finite fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, then all the leaves of
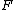 are compact, with finite fundamental group. If
are compact, with finite fundamental group. If 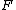 is transversely orientable
is transversely orientableOrientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
, then every leaf of
 is diffeomorphic
is diffeomorphicDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to
 ;
;  is the total space
is the total spaceFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
of a fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
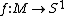 over
over 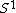 , with fibre
, with fibre 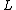 , and
, and 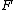 is the fibre foliation,
is the fibre foliation, 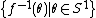 .
.This theorem holds true even when
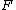 is a foliation of a manifold with boundary, which is, a priori, tangent
is a foliation of a manifold with boundary, which is, a priori, tangentTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
on certain components of the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
and transverse on other components. In this case it implies Reeb sphere theorem
Reeb sphere theorem
In mathematics, Reeb sphere theorem, named after Georges Reeb, states that-Morse foliation:A singularity of a foliation F is of Morse type if in its small neighborhood all leaves of the foliation are levels of a Morse function, being the singularity a critical point of the function...
.
Reeb Global Stability Theorem is false for foliations of codimension greater than one. However, for some special kinds of foliations one has the following global stability results:
- In the presence of a certain transverse geometric structure:
Theorem: Let
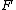 be a complete conformal
be a complete conformalConformal geometry
In mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
foliation of codimension
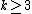 of a connected
of a connectedConnectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
manifold
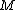 . If
. If 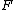 has a compact leaf with finite holonomy group
has a compact leaf with finite holonomy groupHolonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
, then all the leaves of
 are compact with finite holonomy group.
are compact with finite holonomy group.- For holomorphicComplex manifoldIn differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
foliations in complex Kähler manifoldKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
:
Theorem: Let
 be a holomorphic foliation of codimension
be a holomorphic foliation of codimension 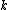 in a compact complex Kähler manifold
in a compact complex Kähler manifoldKähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
. If
 has a compact
has a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
leaf with finite holonomy group
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
then every leaf of
 is compact with finite holonomy group.
is compact with finite holonomy group.

