
Lagrangian Grassmannian
Encyclopedia
In mathematics
, the Lagrangian Grassmannian is the smooth manifold of Lagrangian subspaces of a real symplectic vector space
V. Its dimension is n(n+1)/2 (where the dimension of V is 2n). It may be identified with the homogeneous space
where U(n) is the unitary group
and O(n) the orthogonal group
. After Vladimir Arnold
it is denoted by Λ(n).
A complex Lagrangian Grassmannian is the complex homogeneous manifold
of Lagrangian subspaces of a complex symplectic vector space
V of dimension 2n. It may be identified with the homogeneous space
of complex dimension n(n+1)/2
where Sp(n) is the complex symplectic group
.
: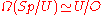 , and
, and  – they are thus exactly the homotopy groups of the stable orthogonal group, up to a shift in indexing (dimension).
– they are thus exactly the homotopy groups of the stable orthogonal group, up to a shift in indexing (dimension).
In particular, the fundamental group
of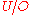 is infinite cyclic, with a distinguished generator given by the square of the determinant
is infinite cyclic, with a distinguished generator given by the square of the determinant
of a unitary matrix, as a mapping to the unit circle
. Its first homology group is therefore also infinite cyclic, as is its first cohomology group. Arnold showed that this leads to a description of the Maslov index, introduced by V. P. Maslov.
For a Lagrangian submanifold M of V, in fact, there is a mapping
which classifies its tangent space
at each point (cf. Gauss map
). The Maslov index is the pullback via this mapping, in
of the distinguished generator of
s of a symplectic vector space may be assigned a Maslov index; it will be an integer if the path is a loop, and a half-integer in general.
If this path arises from trivializing the symplectic vector bundle over a periodic orbit of a Hamiltonian vector field
on a symplectic manifold
or the Reeb vector field
on a contact manifold, it is known as the Conley-Zehnder index. It computes the spectral flow of the Cauchy-Riemann
-type operators that arise in Floer homology
.
It appeared originally in the study of the WKB approximation
and appears frequently in the study of quantization
and in symplectic geometry and topology. It can be described as above in terms of a Maslov index for linear Lagrangian submanifolds.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lagrangian Grassmannian is the smooth manifold of Lagrangian subspaces of a real symplectic vector space
Symplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
V. Its dimension is n(n+1)/2 (where the dimension of V is 2n). It may be identified with the homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
- U(n)/O(n)
where U(n) is the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
and O(n) the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
. After Vladimir Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
it is denoted by Λ(n).
A complex Lagrangian Grassmannian is the complex homogeneous manifold
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
of Lagrangian subspaces of a complex symplectic vector space
Symplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
V of dimension 2n. It may be identified with the homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
of complex dimension n(n+1)/2
- Sp(n)/U(n)
where Sp(n) is the complex symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
.
Topology
The stable topology of the Lagrangian Grassmannian and complex Lagrangian Grassmannian is completely understood, as these spaces appear in the Bott periodicity theoremBott periodicity theorem
In mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by , which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy...
:
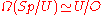 , and
, and  – they are thus exactly the homotopy groups of the stable orthogonal group, up to a shift in indexing (dimension).
– they are thus exactly the homotopy groups of the stable orthogonal group, up to a shift in indexing (dimension).In particular, the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of
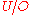 is infinite cyclic, with a distinguished generator given by the square of the determinant
is infinite cyclic, with a distinguished generator given by the square of the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a unitary matrix, as a mapping to the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
. Its first homology group is therefore also infinite cyclic, as is its first cohomology group. Arnold showed that this leads to a description of the Maslov index, introduced by V. P. Maslov.
For a Lagrangian submanifold M of V, in fact, there is a mapping
- M → Λ(n)
which classifies its tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at each point (cf. Gauss map
Gauss map
In differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...
). The Maslov index is the pullback via this mapping, in
- H1(M, Z)
of the distinguished generator of
- H1(Λ(n), Z).
Maslov index
A path of symplectomorphismSymplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
s of a symplectic vector space may be assigned a Maslov index; it will be an integer if the path is a loop, and a half-integer in general.
If this path arises from trivializing the symplectic vector bundle over a periodic orbit of a Hamiltonian vector field
Hamiltonian vector field
In mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
on a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
or the Reeb vector field
Reeb vector field
In mathematics, the Reeb vector field, named after the French mathematician Georges Reeb, is a notion that appears in various domains of contact geometry including:...
on a contact manifold, it is known as the Conley-Zehnder index. It computes the spectral flow of the Cauchy-Riemann
Cauchy-Riemann equations
In mathematics, the Cauchy–Riemann differential equations in complex analysis, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which must be satisfied if we know that a complex function is complex differentiable...
-type operators that arise in Floer homology
Floer homology
Floer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology. First introduced by Andreas Floer in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory arising as an infinite dimensional analog of finite...
.
It appeared originally in the study of the WKB approximation
WKB approximation
In mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients...
and appears frequently in the study of quantization
Quantization
Quantization is the procedure of constraining something from a relatively large or continuous set of values to a relatively small discrete set...
and in symplectic geometry and topology. It can be described as above in terms of a Maslov index for linear Lagrangian submanifolds.

