Floer homology
Encyclopedia
Floer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology
. First introduced by Andreas Floer
in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory
arising as an infinite dimensional analog of finite dimensional Morse homology
. A similar construction, also introduced by Floer, provides a homology theory associated to three-dimensional manifolds. This theory, along with a number of its generalizations, plays a fundamental role in current investigations into the topology of three- and four-dimensional manifolds. Using techniques from gauge theory
, these investigations have provided surprising new insights into the structure of three- and four-dimensional differentiable manifold
s.
Floer homology is typically defined by associating an infinite dimensional manifold to the object of interest. In the symplectic version, this is the free loop space of a symplectic manifold, while in the three-dimensional manifold version, it is the space of SU(2)-connections
on a three-dimensional manifold. Loosely speaking, Floer homology is the Morse homology computed from a natural function on this infinite dimensional manifold. This function is the symplectic action on the free loop space or the Chern–Simons function on the space of connections. A homology theory is formed from the vector space spanned by the critical points
of this function. A linear endomorphism
of this vector space is defined by counting the function's gradient
flow lines connecting two critical points. Floer homology is then the quotient vector space
formed by identifying the image of this endomorphism inside its kernel
.
and a nondegenerate symplectomorphism
of it. If the symplectomorphism is Hamiltonian, the homology arises from studying the symplectic action functional on the (universal cover of the) free loop space of a symplectic manifold. SFH is invariant under Hamiltonian isotopy of the symplectomorphism.
Here, nondegeneracy means that 1 is not an eigenvalue of the derivative of the symplectomorphism at any of its fixed points. This condition implies that the fixed points will be isolated. SFH is the homology of the chain complex generated by the fixed points
of such a symplectomorphism, where the differential counts certain pseudoholomorphic curve
s in the product of the real line and the mapping torus
of the symplectomorphism. This itself is a symplectic manifold of dimension two greater than the original manifold. For an appropriate choice of almost complex structure, punctured holomorphic curves in it have cylindrical ends asymptotic to the loops in the mapping torus corresponding to fixed points of the symplectomorphism. A relative index may be defined between pairs of fixed points, and the differential counts the number of holomorphic cylinders with relative index 1.
The symplectic Floer homology of a Hamiltonian symplectomorphism is isomorphic to the singular homology of the underlying manifold. Thus, the sum of the Betti numbers of that manifold yields the lower bound predicted by one version of the Arnold conjecture for the number of fixed points for a nondegenerate symplectomorphism. The SFH of a Hamiltonian symplectomorphism also has a pair of pants
product which is a deformed cup product
equivalent to quantum cohomology
. A version of the product also exists for non-exact symplectomorphisms.
For the cotangent bundle of a manifold M, the Floer homology depends on the choice of Hamiltonian due to its noncompactness. For Hamiltonians that are quadratic at infinity, the Floer homology is the singular homology of the free loop space of M (proofs of various versions of this statement are due to Viterbo, Salamon–Weber, Abbondandolo–Schwarz, and Cohen).
The symplectic version of Floer homology figures in a crucial way in the formulation of the homological mirror symmetry conjecture.
three-manifolds. Each yields three types of homology groups, which fit into an exact triangle. Heegaard Floer and Seiberg–Witten Floer homology also yield knot invariants which are formally similar to the combinatorially-defined Khovanov homology
.
These are closely related to the Donaldson and Seiberg invariants of 4-manifolds, as well as Taubes's Gromov invariant of symplectic 4-manifolds; the differentials of the corresponding three-manifold homologies to these theories are studied by considering solutions to the relevant differential equations (Yang–Mills
, Seiberg–Witten, and Cauchy–Riemann, respectively) on the 3-manifold cross R. The 3-manifold Floer homologies should also be the targets of relative invariants for four-manifolds with boundary, related by gluing constructions to the invariants of a closed 4-manifold obtained by gluing together bounded 3-manifolds along their boundaries. (This is closely related to the notion of a topological quantum field theory
.) For Heegaard Floer homology, the 3-manifold homology was defined first, and an invariant for closed 4-manifolds was later defined in terms of it.
There are also extensions of the 3-manifold homologies to 3-manifolds with boundary: sutured Floer homology (Juhász) and bordered Floer homology (Lipshitz–Ozsváth–Thurston). These are expected to be related to the invariants for closed 3-manifolds by gluing formulas for the Floer homology of a 3-manifold described as the union along the boundary of two 3-manifolds with boundary.
The three-manifold Floer homologies also come equipped with a distinguished element of the homology if the three-manifold is equipped with a contact structure beginning with Kronheimer and Mrowka in the Seiberg–Witten case. (A choice of contact structure is required to define embedded contact homology but not the others.)
These theories all come equipped with a priori relative gradings; these have been lifted to absolute gradings (by assigning homotopy classes of 2-plane fields) for SWF, and using the SWF-ECH isomorphism, ECH.
introduced by Floer himself. It is obtained using the Chern–Simons functional on the space of connections
on a principal
SU(2)-bundle over the three-manifold. Its critical points are flat connections and its flow lines are instanton
s, i.e. anti-self-dual connections on the three-manifold crossed with the real line.
Soon after Floer's introduction of Floer homology, Donaldson realized that cobordisms induce maps. This was the first instance
of the structure that came to be known as a Topological Quantum Field Theory.
s (equipped with a spinc structure) that is generated by solutions to Seiberg–Witten equations on a 3-manifold and whose differential counts invariant solutions to the Seiberg–Witten equations on the product of a 3-manifold and the real line.
SWF was constructed rigorously in the book of Peter Kronheimer and Tomasz Mrowka
. Before that, SWF for rational homology 3-spheres had been constructed by Kim Froyshov, and certain cases had also been constructed using finite-dimensional approximation in by Ciprian Manolescu
and Kronheimer.
Cliff Taubes has proved that SWF and ECH are isomorphic.
and Zoltán Szabó
of a closed 3-manifold equipped with a spinc structure. It is computed using a Heegaard diagram
of the space via a construction analogous to Lagrangian Floer homology. In 2010, Kutluhan–Lee–Taubes and Colin–Ghiggini–Honda announced proofs that Heegaard Floer homology is isomorphic to embedded contact homology .
A knot in a three-manifold induces a filtration on the Heegaard Floer homology groups, and the filtered homotopy type is a powerful knot invariant
, which categorifies
the Alexander polynomial
. It was defined by Ozsváth and Szabó and independently by Jacob Rasmussen. It is known to detect knot genus. The knot Floer homology of a knot (as well as the Heegaard Floer homology of the double cover of S^3 branched over a knot) are related by spectral sequences to (variants of) Khovanov homology
. (Ozsvath–Szabo 2005).
Using grid diagrams for the Heegaard splittings, Heegaard Floer homology with coefficients in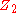
and the "HF hat" version of Heegaard Floer homology and the maps induced on it by cobordisms have been given combinatorial constructions by several authors starting out from initial work by Sucharit Sarkar. Similar constructions have yielded combinatorial constructions of knot Floer homology.
) to Seiberg–Witten Floer homology and (by work announced by Kutluhan–Lee–Taubes and by Colin-Ghiggini–Honda) to Heegaard Floer homology. It may be seen as an extension of Taubes's Gromov invariant
, known to be equivalent to the Seiberg–Witten invariant
, from closed symplectic 4-manifold
s to certain non-compact symplectic 4-manifolds (namely, a contact three-manifold cross R). Its construction is analogous to symplectic field theory, in that it is generated by certain collections of closed Reeb orbits and its differential counts certain holomorphic curves with ends at certain collections of Reeb orbits; it differs from SFT in technical conditions on the collections of Reeb orbits that generate it and in not counting all holomorphic curves with Fredholm index 1 with given ends, but only those which also satisfy a topological condition given by the "ECH index", which in particular implies that the curves considered are (mainly) embedded.
The Weinstein conjecture
that a contact 3-manifold has a closed Reeb orbit for any contact form holds on any manifold whose ECH is nontrivial, and was proved by Taubes using techniques closely related to ECH; extensions of this work yielded the isomorphism between ECH and SWF. Many constructions in ECH (including its well-definedness) rely upon this isomorphism.
The contact element of ECH has a particularly nice form: it is the cycle associated to the empty collection of Reeb orbits.
An analog of embedded contact homology may be defined for mapping tori of symplectomorphisms of a surface (possibly with boundary) and is known as periodic Floer homology, generalizing the symplectic Floer homology of surface symplectomorphisms. More generally, it may be defined with respect to any stable Hamiltonian structure on the 3-manifold.
Given three Lagrangian submanifolds L0, L1, and L2 of a symplectic manifold, there is a product structure on the Lagrangian Floer homology:
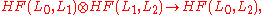
which is defined by counting holomorphic triangles (that is, holomorphic maps of a triangle whose vertices and edges map to the appropriate intersection points and Lagrangian submanifolds).
Papers on this subject are due to Fukaya, Oh, Ono, and Ohta; the recent work on "cluster homology" of Lalonde and Cornea offer a different approach to it. The Floer homology of a pair of Lagrangian submanifolds may not always exist; when it does, it provides an obstruction to isotoping one Lagrangian away from the other using a Hamiltonian isotopy.
along a surface
. Then the space of flat connections on 
modulo gauge equivalence is a symplectic manifold of dimension 6g − 6, where g is the genus
of the surface
. In the Heegaard splitting, 
bounds two different 3-manifolds; the space of flat connections modulo gauge equivalence on each 3-manifold with boundary (equivalently, the space of connections on 
that extend over each three manifold) is a Lagrangian submanifold of the space of connections on 
. We may thus consider their Lagrangian intersection Floer homology. Alternately, we can consider the Instanton Floer homology of the 3-manifold Y. The Atiyah-Floer conjecture asserts that these two invariants are isomorphic. Katrin Wehrheim
and Dietmar Salamon are working on a program to prove this conjecture.
conjecture of Maxim Kontsevich
predicts an equality between the Lagrangian Floer homology of Lagrangians in a Calabi–Yau manifold
and the Ext groups of coherent sheaves on the mirror Calabi–Yau manifold. In this situation, one should not focus on the Floer homology groups but on the Floer chain groups. Similar to the pair-of-pants product, one can construct multi-compositions using pseudo-holomorphic n-gons. These compositions satisfy the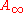 
-relations making the category of all (unobstructed) Lagrangian submanifolds in a symplectic manifold into an 
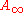-category, called the Fukaya category.
To be more precise, one must add additional data to the Lagrangian – a grading and a spin structure
. A Lagrangian with a choice of these structures is often called a brane in homage to the underlying physics. The Homological Mirror Symmetry conjecture states there is a type of derived Morita equivalence
between the Fukaya category of the Calabi–Yau
and a dg category underlying the bounded derived category
of coherent sheaves of the mirror, and vice-versa.
s between them, originally due to Yakov Eliashberg
, Alexander Givental
and Helmut Hofer. The symplectic field theory as well as its subcomplexes, rational symplectic field theory and contact homology, are defined as homologies of differential algebras, which are generated by closed orbits of the Reeb vector field
of a chosen contact form. The differential counts certain holomorphic curves in the cylinder over the contact manifold, where the trivial examples are the branched coverings of (trivial) cylinders over closed Reeb orbits. It further includes a linear homology theory, called cylindrical or linearized contact homology (sometimes, by abuse of notation, just contact homology), whose chain groups are vector spaces generated by closed orbits and whose differentials count only holomorphic cylinders. However, cylindrical contact homology is not always defined due to the presence of holomorphic discs. In situations where cylindrical contact homology makes sense, it may be seen as the (slightly modified) "Morse homology" of the action functional on the free loop space which sends a loop to the integral of the contact form alpha over the loop. Reeb orbits are the critical points of this functional.
SFT also associates a relative invariant of a Legendrian submanifold of a contact manifold known as relative contact homology
.
In SFT the contact manifolds can be replaced by mapping tori
of symplectic manifolds with symplectomorphisms. While the cylindrical contact homology is well-defined and given by the symplectic Floer homologies of powers of the symplectomorphism, (rational) symplectic field theory and contact homology can be considered as generalized symplectic Floer homologies. In the important case when the symplectomorphism is the time-one map of a time-dependent Hamiltonian, it was however shown that these higher invariants do not contain any further information.
whose ordinary homology is the desired Floer homology. Applying other homology theories to such a spectrum could yield other interesting invariants. This strategy was proposed by Ralph Cohen, John Jones, and Graeme Segal
, and carried out in certain cases for Seiberg–Witten–Floer homology by Kronheimer and Manolescu and for the symplectic Floer homology of cotangent bundles by Cohen.
moduli space
s of pseudoholomorphic curves. Hofer, in collaboration with Kris Wysocki and Eduard Zehnder, has developed new analytic foundations via their theory of polyfolds and a "general Fredholm theory". While the polyfold project is not yet fully completed, in some important cases transversality was shown using simpler methods.
of much of the theory. It is also connected it to existing invariants and structures and many insights into 3-manifold topology have resulted.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. First introduced by Andreas Floer
Andreas Floer
Andreas Floer was a German mathematician who made seminal contributions to the areas of geometry, topology, and mathematical physics, in particular the invention of Floer homology.-Life:...
in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
arising as an infinite dimensional analog of finite dimensional Morse homology
Morse homology
In mathematics, specifically in the field of differential topology, Morse homology is a homology theory defined for any smooth manifold. It is constructed using the smooth structure and an auxiliary metric on the manifold, but turns out to be topologically invariant, and is in fact isomorphic to...
. A similar construction, also introduced by Floer, provides a homology theory associated to three-dimensional manifolds. This theory, along with a number of its generalizations, plays a fundamental role in current investigations into the topology of three- and four-dimensional manifolds. Using techniques from gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, these investigations have provided surprising new insights into the structure of three- and four-dimensional differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s.
Floer homology is typically defined by associating an infinite dimensional manifold to the object of interest. In the symplectic version, this is the free loop space of a symplectic manifold, while in the three-dimensional manifold version, it is the space of SU(2)-connections
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
on a three-dimensional manifold. Loosely speaking, Floer homology is the Morse homology computed from a natural function on this infinite dimensional manifold. This function is the symplectic action on the free loop space or the Chern–Simons function on the space of connections. A homology theory is formed from the vector space spanned by the critical points
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
of this function. A linear endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
of this vector space is defined by counting the function's gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
flow lines connecting two critical points. Floer homology is then the quotient vector space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
formed by identifying the image of this endomorphism inside its kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
.
Symplectic Floer homology
Symplectic Floer Homology (SFH) is a homology theory associated to a symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
and a nondegenerate symplectomorphism
Symplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
of it. If the symplectomorphism is Hamiltonian, the homology arises from studying the symplectic action functional on the (universal cover of the) free loop space of a symplectic manifold. SFH is invariant under Hamiltonian isotopy of the symplectomorphism.
Here, nondegeneracy means that 1 is not an eigenvalue of the derivative of the symplectomorphism at any of its fixed points. This condition implies that the fixed points will be isolated. SFH is the homology of the chain complex generated by the fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of such a symplectomorphism, where the differential counts certain pseudoholomorphic curve
Pseudoholomorphic curve
In mathematics, specifically in topology and geometry, a pseudoholomorphic curve is a smooth map from a Riemann surface into an almost complex manifold that satisfies the Cauchy–Riemann equation. Introduced in 1985 by Mikhail Gromov, pseudoholomorphic curves have since revolutionized the study of...
s in the product of the real line and the mapping torus
Mapping torus
In mathematics, the mapping torus in topology of a homeomorphism f of some topological space X to itself is a particular geometric construction with f...
of the symplectomorphism. This itself is a symplectic manifold of dimension two greater than the original manifold. For an appropriate choice of almost complex structure, punctured holomorphic curves in it have cylindrical ends asymptotic to the loops in the mapping torus corresponding to fixed points of the symplectomorphism. A relative index may be defined between pairs of fixed points, and the differential counts the number of holomorphic cylinders with relative index 1.
The symplectic Floer homology of a Hamiltonian symplectomorphism is isomorphic to the singular homology of the underlying manifold. Thus, the sum of the Betti numbers of that manifold yields the lower bound predicted by one version of the Arnold conjecture for the number of fixed points for a nondegenerate symplectomorphism. The SFH of a Hamiltonian symplectomorphism also has a pair of pants
Pair of pants
In mathematics, a pair of pants is a simple two-dimensional surface resembling a pair of pants: topologically, it is a sphere with three holes in it...
product which is a deformed cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
equivalent to quantum cohomology
Quantum cohomology
In mathematics, specifically in symplectic topology and algebraic geometry, a quantum cohomology ring is an extension of the ordinary cohomology ring of a closed symplectic manifold. It comes in two versions, called small and big; in general, the latter is more complicated and contains more...
. A version of the product also exists for non-exact symplectomorphisms.
For the cotangent bundle of a manifold M, the Floer homology depends on the choice of Hamiltonian due to its noncompactness. For Hamiltonians that are quadratic at infinity, the Floer homology is the singular homology of the free loop space of M (proofs of various versions of this statement are due to Viterbo, Salamon–Weber, Abbondandolo–Schwarz, and Cohen).
The symplectic version of Floer homology figures in a crucial way in the formulation of the homological mirror symmetry conjecture.
Floer homology of three-manifolds
There are several conjecturally equivalent Floer homologies associated to closedClosed
Closed may refer to:Math* Closure * Closed manifold* Closed orbits* Closed set* Closed differential form* Closed map, a function that is closed.Other* Cloister, a closed walkway* Closed-circuit television...
three-manifolds. Each yields three types of homology groups, which fit into an exact triangle. Heegaard Floer and Seiberg–Witten Floer homology also yield knot invariants which are formally similar to the combinatorially-defined Khovanov homology
Khovanov homology
In mathematics, Khovanov homology is an invariant of oriented knots and links that arises as the homology of a chain complex. It may be regarded as a categorification of the Jones polynomial....
.
These are closely related to the Donaldson and Seiberg invariants of 4-manifolds, as well as Taubes's Gromov invariant of symplectic 4-manifolds; the differentials of the corresponding three-manifold homologies to these theories are studied by considering solutions to the relevant differential equations (Yang–Mills
Yang–Mills
Yang–Mills theory is a gauge theory based on the SU group. Wolfgang Pauli formulated in 1953 the first consistent generalization of the five-dimensional theory of Kaluza, Klein, Fock and others to a higher dimensional internal space...
, Seiberg–Witten, and Cauchy–Riemann, respectively) on the 3-manifold cross R. The 3-manifold Floer homologies should also be the targets of relative invariants for four-manifolds with boundary, related by gluing constructions to the invariants of a closed 4-manifold obtained by gluing together bounded 3-manifolds along their boundaries. (This is closely related to the notion of a topological quantum field theory
Topological quantum field theory
A topological quantum field theory is a quantum field theory which computes topological invariants....
.) For Heegaard Floer homology, the 3-manifold homology was defined first, and an invariant for closed 4-manifolds was later defined in terms of it.
There are also extensions of the 3-manifold homologies to 3-manifolds with boundary: sutured Floer homology (Juhász) and bordered Floer homology (Lipshitz–Ozsváth–Thurston). These are expected to be related to the invariants for closed 3-manifolds by gluing formulas for the Floer homology of a 3-manifold described as the union along the boundary of two 3-manifolds with boundary.
The three-manifold Floer homologies also come equipped with a distinguished element of the homology if the three-manifold is equipped with a contact structure beginning with Kronheimer and Mrowka in the Seiberg–Witten case. (A choice of contact structure is required to define embedded contact homology but not the others.)
These theories all come equipped with a priori relative gradings; these have been lifted to absolute gradings (by assigning homotopy classes of 2-plane fields) for SWF, and using the SWF-ECH isomorphism, ECH.
Instanton Floer homology
This is a three-manifold invariant connected to Donaldson theoryDonaldson theory
Donaldson theory is the study of smooth 4-manifolds using gauge theory. It was started by Simon Donaldson who proved Donaldson's theorem restricting the possible quadratic forms on the second cohomology group of a compact simply connected 4-manifold....
introduced by Floer himself. It is obtained using the Chern–Simons functional on the space of connections
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
on a principal
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
SU(2)-bundle over the three-manifold. Its critical points are flat connections and its flow lines are instanton
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
s, i.e. anti-self-dual connections on the three-manifold crossed with the real line.
Soon after Floer's introduction of Floer homology, Donaldson realized that cobordisms induce maps. This was the first instance
of the structure that came to be known as a Topological Quantum Field Theory.
Seiberg–Witten Floer homology
Seiberg–Witten Floer homology, also known as monopole Floer homology, is a homology theory of smooth 3-manifold3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s (equipped with a spinc structure) that is generated by solutions to Seiberg–Witten equations on a 3-manifold and whose differential counts invariant solutions to the Seiberg–Witten equations on the product of a 3-manifold and the real line.
SWF was constructed rigorously in the book of Peter Kronheimer and Tomasz Mrowka
Tomasz Mrowka
Tomasz Mrowka is a Polish American mathematician. He has been the Singer Professor of Mathematics at Massachusetts Institute of Technology since 2010. A graduate of MIT, he received the Ph.D. from University of California, Berkeley in 1988 under the direction of Clifford Taubes and Robion Kirby...
. Before that, SWF for rational homology 3-spheres had been constructed by Kim Froyshov, and certain cases had also been constructed using finite-dimensional approximation in by Ciprian Manolescu
Ciprian Manolescu
Ciprian Manolescu is a Romanian mathematician. He is presently an Associate Professor in the mathematics department at the University of California, Los Angeles....
and Kronheimer.
Cliff Taubes has proved that SWF and ECH are isomorphic.
Heegaard Floer homology
Heegaard Floer homology is an invariant due to Peter OzsváthPeter Ozsváth
Peter Steven Ozsváth is a professor of mathematics at Princeton University. He created, along with Zoltán Szabó, Heegaard Floer homology, a homology theory for 3-manifolds....
and Zoltán Szabó
Zoltán Szabó
Zoltán Szabó is a professor of mathematics at Princeton University. He created, along with Peter Ozsváth, Heegaard Floer homology, a homology theory for 3-manifolds. For this contribution to the field of topology, Ozsváth and Szabó were awarded the 2007 Oswald Veblen Prize in Geometry.He got his...
of a closed 3-manifold equipped with a spinc structure. It is computed using a Heegaard diagram
Heegaard splitting
In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.-Definitions:...
of the space via a construction analogous to Lagrangian Floer homology. In 2010, Kutluhan–Lee–Taubes and Colin–Ghiggini–Honda announced proofs that Heegaard Floer homology is isomorphic to embedded contact homology .
A knot in a three-manifold induces a filtration on the Heegaard Floer homology groups, and the filtered homotopy type is a powerful knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
, which categorifies
Categorification
In mathematics, categorification refers to the process of replacing set-theoretic theorems by category-theoretic analogues. Categorification, when done successfully, replaces sets by categories, functions with functors, and equations by natural isomorphisms of functors satisfying additional...
the Alexander polynomial
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
. It was defined by Ozsváth and Szabó and independently by Jacob Rasmussen. It is known to detect knot genus. The knot Floer homology of a knot (as well as the Heegaard Floer homology of the double cover of S^3 branched over a knot) are related by spectral sequences to (variants of) Khovanov homology
Khovanov homology
In mathematics, Khovanov homology is an invariant of oriented knots and links that arises as the homology of a chain complex. It may be regarded as a categorification of the Jones polynomial....
. (Ozsvath–Szabo 2005).
Using grid diagrams for the Heegaard splittings, Heegaard Floer homology with coefficients in
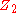and the "HF hat" version of Heegaard Floer homology and the maps induced on it by cobordisms have been given combinatorial constructions by several authors starting out from initial work by Sucharit Sarkar. Similar constructions have yielded combinatorial constructions of knot Floer homology.Embedded contact homology
Embedded contact homology, due to Michael Hutchings, is an invariant of 3-manifolds (with a distinguished second homology class, corresponding to the choice of a spinc structure in Seiberg–Witten Floer homology, isomorphic (by work of Clifford TaubesClifford Taubes
Clifford Henry Taubes is the William Petschek Professor of Mathematics at Harvard University and works in gauge field theory, differential geometry, and low-dimensional topology.-Early career:Taubes received his Ph.D...
) to Seiberg–Witten Floer homology and (by work announced by Kutluhan–Lee–Taubes and by Colin-Ghiggini–Honda) to Heegaard Floer homology. It may be seen as an extension of Taubes's Gromov invariant
Taubes's Gromov invariant
In mathematics, the Gromov invariant of Clifford Taubes counts embedded pseudoholomorphic curves in a symplectic 4-manifold...
, known to be equivalent to the Seiberg–Witten invariant
Seiberg–Witten invariant
In mathematics, Seiberg–Witten invariants are invariants of compact smooth 4-manifolds introduced by , using the Seiberg–Witten theory studied by during their investigations of Seiberg–Witten gauge theory....
, from closed symplectic 4-manifold
4-manifold
In mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
s to certain non-compact symplectic 4-manifolds (namely, a contact three-manifold cross R). Its construction is analogous to symplectic field theory, in that it is generated by certain collections of closed Reeb orbits and its differential counts certain holomorphic curves with ends at certain collections of Reeb orbits; it differs from SFT in technical conditions on the collections of Reeb orbits that generate it and in not counting all holomorphic curves with Fredholm index 1 with given ends, but only those which also satisfy a topological condition given by the "ECH index", which in particular implies that the curves considered are (mainly) embedded.
The Weinstein conjecture
Weinstein conjecture
In mathematics, the Weinstein conjecture refers to a general existence problem for periodic orbits of Hamiltonian or Reeb vector flows. More specifically, the current understanding is that a regular compact contact type level set of a Hamiltonian on a symplectic manifold should carry at least one...
that a contact 3-manifold has a closed Reeb orbit for any contact form holds on any manifold whose ECH is nontrivial, and was proved by Taubes using techniques closely related to ECH; extensions of this work yielded the isomorphism between ECH and SWF. Many constructions in ECH (including its well-definedness) rely upon this isomorphism.
The contact element of ECH has a particularly nice form: it is the cycle associated to the empty collection of Reeb orbits.
An analog of embedded contact homology may be defined for mapping tori of symplectomorphisms of a surface (possibly with boundary) and is known as periodic Floer homology, generalizing the symplectic Floer homology of surface symplectomorphisms. More generally, it may be defined with respect to any stable Hamiltonian structure on the 3-manifold.
Lagrangian intersection Floer homology
The Lagrangian Floer homology of two Lagrangian submanifolds of a symplectic manifold is the homology of a chain complex which is generated by the intersection points of the two submanifolds and whose differential counts pseudoholomorphic Whitney discs. The symplectic Floer homology of a symplectomorphism of M can be thought of as the special case of Lagrangian Floer homology in which the ambient manifold is M cross M and the Lagrangian submanifolds are the diagonal and the graph of the symplectomorphism. The construction of Heegaard Floer homology (see above) is based on a variant of Lagrangian Floer homology. The theory also appears in work of Seidel–Smith and Manolescu exhibiting what is conjectured to be part of the combinatorially-defined Khovanov homology as a Lagrangian intersection Floer homology.Given three Lagrangian submanifolds L0, L1, and L2 of a symplectic manifold, there is a product structure on the Lagrangian Floer homology:
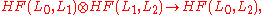
which is defined by counting holomorphic triangles (that is, holomorphic maps of a triangle whose vertices and edges map to the appropriate intersection points and Lagrangian submanifolds).
Papers on this subject are due to Fukaya, Oh, Ono, and Ohta; the recent work on "cluster homology" of Lalonde and Cornea offer a different approach to it. The Floer homology of a pair of Lagrangian submanifolds may not always exist; when it does, it provides an obstruction to isotoping one Lagrangian away from the other using a Hamiltonian isotopy.
Atiyah–Floer conjecture
The Atiyah–Floer conjecture connects the instanton Floer homology with the Lagrangian intersection Floer homology: Consider a 3-manifold Y with a Heegaard splittingHeegaard splitting
In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.-Definitions:...
along a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
. Then the space of flat connections on modulo gauge equivalence is a symplectic manifold of dimension 6g − 6, where g is the genusGenus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
of the surface
. In the Heegaard splitting, bounds two different 3-manifolds; the space of flat connections modulo gauge equivalence on each 3-manifold with boundary (equivalently, the space of connections on that extend over each three manifold) is a Lagrangian submanifold of the space of connections on . We may thus consider their Lagrangian intersection Floer homology. Alternately, we can consider the Instanton Floer homology of the 3-manifold Y. The Atiyah-Floer conjecture asserts that these two invariants are isomorphic. Katrin WehrheimKatrin Wehrheim
Katrin Wehrheim is Assistant Professor of Mathematics in the MIT Mathematics Department. Her research centers around symplectic topology and gauge theory.-Early life:...
and Dietmar Salamon are working on a program to prove this conjecture.
Relations to mirror symmetry
The homological mirror symmetryHomological mirror symmetry
Homological mirror symmetry is a mathematical conjecture made by Maxim Kontsevich. It seeks a systematic mathematical explanation for a phenomenon called mirror symmetry first observed by physicists studying string theory.-History:...
conjecture of Maxim Kontsevich
Maxim Kontsevich
Maxim Lvovich Kontsevich is a Russian mathematician. He is a professor at the Institut des Hautes Études Scientifiques and a distinguished professor at the University of Miami...
predicts an equality between the Lagrangian Floer homology of Lagrangians in a Calabi–Yau manifold
and the Ext groups of coherent sheaves on the mirror Calabi–Yau manifold. In this situation, one should not focus on the Floer homology groups but on the Floer chain groups. Similar to the pair-of-pants product, one can construct multi-compositions using pseudo-holomorphic n-gons. These compositions satisfy the 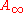-relations making the category of all (unobstructed) Lagrangian submanifolds in a symplectic manifold into an 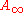-category, called the Fukaya category.To be more precise, one must add additional data to the Lagrangian – a grading and a spin structure
Spin structure
In differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
. A Lagrangian with a choice of these structures is often called a brane in homage to the underlying physics. The Homological Mirror Symmetry conjecture states there is a type of derived Morita equivalence
Morita equivalence
In abstract algebra, Morita equivalence is a relationship defined between rings that preserves many ring-theoretic properties. It is named after Japanese mathematician Kiiti Morita who defined equivalence and a similar notion of duality in 1958.- Motivation :...
between the Fukaya category of the Calabi–Yau
and a dg category underlying the bounded derived categoryDerived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of coherent sheaves of the mirror, and vice-versa.
Symplectic field theory (SFT)
This is an invariant of contact manifolds and symplectic cobordismCobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
s between them, originally due to Yakov Eliashberg
Yakov Eliashberg
Yakov Eliashberg is a Russian mathematician. He received his Ph.D. from Leningrad University in 1972 under the direction of Vladimir Rokhlin. From 1972 to 1979 he taught at the Syktyvkar State University of Komi Republic of Russia and from 1980 to 1987 worked in industry as the head of a computer...
, Alexander Givental
Alexander Givental
Alexander Givental is a Russian American mathematician working in the area of symplectic topology, singularity theory and their relations to topological string theories. He got his Ph. D. under the supervision of V. I. Arnold. He, first, proved the mirror conjecture for toric Calabi-Yau manifolds,...
and Helmut Hofer. The symplectic field theory as well as its subcomplexes, rational symplectic field theory and contact homology, are defined as homologies of differential algebras, which are generated by closed orbits of the Reeb vector field
Reeb vector field
In mathematics, the Reeb vector field, named after the French mathematician Georges Reeb, is a notion that appears in various domains of contact geometry including:...
of a chosen contact form. The differential counts certain holomorphic curves in the cylinder over the contact manifold, where the trivial examples are the branched coverings of (trivial) cylinders over closed Reeb orbits. It further includes a linear homology theory, called cylindrical or linearized contact homology (sometimes, by abuse of notation, just contact homology), whose chain groups are vector spaces generated by closed orbits and whose differentials count only holomorphic cylinders. However, cylindrical contact homology is not always defined due to the presence of holomorphic discs. In situations where cylindrical contact homology makes sense, it may be seen as the (slightly modified) "Morse homology" of the action functional on the free loop space which sends a loop to the integral of the contact form alpha over the loop. Reeb orbits are the critical points of this functional.
SFT also associates a relative invariant of a Legendrian submanifold of a contact manifold known as relative contact homology
Relative contact homology
In mathematics, in the area of symplectic topology, relative contact homology is an invariant of spaces together with a chosen subspace. Namely, it is associated to a contact manifold and one of its Legendrian submanifolds...
.
In SFT the contact manifolds can be replaced by mapping tori
Mapping torus
In mathematics, the mapping torus in topology of a homeomorphism f of some topological space X to itself is a particular geometric construction with f...
of symplectic manifolds with symplectomorphisms. While the cylindrical contact homology is well-defined and given by the symplectic Floer homologies of powers of the symplectomorphism, (rational) symplectic field theory and contact homology can be considered as generalized symplectic Floer homologies. In the important case when the symplectomorphism is the time-one map of a time-dependent Hamiltonian, it was however shown that these higher invariants do not contain any further information.
Floer homotopy
One conceivable way to construct a Floer homology theory of some object would be to construct a related spectrumSpectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
whose ordinary homology is the desired Floer homology. Applying other homology theories to such a spectrum could yield other interesting invariants. This strategy was proposed by Ralph Cohen, John Jones, and Graeme Segal
Graeme Segal
Graeme Bryce Segal is a British mathematician, and professor at the University of Oxford.Segal was educated at the University of Sydney, where he received his BSc degree in 1961. He went on to receive his D.Phil...
, and carried out in certain cases for Seiberg–Witten–Floer homology by Kronheimer and Manolescu and for the symplectic Floer homology of cotangent bundles by Cohen.
Analytic foundations
Many of these Floer homologies have not been completely and rigorously constructed, and many conjectural equivalences have not been proved. Technical difficulties come up in the analysis involved, especially in constructing compactifiedCompactification
Compactification may refer to:* Compactification , making a topological space compact* Compactification , the "curling up" of extra dimensions in string theory* Compaction...
moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
s of pseudoholomorphic curves. Hofer, in collaboration with Kris Wysocki and Eduard Zehnder, has developed new analytic foundations via their theory of polyfolds and a "general Fredholm theory". While the polyfold project is not yet fully completed, in some important cases transversality was shown using simpler methods.
Computation
Floer homologies are generally difficult to compute explicitly. For instance, the symplectic Floer homology for all surface symplectomorphisms was completed only in 2007. The Heegaard Floer homology has been huge success story in this regard: researchers have exploited its algebraic structure to compute it for various classes of 3-manifolds and indeed found combinatorial algorithms for computationof much of the theory. It is also connected it to existing invariants and structures and many insights into 3-manifold topology have resulted.
Books and surveys
- Michael AtiyahMichael AtiyahSir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
, New invariants of 3- and 4-dimensional manifolds. The mathematical heritage of Hermann Weyl (Durham, NC, 1987), 285–299, Proc. Sympos. Pure Math., 48, Amer. Math. Soc., Providence, RI, 1988. - Augustin BanyagaAugustin BanyagaAugustin Banyaga is a Rwandan-born American mathematician whose research fields include symplectic topology and contact geometry. He is currently a Professor of Mathematics at Pennsylvania State University.-Biography:...
and David Hurtubise (2004). Lectures on Morse Homology. Dordrecht: Kluwer Academic Publishers. ISBN 1-4020-2695-1. Floer homology in this book - Simon DonaldsonSimon DonaldsonSimon Kirwan Donaldson FRS , is an English mathematician known for his work on the topology of smooth four-dimensional manifolds. He is now Royal Society research professor in Pure Mathematics and President of the Institute for Mathematical Science at Imperial College London...
, with the assistance of M. Furuta and D. Kotschick (2002). Floer homology groups in Yang-Mills theory. (Cambridge tracts in mathematics; 147) Cambridge University PressCambridge University PressCambridge University Press is the publishing business of the University of Cambridge. Granted letters patent by Henry VIII in 1534, it is the world's oldest publishing house, and the second largest university press in the world...
. ISBN 0-521-80803-0. - David A. Ellwood (Editor), Peter S. Ozsvath (Editor), Andras I. Stipsicz (Editor), Zoltan Szabo (Editor).(2006). Floer Homology, Gauge Theory, And Low-dimensional Topology Proceedings of the Clay Mathematics InstituteClay Mathematics InstituteThe Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
2004 Summer School, Alfred Renyi Institute of ... 2004 (Clay Mathematics Proceedings, V. 5) (Paperback), ISBN 0-8218-3845-8 - Dusa McDuffDusa McDuffDusa McDuff is an English mathematician. She was born in London, England as the daughter of the noted biologist Conrad Hal Waddington. Her mother, Justin, born Justin Blanco White, was an architect, while her maternal grandmother was the feminist Amber Reeves, a lover of H.G. Wells and an author...
and Dietmar Salamon (1998). Introduction to Symplectic Topology. Oxford Mathematical Monographs, ISBN 0-19-850451-9. Floer homology in this book - Dusa McDuffDusa McDuffDusa McDuff is an English mathematician. She was born in London, England as the daughter of the noted biologist Conrad Hal Waddington. Her mother, Justin, born Justin Blanco White, was an architect, while her maternal grandmother was the feminist Amber Reeves, a lover of H.G. Wells and an author...
(2005). Floer theory and low dimensional topology. Bulletin of the American Mathematical Society 43 (2006), 25–42.Preprint from McDuff's homepage - Matthias Schwarz, Morse Homology. Birkhäuser, 1993.
Research articles
- Andreas FloerAndreas FloerAndreas Floer was a German mathematician who made seminal contributions to the areas of geometry, topology, and mathematical physics, in particular the invention of Floer homology.-Life:...
, The unregularized gradient flow of the symplectic action, Comm. Pure Appl. Math.Communications on Pure and Applied MathematicsCommunications on Pure and Applied Mathematics is a scientific journal which is associated with the Courant Institute of Mathematical Sciences. It publishes original research originating from or solicited by the institute, typically in the fields of applied mathematics, mathematical analysis, or...
41 (1988), 775–813. - Floer, Andreas, An instanton-invariant for 3-manifolds, Comm. Math. Phys. 118 (1988), no. 2, 215–240. Project Euclid
- Floer, Andreas, Morse theory for Lagrangian intersections, J. Differential Geom. 28 (1988), no. 3, 513–547.
- Floer, Andreas, Cuplength estimates on Lagrangian intersections, Comm. Pure Appl. Math.Communications on Pure and Applied MathematicsCommunications on Pure and Applied Mathematics is a scientific journal which is associated with the Courant Institute of Mathematical Sciences. It publishes original research originating from or solicited by the institute, typically in the fields of applied mathematics, mathematical analysis, or...
42 (1989), no. 4, 335–356. - Floer, Andreas, Symplectic fixed points and holomorphic spheres. Comm. Math. Phys. 120, no. 4 (1989), 575–611.
- Floer, Andreas, “Witten's complex and infinite dimensional Morse Theory”. J. Diff. Geom. 30 (1989), p. 202–221.
- Mikhail Gromov, Pseudo holomorphic curves in symplectic manifolds, Inventiones MathematicaeInventiones MathematicaeInventiones Mathematicae, often just referred to as Inventiones, is a mathematical journal published monthly by Springer Verlag. It was founded in 1966.-Editors:...
(1985), vol. 82 no. 2, 307–347. - Helmut Hofer, Kris Wysocki, Eduard Zehnder, "A General Fredholm Theory I: A Splicing-Based Differential Geometry" J. Eur. Math. Soc. (JEMS) 9, No. 4, 841–876 (2007). http://arxiv.org/abs/math.FA/0612604
- Peter OzsváthPeter OzsváthPeter Steven Ozsváth is a professor of mathematics at Princeton University. He created, along with Zoltán Szabó, Heegaard Floer homology, a homology theory for 3-manifolds....
, Zoltán SzabóZoltán SzabóZoltán Szabó is a professor of mathematics at Princeton University. He created, along with Peter Ozsváth, Heegaard Floer homology, a homology theory for 3-manifolds. For this contribution to the field of topology, Ozsváth and Szabó were awarded the 2007 Oswald Veblen Prize in Geometry.He got his...
, On the Heegaard Floer homology of branched double-covers, Adv. Math. 194 (2005), no. 1, 1–33. Also available as a preprint.