Fukaya category
Encyclopedia
In symplectic topology
, a discipline within mathematics, a Fukaya category of a symplectic manifold
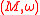is a category
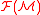whose objects are Lagrangian submanifolds of 
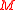, and morphism
s are Floer chain groups
:
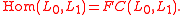. Its finer structure can be described in the language of quasi categories
as an A∞-category.
They are named after Kenji Fukaya who introduced the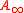
language first in the context of Morse homology
, and exist in a number of variants. As Fukaya categories are A∞-categories, they have associated derived categories, which are the subject of a celebrated conjecture of Maxim Kontsevich
: the homological mirror symmetry
. This conjecture has been verified by computations for a variety of comparatively simple examples.
Symplectic topology
Symplectic geometry is a branch of differential geometry and differential topology which studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form...
, a discipline within mathematics, a Fukaya category of a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
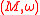is a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
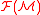whose objects are Lagrangian submanifolds of 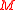, and morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s are Floer chain groups
Floer homology
Floer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology. First introduced by Andreas Floer in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory arising as an infinite dimensional analog of finite...
:
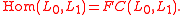. Its finer structure can be described in the language of quasi categoriesQuasi-category
In mathematics, a quasi-category is a higher categorical generalization of a notion of a category introduced by .André Joyal has much advanced the study of quasi-categories showing that most of the usual basic category...
as an A∞-category.
They are named after Kenji Fukaya who introduced the
language first in the context of Morse homologyMorse homology
In mathematics, specifically in the field of differential topology, Morse homology is a homology theory defined for any smooth manifold. It is constructed using the smooth structure and an auxiliary metric on the manifold, but turns out to be topologically invariant, and is in fact isomorphic to...
, and exist in a number of variants. As Fukaya categories are A∞-categories, they have associated derived categories, which are the subject of a celebrated conjecture of Maxim Kontsevich
Maxim Kontsevich
Maxim Lvovich Kontsevich is a Russian mathematician. He is a professor at the Institut des Hautes Études Scientifiques and a distinguished professor at the University of Miami...
: the homological mirror symmetry
Homological mirror symmetry
Homological mirror symmetry is a mathematical conjecture made by Maxim Kontsevich. It seeks a systematic mathematical explanation for a phenomenon called mirror symmetry first observed by physicists studying string theory.-History:...
. This conjecture has been verified by computations for a variety of comparatively simple examples.