Discrete Morse theory
Encyclopedia
Discrete Morse theory is a combinatorial adaptation of Morse theory
defined on finite CW complex
es.
be a CW complex
. Define the incidence function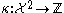
in the following way: given two cells 
and 
in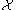 
, 
equals the degree
of the attaching map from the boundary of
to 
. The boundary operator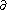 
on 
is defined by
It is a defining property of boundary operators that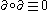
.
-valued function
is a discrete Morse function if it satisfies the following two properties:
It can be shown that both conditions can not hold simultaneously for a fixed cell
provided that 
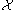is a regular CW complex. In this case, each cell 
can be paired with at most one exceptional cell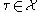 
: either a boundary cell with larger 
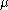value, or a co-boundary cell with smaller 
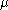value. The cells which have no pairs, i.e., their function values are strictly higher than their boundary cells and strictly lower than their co-boundary cells are called critical cells. Thus, a discrete Morse function partitions the CW complex into three distinct cell collections: 
, where:
By construction, there is a bijection
of sets between
-dimensional cells in 
and the 
-dimensional cells in 
, which can be denoted by 
for each natural number
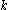. It is an additional technical requirement that for each 
, the degree of the attaching map from the boundary of 
to its paired cell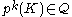 
is a unit
in the underlying ring
of
. For instance, over the integers
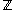, the only allowed values are 
. This technical requirement is guaranteed when one assumes that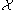 
is a regular CW complex over 
.
The fundamental result of discrete Morse theory establishes that the CW complex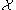
is isomorphic
on the level of homology
to a new complex
consisting of only the critical cells. The paired cells in 
and 
describe gradient paths between adjacent critical cells which can be used to obtain the boundary operator on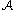 
. Some details of this construction are provided in the next section.
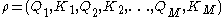is a sequence of cell pairs 
so that 
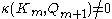. The index of this gradient path is defined to be the integer 
. The division here makes sense because the incidence between paired cells must be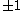 
. Note that by construction, the values of the discrete Morse function 
must decrease across 
. The path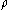 
is said to connect two critical cells 
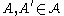if 
. This relationship may be expressed as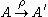 
. The multiplicity of this connection is defined to be the integer 
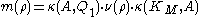. Finally, the Morse boundary operator on the critical cells 
is defined by
where the sum is taken over all gradient path connections from
to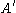 
.
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
defined on finite CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es.
Notation regarding CW complexes
Let be a CW complexCW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
. Define the incidence function
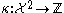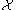in the following way: given two cells and in , equals the degreeTopological degree theory
In mathematics, topological degree theory is a generalization of the winding number of a curve in the complex plane. It can be used to estimate the number of solutions of an equation, and is closely connected to fixed-point theory. When one solution of an equation is easily found, degree theory can...
of the attaching map from the boundary of
to . The boundary operator 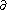on is defined byIt is a defining property of boundary operators that
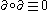.Discrete Morse functions
A RealReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued function
is a discrete Morse function if it satisfies the following two properties:- For any cell
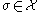, the number of cells 
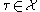in the boundary of 
which satisfy 
is at most one. - For any cell
, the number of cells 
containing 
in their boundary which satisfy 
is at most one.
It can be shown that both conditions can not hold simultaneously for a fixed cell
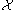provided that is a regular CW complex. In this case, each cell can be paired with at most one exceptional cell 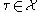: either a boundary cell with larger 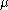value, or a co-boundary cell with smaller 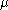value. The cells which have no pairs, i.e., their function values are strictly higher than their boundary cells and strictly lower than their co-boundary cells are called critical cells. Thus, a discrete Morse function partitions the CW complex into three distinct cell collections: , where:-
denotes the critical cells which are unpaired, -
denotes cells which are paired with boundary cells, and -
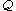denotes cells which are paired with co-boundary cells.
By construction, there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
of sets between
-dimensional cells in and the -dimensional cells in , which can be denoted by for each natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
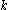. It is an additional technical requirement that for each , the degree of the attaching map from the boundary of to its paired cell 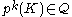is a unitUnit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in the underlying ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of
. For instance, over the integersInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
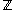, the only allowed values are . This technical requirement is guaranteed when one assumes that 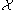is a regular CW complex over .The fundamental result of discrete Morse theory establishes that the CW complex
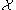is isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
on the level of homology
Homology
Homology may refer to:* Homology , analogy between human beliefs, practices or artifacts owing to genetic or historical connections* Homology , any characteristic of biological organisms that is derived from a common ancestor....
to a new complex
consisting of only the critical cells. The paired cells in and describe gradient paths between adjacent critical cells which can be used to obtain the boundary operator on 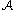. Some details of this construction are provided in the next section.The Morse complex
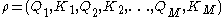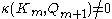A gradient path is a sequence of cell pairs so that . The index of this gradient path is defined to be the integer . The division here makes sense because the incidence between paired cells must be 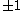. Note that by construction, the values of the discrete Morse function must decrease across . The path 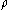is said to connect two critical cells if . This relationship may be expressed as 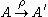. The multiplicity of this connection is defined to be the integer 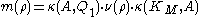. Finally, the Morse boundary operator on the critical cells is defined bywhere the sum is taken over all gradient path connections from
to 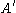.See also
- Digital Morse theoryDigital Morse theoryIn mathematics, digital Morse theory is a digital adaptation of continuum Morse theory for scalar volume data.The main utility of a digital Morse theory is that it serves to provide a theoretical basis for isosurfaces, and perpendicular streamlines....
- Stratified Morse theory
- Piece-wise linear Morse theory
- Shape analysisShape analysisThis article describes shape analysis to analyze and process geometric shapes.The shape analysis described here is related to the statistical analysis of geometric shapes, to shape matching and shape recognition...
- Topological combinatoricsTopological combinatoricsThe discipline of combinatorial topology used combinatorial concepts in topology and in the early 20th century this gradually turned into the field of algebraic topology....
- Discrete differential geometryDiscrete differential geometryDiscrete differential geometry is the study of discrete counterparts of notions in differential geometry. Instead of smooth curves and surfaces, there are polygons, meshes, and simplicial complexes...