
Stratified Morse theory
Encyclopedia
In mathematics, stratified Morse theory is an analogue to Morse theory
for general stratified spaces
, originally developed by Mark Goresky
and Robert MacPherson. The main point of the theory is to consider functions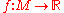 and consider how the stratified space
and consider how the stratified space 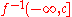 changes as the real number
changes as the real number 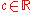 changes. Morse theory of stratified spaces has uses everywhere from pure mathematics topics such as braid groups and representations to robot motion planning and potential theory. A popular application in pure mathematics is Morse theory on manifolds with boundary, and manifolds with corners.
changes. Morse theory of stratified spaces has uses everywhere from pure mathematics topics such as braid groups and representations to robot motion planning and potential theory. A popular application in pure mathematics is Morse theory on manifolds with boundary, and manifolds with corners.
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
for general stratified spaces
Topologically stratified space
In topology, a branch of mathematics, a topologically stratified space is a space X that has been decomposed into pieces called strata; these strata are topological manifolds and are required to fit together in a certain way...
, originally developed by Mark Goresky
Mark Goresky
Robert Mark Goresky is a Canadian mathematician who invented intersection homology with Robert MacPherson.He received his Ph.D. from Brown University in 1976. His thesis, titled Geometric Cohomology and Homology of Stratified Objects, was written under the direction of MacPherson...
and Robert MacPherson. The main point of the theory is to consider functions
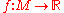 and consider how the stratified space
and consider how the stratified space 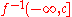 changes as the real number
changes as the real number 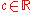 changes. Morse theory of stratified spaces has uses everywhere from pure mathematics topics such as braid groups and representations to robot motion planning and potential theory. A popular application in pure mathematics is Morse theory on manifolds with boundary, and manifolds with corners.
changes. Morse theory of stratified spaces has uses everywhere from pure mathematics topics such as braid groups and representations to robot motion planning and potential theory. A popular application in pure mathematics is Morse theory on manifolds with boundary, and manifolds with corners.See also
- Digital Morse theoryDigital Morse theoryIn mathematics, digital Morse theory is a digital adaptation of continuum Morse theory for scalar volume data.The main utility of a digital Morse theory is that it serves to provide a theoretical basis for isosurfaces, and perpendicular streamlines....
- Discrete Morse theory
- Morse theoryMorse theoryIn differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
- Level set methodLevel set methodThe level set method is a numerical technique for tracking interfaces and shapes. The advantage of the level set method is that one can perform numerical computations involving curves and surfaces on a fixed Cartesian grid without having to parameterize these objects...

