Topologically stratified space
Encyclopedia
In topology
, a branch of mathematics, a topologically stratified space is a space X that has been decomposed into pieces called strata; these strata are topological manifolds and are required to fit together in a certain way. Topologically stratified spaces provide a purely topological setting for the study of singularities analogous to the more differential-geometric theory of Whitney
. They were introduced by René Thom
, who showed that every Whitney stratified space
was also a topologically stratified space, with the same strata. Another proof was given by John Mather
in 1970, inspired by Thom's proof.
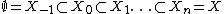
of X by closed subspaces such that for each i and for each point x of
there exists a neighborhood
of x in X, a compact n-i-1-dimensional stratified space L, and a filtration-preserving homeomorphism
.
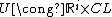Here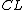
is the open cone
on L.
If X is a topologically stratified space, the i-dimensional stratum of X is the space
Connected components of Xi \ Xi-1 are also frequently called strata.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a branch of mathematics, a topologically stratified space is a space X that has been decomposed into pieces called strata; these strata are topological manifolds and are required to fit together in a certain way. Topologically stratified spaces provide a purely topological setting for the study of singularities analogous to the more differential-geometric theory of Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
. They were introduced by René Thom
René Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
, who showed that every Whitney stratified space
Whitney conditions
In differential topology, a branch of mathematics, the Whitney conditions are conditions on a pair of submanifolds of a manifold introduced by Hassler Whitney in 1965...
was also a topologically stratified space, with the same strata. Another proof was given by John Mather
John Mather
John Norman Mather is a mathematician at Princeton University known for his work on singularity theory and Hamiltonian dynamics...
in 1970, inspired by Thom's proof.
Definition
The definition is inductive on the dimension of X. An n-dimensional topological stratification of X is a filtration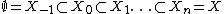of X by closed subspaces such that for each i and for each point x of
- Xi \ Xi-1,
there exists a neighborhood
of x in X, a compact n-i-1-dimensional stratified space L, and a filtration-preserving homeomorphism
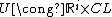.Here
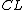is the open coneCone (topology)
In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:CX = /\,of the product of X with the unit interval I = [0, 1]....
on L.
If X is a topologically stratified space, the i-dimensional stratum of X is the space
- Xi \ Xi-1.
Connected components of Xi \ Xi-1 are also frequently called strata.
See also
- Singularity theorySingularity theory-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
- Whitney conditionsWhitney conditionsIn differential topology, a branch of mathematics, the Whitney conditions are conditions on a pair of submanifolds of a manifold introduced by Hassler Whitney in 1965...
- Thom-Mather stratified space
- StratifoldStratifoldIn differential topology, a branch of mathematics, a stratifold is a generalization of a differentiable manifold where certain kinds of singularities are allowed. More specifically a stratifold is stratified into differentiable manifolds of different dimensions. Stratifolds can be used to...
- Intersection homology