
Gradient-like vector field
Encyclopedia
In differential topology
, a mathematical discipline, and more specifically in Morse theory
, a gradient-like vector field is a generalization of gradient vector field.
The primary motivation is as a technical tool in the construction of Morse functions, to show that one can construct a function whose critical points are at distinct levels. One first constructs a Morse function, then uses gradient-like vector fields to move around the critical points, yielding a different Morse function.
Formally:
and on which X equals the gradient of f.
of a gradient-like vector field, a gradient-like dynamical system, is a special case of a Morse–Smale system
.
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, a mathematical discipline, and more specifically in Morse theory
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
, a gradient-like vector field is a generalization of gradient vector field.
The primary motivation is as a technical tool in the construction of Morse functions, to show that one can construct a function whose critical points are at distinct levels. One first constructs a Morse function, then uses gradient-like vector fields to move around the critical points, yielding a different Morse function.
Definition
Given a Morse function f on a manifold M, a gradient-like vector field X for the function f is, informally:- away from critical points, X points "in the same direction as" the gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of f, and - near a critical point (in the neighborhood of a critical point), it equals the gradient of f, when f is written in standard form given in the Morse lemmas.
Formally:
- away from critical points,

- around every critical point there is a neighborhood on which f is given as in the Morse lemmas:
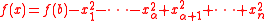
and on which X equals the gradient of f.
Dynamical system
The associated dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
of a gradient-like vector field, a gradient-like dynamical system, is a special case of a Morse–Smale system
Morse–Smale system
In dynamical systems theory, an area of applied mathematics, a Morse–Smale system is a smooth dynamical system whose non-wandering set consists of finitely many hyperbolic equilibrium points and hyperbolic periodic orbits and satisfying a transversality condition on the stable and unstable manifolds...
.

