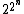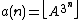
Double exponential function
Encyclopedia
A double exponential function is a constant
raised to the power of an exponential function
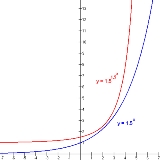
. The general formula is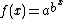 , which grows much more quickly than an exponential function. For example, if a = b = 10:
, which grows much more quickly than an exponential function. For example, if a = b = 10:
Factorial
s grow faster than exponential functions, but much slower than double-exponential functions. The hyper-exponential function
and Ackermann function
grow even faster. See Big O notation
for a comparison of the rate of growth of various functions.
The inverse of a double exponential function is a double logarithm.
s, each term is a constant plus the square of the previous term, and show that such sequences can be formed by rounding to the nearest integer the values of a doubly exponential function in which the middle exponent is two. Integer sequences with this squaring behavior include
More generally, if the nth value of an integer sequences is proportional to a double exponential function of n, Ionascu and Stanica call the sequence "almost doubly-exponential" and describe conditions under which it can be defined as the floor of a doubly-exponential sequence plus a constant. Additional sequences of this type include
, some algorithms take double-exponential time:
bounds are double exponential. Odd perfect numbers with n distinct prime factors are known to be at most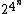
a result of Nielsen (2003).
The largest known prime number in the electronic era has grown roughly as a double exponential function of the year since Miller
and Wheeler found a 79-digit prime on EDSAC
1 in 1951.
the growth of human population is sometimes supposed to be double exponential. Gurevich and Varfolomeyev experimentally fit
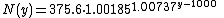
where N(y) is the population in year y in millions.
, the logarithm of amplitude varies exponentially with time (for large amplitudes), thus the amplitude varies as double-exponential function of time.
Constant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
raised to the power of an exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
. The general formula is
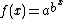 , which grows much more quickly than an exponential function. For example, if a = b = 10:
, which grows much more quickly than an exponential function. For example, if a = b = 10:
- f(−1) ≈ 1.26
- f(0) = 10
- f(1) = 1010
- f(2) = 10100 = googolGoogolA googol is the large number 10100, that is, the digit 1 followed by 100 zeros:The term was coined in 1938 by 9-year-old Milton Sirotta , nephew of American mathematician Edward Kasner...
- f(3) = 101000
- f(100) = 1010100 = googolplex.
Factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s grow faster than exponential functions, but much slower than double-exponential functions. The hyper-exponential function
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
and Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
grow even faster. See Big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
for a comparison of the rate of growth of various functions.
The inverse of a double exponential function is a double logarithm.
Doubly exponential sequences
Aho and Sloane observed that in several important integer sequenceInteger sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
s, each term is a constant plus the square of the previous term, and show that such sequences can be formed by rounding to the nearest integer the values of a doubly exponential function in which the middle exponent is two. Integer sequences with this squaring behavior include
- The Fermat numbers
-
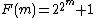
- The harmonic primes: The primes p, in which the sequence 1/2+1/3+1/5+1/7+....+1/p exceeds 0,1,2,3,....
- The first few numbers, starting with 0, are 2,5,277,5195977,...
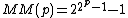
- The elements of Sylvester's sequenceSylvester's sequenceIn number theory, Sylvester's sequence is an integer sequence in which each member of the sequence is the product of the previous members, plus one. The first few terms of the sequence are:...
- The elements of Sylvester's sequence
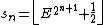
- where E ≈ 1.264084735305 is Vardi's constant.
- The number of k-aryArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
operatorsLogical connectiveIn logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
:
- The number of k-ary
More generally, if the nth value of an integer sequences is proportional to a double exponential function of n, Ionascu and Stanica call the sequence "almost doubly-exponential" and describe conditions under which it can be defined as the floor of a doubly-exponential sequence plus a constant. Additional sequences of this type include
- The prime numbers 2, 11, 1361, ...
-
- where A ≈ 1.306377883863 is Mills' constant.
Algorithmic complexity
In computational complexity theoryComputational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, some algorithms take double-exponential time:
- Decision procedures for Presburger arithmeticPresburger arithmeticPresburger arithmetic is the first-order theory of the natural numbers with addition, named in honor of Mojżesz Presburger, who introduced it in 1929. The signature of Presburger arithmetic contains only the addition operation and equality, omitting the multiplication operation entirely...
- Computing a Gröbner basisGröbner basisIn computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
- Finding a complete set of associative-commutative unifiers
- Satisfying CTL+ (which is, in fact, 2-EXPTIME2-EXPTIMEIn computational complexity theory, the complexity class 2-EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
-complete) - Quantifier eliminationQuantifier eliminationQuantifier elimination is a concept of simplification used in mathematical logic, model theory, and theoretical computer science. One way of classifying formulas is by the amount of quantification...
on real closed fieldReal closed fieldIn mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
s takes at least doubly-exponential time (but is not even known to be computable in ELEMENTARY) - Calculating the complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of a regular expressionRegular expressionIn computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
Number theory
Some number theoreticalNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
bounds are double exponential. Odd perfect numbers with n distinct prime factors are known to be at most
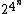
a result of Nielsen (2003).
The largest known prime number in the electronic era has grown roughly as a double exponential function of the year since Miller
J. C. P. Miller
Jeffrey Charles Percy Miller was an English mathematician and computing pioneer. He worked in number theory and on geometry, particularly polyhedra, where Miller's monster refers to the great dirhombicosidodecahedron....
and Wheeler found a 79-digit prime on EDSAC
EDSAC
Electronic Delay Storage Automatic Calculator was an early British computer. The machine, having been inspired by John von Neumann's seminal First Draft of a Report on the EDVAC, was constructed by Maurice Wilkes and his team at the University of Cambridge Mathematical Laboratory in England...
1 in 1951.
Theoretical biology
In population dynamicsPopulation dynamics
Population dynamics is the branch of life sciences that studies short-term and long-term changes in the size and age composition of populations, and the biological and environmental processes influencing those changes...
the growth of human population is sometimes supposed to be double exponential. Gurevich and Varfolomeyev experimentally fit
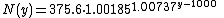
where N(y) is the population in year y in millions.
Physics
In the Toda oscillator model of self-pulsationSelf-pulsation
Self-pulsation takes place at the beginning of laser action.As the pump is switched on, the gainin the active medium rises and exceeds the steady-state value...
, the logarithm of amplitude varies exponentially with time (for large amplitudes), thus the amplitude varies as double-exponential function of time.