Doxastic logic - AbsoluteAstronomy.com

Doxastic logic is a modal logic

Modal logic

Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...

concerned with reasoning about belief

Belief

Belief is the psychological state in which an individual holds a proposition or premise to be true.-Belief, knowledge and epistemology:The terms belief and knowledge are used differently in philosophy....

s. The term doxastic derives from the ancient Greek

Ancient Greek

Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...

δόξα, doxa
Doxa
Doxa is a Greek word meaning common belief or popular opinion, from which are derived the modern terms of orthodoxy and heterodoxy.Used by the Greek rhetoricians as a tool for the formation of argument by using common opinions, the doxa was often manipulated by sophists to persuade the people,...

, which means "belief." Typically, a doxastic logic uses 'Bx' to mean "It is believed that x is the case," and the set

denotes

Denotation

This word has distinct meanings in other fields: see denotation . For the opposite of Denotation see Connotation.*In logic, linguistics and semiotics, the denotation of a word or phrase is a part of its meaning; however, the part referred to varies by context:** In grammar and literary theory, the...

a set of beliefs

Theory (mathematical logic)

In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...

. In doxastic logic, belief is treated as a modal operator

Modal operator

In modal logic, a modal operator is an operator which forms propositions from propositions. In general, a modal operator has the "formal" property of being non-truth-functional, and is "intuitively" characterised by expressing a modal attitude about the proposition to which the operator is applied...

: {

}

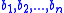There is complete parallelism between a person who believes proposition

Proposition

In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...

s and a formal system

Formal system

In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...

that derives

Formal proof

A formal proof or derivation is a finite sequence of sentences each of which is an axiom or follows from the preceding sentences in the sequence by a rule of inference. The last sentence in the sequence is a theorem of a formal system...

propositions. Using doxastic logic, one can express the epistemic

Epistemic logic

Epistemic modal logic is a subfield of modal logic that is concerned with reasoning about knowledge. While epistemology has a long philosophical tradition dating back to Ancient Greece, epistemic logic is a much more recent development with applications in many fields, including philosophy,...

counterpart of Gödel's incompleteness theorem of metalogic

Metalogic

Metalogic is the study of the metatheory of logic. While logic is the study of the manner in which logical systems can be used to decide the correctness of arguments, metalogic studies the properties of the logical systems themselves...

, as well as Löb's theorem

Löb's theorem

In mathematical logic, Löb's theorem states that in a theory with Peano arithmetic, for any formula P, if it is provable that "if P is provable then P", then P is provable...

, and other metalogical results in terms of belief.

Types of reasoners

To demonstrate the properties of sets of beliefs, Raymond Smullyan defines the following types of reasoners:

Accurate reasoner:

An accurate reasoner never believes any false proposition. (modal axiom T)

p(Bpp)

Inaccurate reasoner: An inaccurate reasoner believes at least one false proposition.

p(Bpp)

Conceited reasoner: A conceited reasoner believes his or her beliefs are never inaccurate. A conceited reasoner will necessarily lapse into an inaccuracy.

B(p(Bpp))

Consistent reasoner: A consistent reasoner never simultaneously believes a proposition and its negation. (modal axiom D)

p((BpBp))

Normal reasoner: A normal reasoner is one who, while believing p, also believes he or she believes p (modal axiom 4).

p(BpBBp)

Peculiar reasoner: A peculiar reasoner believes proposition p while also believing he or she does not believe p. Although a peculiar reasoner may seem like a strange psychological phenomenon (see Moore's paradox
Moore's paradox
Moore's paradox concerns the putative absurdity involved in asserting a first-person present-tense sentence such as 'It's raining but I don't believe that it is raining' or 'It's raining but I believe that it is not raining'. The first author to note this apparent absurdity was G.E. Moore...

), a peculiar reasoner is necessarily inaccurate but not necessarily inconsistent.

p(BpBBp)

Regular reasoner: A regular reasoner is one for whom all beliefs are distributive over logical operations. (modal axiom K)

p(q(B(pq)(BpBq)))

Reflexive reasoner: A reflexive reasoner is one for whom every proposition p has some q such that the reasoner believes q≡(Bq→p). So if a reflexive reasoner of type 4 [see below] believes Bp→p, he or she will believe p. This is a parallelism of Löb's theorem
Löb's theorem
In mathematical logic, Löb's theorem states that in a theory with Peano arithmetic, for any formula P, if it is provable that "if P is provable then P", then P is provable...

for reasoners.

Unstable reasoner: An unstable reasoner is one for whom there is some proposition p such that he or she believes he or she believes p, but who does not really believe p. This is just as strange a psychological phenomenon as peculiarity; however, an unstable reasoner is not necessarily inconsistent.

Stable reasoner: A stable reasoner is not unstable. That is, for every p, if he or she believes Bp then he or she believes p. Note that stability is the converse of normality. We will say that a reasoner believes he or she is stable if for every proposition p, he or she believes BBp→Bp (believing: "If I should ever believe that I believe p, then I really will believe p").

BBpBp

Modest reasoner: A modest reasoner is one for whom every believed proposition p, 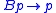only if he or she believes p. A modest reasoner never believes Bp→p unless he or she believes p. Any reflexive reasoner of type 4 is modest. (Löb's Theorem
Löb's theorem
In mathematical logic, Löb's theorem states that in a theory with Peano arithmetic, for any formula P, if it is provable that "if P is provable then P", then P is provable...

)

B(Bp→p)→Bp

Queer reasoner: A queer reasoner is of type G and believes he or she is inconsistent—but is wrong in this belief.

Timid reasoner: A timid reasoner is afraid to believe p [i.e., he or she does not believe p] if he or she believes

Increasing levels of rationality

Type 1 reasoner: A type 1 reasoner has a complete knowledge of propositional logic i.e., he or she sooner or later believes every tautology
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...

(any proposition provable by truth tables) (modal axiom N). Also, his or her set of beliefs (past, present and future) is logically closed
Deductive closure
Peter D. Klein, in the second edition of The Cambridge Dictionary of Philosophy, defines closure as follows:A set of objects, O, is said to exhibit closure or to be closed under a given operation, R, provided that for every object, x, if x is a member of O and x is R-related to any object, y, then...

under modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...

. If he or she ever believes p and believes p→q (p implies q) then he or she will (sooner or later) believe q (modal axiom K). This is equivalent to modal system K.

p Bp
(BpB(pq))Bq

Type 1* reasoner: A type 1* reasoner believes all tautologies; his or her set of beliefs (past, present and future) is logically closed under modus ponens, and for any propositions p and q, if he or she believes p→q, then he or she will believe that if he or she believes p then he or she will believe q. The type 1* reasoner has a shade more self awareness than a type 1 reasoner.

B(pq)B(BpBq)

Type 2 reasoner: A reasoner is of type 2 if he or she is of type 1, and if for every p and q he or she (correctly) believes: "If I should ever believe both p and p→q, then I will believe q." Being of type 1, he or she also believes the logically equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...

proposition: B(p→q)→(Bp→Bq). A type 2 reasoner knows his or her beliefs are closed under modus ponens.

B((BpB(pq))Bq)

Type 3 reasoner: A reasoner is of type 3 if he or she is a normal reasoner of type 2.

Type 4 reasoner: A reasoner is of type 4 if he or she is of type 3 and also believes he or she is normal.

Type G reasoner: A reasoner of type 4 who believes he or she is modest.

Gödel incompleteness and doxastic undecidability

Let us say an accurate reasoner is faced with the task of assigning a truth value to a statement posed to him or her. There exists a statement which the reasoner must either remain forever undecided about or lose his or her accuracy. One solution is the statement:

S: "I will never believe this statement."

If the reasoner ever believes the statement S, it becomes falsified by that fact, making S an untrue belief and hence making the reasoner inaccurate in believing S.

Therefore, since the reasoner is accurate, he or she will never believe S. Hence the statement was true, because that is exactly what it claimed. It further follows that the reasoner will never have the false belief that S is true. The reasoner cannot believe either that the statement is true or false without becoming inconsistent (i.e. holding two contradictory

Contradiction

In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...

beliefs). And so the reasoner must remain forever undecided as to whether the statement S is true or false.

The equivalent theorem is that for any formal system F, there exists a mathematical statement which can be interpreted as "This statement is not provable in formal system F". If the system F is consistent, neither the statement nor its opposite will be provable in it.

Inconsistency and peculiarity of conceited reasoners

A reasoner of type 1 is faced with the statement "I will never believe this sentence." The interesting thing now is that if the reasoner believes he or she is always accurate, then he or she will become inaccurate. Such a reasoner will reason: "If I believe the statement then it will be made false by that fact, which means that I will be inaccurate. This is impossible, since I'm always accurate. Therefore I can't believe the statement: it must be false."

At this point the reasoner believes that the statement is false, which makes the statement true. Thus the reasoner is inaccurate in believing that the statement is false. If the reasoner hadn't assumed his or her own accuracy, he or she would never have lapsed into an inaccuracy.

It can also be shown that a conceited reasoner is peculiar.

Self fulfilling beliefs

For systems, we define reflexivity to mean that for any p (in the language of the system) there is some q such that q≡(Bq→p) is provable in the system. Löb's theorem (in a general form) is that for any reflexive system of type 4, if Bp→p is provable in the system, so is p.

Inconsistency of the belief in one's stability

If a consistent reflexive reasoner of type 4 believes that he or she is stable, then he or she will become unstable. Stated otherwise, if a stable reflexive reasoner of type 4 believes that he or she is stable, then he or she will become inconsistent. Why is this? Suppose that a stable reflexive reasoner of type 4 believes that he or she is stable. We will show that he or she will (sooner or later) believe every proposition p (and hence be inconsistent). Take any proposition p. The reasoner believes BBp→Bp, hence by Löb's theorem he or she will believe Bp (because he or she believes Br→r, where r is the proposition Bp, and so he or she will believe r, which is the proposition Bp). Being stable, he or she will then believe p.