Drazin inverse
Encyclopedia
In mathematics
, the Drazin inverse, named after Michael P. Drazin
, is a kind of generalized inverse
of a matrix
.
Let A be a square matrix. The index
of A is the least nonnegative integer k such that rank(Ak+1) = rank(Ak). The Drazin inverse of A is the unique matrix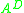
, which satisfies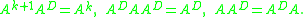
If A is invertible with inverse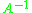
, then 
.
The Drazin inverse of a matrix of index 1 is called the group inverse or {1,2,5}-inverse and denoted A#.
A projection
P, as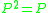
, has index 1 and 
.
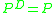If A is a nilpotent matrix
(for example a shift matrix
), then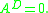
The hyper-power sequence is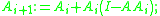
for convergence notice that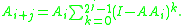 
For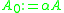
or any regular 
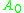with 
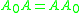chosen such that 
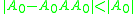the sequence tends to its Drazin inverse,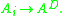
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Drazin inverse, named after Michael P. Drazin
Michael P. Drazin
Michael P. Drazin is American mathematician, working in noncommutative algebra.-See also:* *-regular semigroup* Drazin inverse-External links:*...
, is a kind of generalized inverse
Generalized inverse
In mathematics, a generalized inverse or pseudoinverse of a matrix A is a matrix that has some properties of the inverse matrix of A but not necessarily all of them...
of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
Let A be a square matrix. The index
Index (mathematics)
The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
of A is the least nonnegative integer k such that rank(Ak+1) = rank(Ak). The Drazin inverse of A is the unique matrix
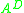, which satisfies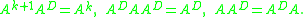If A is invertible with inverse
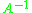, then .The Drazin inverse of a matrix of index 1 is called the group inverse or {1,2,5}-inverse and denoted A#.
A projection
Projection (linear algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
P, as
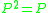, has index 1 and 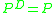.If A is a nilpotent matrix
Nilpotent matrix
In linear algebra, a nilpotent matrix is a square matrix N such thatN^k = 0\,for some positive integer k. The smallest such k is sometimes called the degree of N....
(for example a shift matrix
Shift matrix
In mathematics, a shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere. A shift matrix U with ones on the superdiagonal is an upper shift matrix....
), then
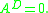
The hyper-power sequence is
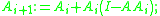for convergence notice that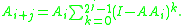 For
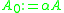or any regular 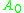with 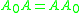chosen such that 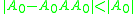the sequence tends to its Drazin inverse,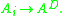See also
- Constrained generalized inverseConstrained generalized inverseA constrained generalized inverse inverse is obtained by solving a system of linear equations with an additional constraint that the solution is in a given subspace...
- Inverse elementInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
- Moore–Penrose inverse