
Du Val singularity
Encyclopedia
In algebraic geometry
, a du Val singularity, also called simple surface singularity, Kleinian singularity, or rational double point, is a singularity of a surface that is a double cover branched over a curve with an A-D-E singularity
. They are the canonical singularities in dimension 2. They were studied by and Felix Klein
.
The du Val singularities also appear as quotients of C2 by a finite subgroup of SL2(C); equivalently, a finite subgroup of SU(2), which are known as binary polyhedral groups. The rings of invariant polynomial
s of these finite group actions were computed by Klein, and are essentially the coordinate rings of the singularities; this is a classic result in invariant theory
.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a du Val singularity, also called simple surface singularity, Kleinian singularity, or rational double point, is a singularity of a surface that is a double cover branched over a curve with an A-D-E singularity
ADE classification
In mathematics, the ADE classification is the complete list of simply laced Dynkin diagrams or other mathematical objects satisfying analogous axioms; "simply laced" means that there are no multiple edges, which corresponds to all simple roots in the root system forming angles of \pi/2 = 90^\circ ...
. They are the canonical singularities in dimension 2. They were studied by and Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
.
The du Val singularities also appear as quotients of C2 by a finite subgroup of SL2(C); equivalently, a finite subgroup of SU(2), which are known as binary polyhedral groups. The rings of invariant polynomial
Invariant polynomial
In mathematics, an invariant polynomial is a polynomial P that is invariant under a group \Gamma acting on a vector space V. Therefore P is a \Gamma-invariant polynomial ifP = Pfor all \gamma \in \Gamma and x \in V....
s of these finite group actions were computed by Klein, and are essentially the coordinate rings of the singularities; this is a classic result in invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
.
Classification
The possible du Val singularities are (up to analytic isomorphism):- An:

- Dn:
 (n≥4)
(n≥4) - E6:

- E7:
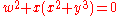
- E8:


