Dynamic errors of numerical methods of ODE discretization
Encyclopedia
The dynamical characteristic of the numerical method of ordinary differential equations (ODE) discretization – is the natural logarithm of its function of stability
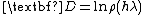. Dynamic characteristic is considered in three forms:
The dynamic characteristic represents the transformation operator of eigenvalues of a Jacobian matrix of the initial differential mathematical model (MM) in eigenvalues of a Jacobian matrix of mathematical model (also differential) whose exact solution passes through the discrete sequence of points of the initial MM solution received by given numerical method.
Stiff equation
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
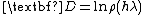. Dynamic characteristic is considered in three forms:-
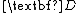– Complex dynamic characteristic; -
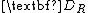– Real dynamic characteristics; -
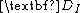– Imaginary dynamic characteristics.
The dynamic characteristic represents the transformation operator of eigenvalues of a Jacobian matrix of the initial differential mathematical model (MM) in eigenvalues of a Jacobian matrix of mathematical model (also differential) whose exact solution passes through the discrete sequence of points of the initial MM solution received by given numerical method.
See also
- Euler's method
- Runge–Kutta methodsRunge–Kutta methodsIn numerical analysis, the Runge–Kutta methods are an important family of implicit and explicit iterative methods for the approximation of solutions of ordinary differential equations. These techniques were developed around 1900 by the German mathematicians C. Runge and M.W. Kutta.See the article...
- Runge–Kutta method (SDE)Runge–Kutta method (SDE)In mathematics, the Runge–Kutta method is a technique for the approximate numerical solution of a stochastic differential equation. It is a generalization of the Runge–Kutta method for ordinary differential equations to stochastic differential equations....
- List of Runge–Kutta methods