Dynamic treatment regimes
Encyclopedia
In medical research, a dynamic treatment regime (DTR) or adaptive treatment strategy is a set of rules for choosing effective treatments for individual patients. The treatment choices made for a particular patient are based on that individual's characteristics and history, with the goal of optimizing his or her long-term clinical outcome. A dynamic treatment regime is analogous to a policy in the field of reinforcement learning
, and analogous to a controller
in control theory
. While most work on dynamic treatment regimes has been done in the context of medicine, the same ideas apply to time-varying policies in other fields, such as education, marketing, and economics.
model for the treatment of all medical problems, including chronic illness . More recently, the medical field has begun to look at long term care plans to treat patients with a chronic illness. This shift in ideology, coupled with increased demand for evidence based medicine and individualized care, has led to the application of sequential decision making research to medical problems and the formulation of dynamic treatment regimes.
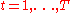, define 
to be the treatment ("action") chosen at time point 
, and define 
to be all clinical observations made at time 
, immediately prior to treatment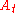 
. A dynamic treatment regime, 
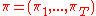consists of a set of rules, one for each for each time point 
, for choosing treatment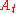 
based clinical observations 
. Thus 
, is a function of the past and current observations, 
and past treatments 
, which returns a choice of the current treatment,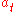 
.
Also observed at each time point is a measure of success called a reward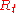
. The goal of a dynamic treatment regime is to make decisions that result in the largest possible expected sum of rewards, . A dynamic treatment regime, 
is optimal if it satisfies
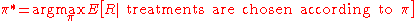
where
is an expectation over possible observations and rewards. The quantity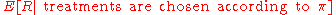 
is often referred to as the value of 
.
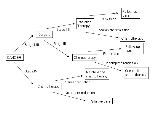
In the example above, the possible first treatments for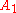
are "Low-Dose B-mod" and "Low-Dose Medication". The possible second treatments for 
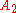are "Increase B-mod Dose", "Continue Treatment", and "Augment w/B-mod". The observations 
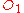and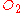 
are the labels on the arrows: The possible 
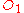are "Less Severe" and "More Severe", and the possible 
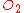are "Non-Response" and "Response". The rewards 
are not shown; one reasonable possibility for reward would be to set 
and set 
to a measure of classroom performance after a fixed amount of time.
For example a treatment may be desirable as a first treatment even if it does not achieve a high immediate reward. For example, when treating some kinds of cancer, a particular medication may not result in the best immediate reward (best acute effect) among initial treatments. However, this medication may impose sufficiently low side effects so that some non-responders are able to become responders with further treatment. Similarly a treatment that is less effective acutely may lead to better overall rewards, if it encourages/enables non-responders to adhere more closely to subsequent treatments.
, where clinical decision making is informed by data on how patients respond to different treatments. The data used to find optimal dynamic treatment regimes consist of the sequence of observations and treatments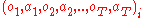
for multiple patients 
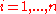along with those patients' rewards 
. A central difficulty is that intermediate outcomes both depend on previous treatments and determine subsequent treatment. However, if treatment assignment is independent of potential outcomes conditional on past observations—i.e., treatment is sequentially unconfounded—a number of algorithms exist to estimate the causal effect of time-varying treatments or dynamic treatment regimes.
While this type of data can be obtained through careful observation, it is often preferable to collect data through experimentation if possible. The use of experimental data, where treatments have been randomly assigned, is preferred because it helps eliminate bias
caused by unobserved confounding variables that influence both the choice of the treatment and the clinical outcome. This is especially important when dealing with sequential treatments, since these biases can compound over time. Given an experimental data set, an optimal dynamic treatment regime can be estimated from the data using a number of different algorithms. Inference can also be done to determine whether the estimated optimal dynamic treatment regime results in significant improvements in expected reward over an alternative dynamic treatment regime.
SMART trials attempt to mimic the decision-making that occurs in clinical practice, but still retain the advantages of experimentation over observation. They can be more involved than single-stage randomized trials; however, they produce the data trajectories necessary for estimating optimal policies that take delayed effects into account. Several suggestions have been made to attempt to reduce complexity and resources needed. One can combine data over same treatment sequences within different treatment regimes. One may also wish to split up a large trial into screening, refining, and confirmatory trials . One can also use fractional factorial designs
rather than a full factorial design , or target primary analyses to simple regime comparisons .
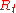. To construct a useful reward, the goals of the treatment need to be well defined and quantifiable. The goals of the treatment can include multiple aspects of a patient's health and welfare, such as degree of symptoms, severity of side effects, time until treatment response, quality of life and cost. However, quantifying the various aspects of a successful treatment with a single function can be difficult, and work on providing useful decision making support that analyzes multiple outcomes is ongoing . Ideally, the outcome variable should reflect how successful the treatment regime was in achieving the overall goals for each patient.
methods . The most popular of these methods used to estimate dynamic treatment regimes is called q-learning
. In q-learning models are fit sequentially to estimate the value of the treatment regime used to collect the data and then the models are optimized with respect to the treatmens to find the best dynamic treatment regime. Many variations of this algorithm exist including modeling only portions of the Value of the treatment regime . Using model-based Bayesian methods, the optimal treatment regime can also be calculated directly from posterior predictive inferences on the effect of dynamic policies .
Reinforcement learning
Inspired by behaviorist psychology, reinforcement learning is an area of machine learning in computer science, concerned with how an agent ought to take actions in an environment so as to maximize some notion of cumulative reward...
, and analogous to a controller
Controller (control theory)
In control theory, a controller is a device which monitors and affects the operational conditions of a given dynamical system. The operational conditions are typically referred to as output variables of the system which can be affected by adjusting certain input variables...
in control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
. While most work on dynamic treatment regimes has been done in the context of medicine, the same ideas apply to time-varying policies in other fields, such as education, marketing, and economics.
History
Historically, medical research and the practice of medicine tended to rely on an acute careAcute care
Acute care is a branch of secondary health care where a patient receives active but short-term treatment for a severe injury or episode of illness, an urgent medical condition, or during recovery from surgery...
model for the treatment of all medical problems, including chronic illness . More recently, the medical field has begun to look at long term care plans to treat patients with a chronic illness. This shift in ideology, coupled with increased demand for evidence based medicine and individualized care, has led to the application of sequential decision making research to medical problems and the formulation of dynamic treatment regimes.
Example
The figure below illustrates a hypothetical dynamic treatment regime for Attention Deficit Hyperactivity Disorder (ADHD). There are two decision points in this DTR. The initial treatment decision depends on the patient's baseline disease severity. The second treatment decision is a "responder/non-responder" decision: At some time after receiving the first treatment, the patient is assessed for response, i.e. whether or not the initial treatment has been effective. If so, that treatment is continued. If not, the patient receives a different treatment. In this example, for those who did not respond to initial medication, the second "treatment" is a package of treatments—it is the initial treatment plus behavior modification therapy. "Treatments" can be defined as whatever interventions are appropriate, whether they take the form of medications or other therapies.Optimal Dynamic Treatment Regimes
The decisions of a dynamic treatment regime are made in the service of producing favorable clinical outcomes in patients who follow it. To make this more precise, the following mathematical framework is used:Mathematical Formulation
For a series of decision time points,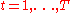, define to be the treatment ("action") chosen at time point , and define to be all clinical observations made at time , immediately prior to treatment 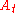. A dynamic treatment regime, 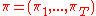consists of a set of rules, one for each for each time point , for choosing treatment 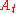based clinical observations . Thus , is a function of the past and current observations, and past treatments , which returns a choice of the current treatment, 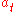.Also observed at each time point is a measure of success called a reward
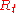. The goal of a dynamic treatment regime is to make decisions that result in the largest possible expected sum of rewards, . A dynamic treatment regime, is optimal if it satisfies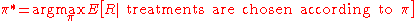where
is an expectation over possible observations and rewards. The quantity 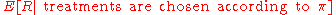is often referred to as the value of .In the example above, the possible first treatments for
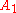are "Low-Dose B-mod" and "Low-Dose Medication". The possible second treatments for 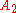are "Increase B-mod Dose", "Continue Treatment", and "Augment w/B-mod". The observations 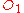and 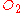are the labels on the arrows: The possible 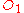are "Less Severe" and "More Severe", and the possible 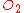are "Non-Response" and "Response". The rewards are not shown; one reasonable possibility for reward would be to set and set to a measure of classroom performance after a fixed amount of time.Delayed Effects
To find an optimal dynamic treatment regime, it might seem reasonable to find the optimal treatment that maximizes the immediate reward at each time point and then patch these treatment steps together to create a dynamic treatment regime. However, this approach is shortsighted and can result in an inferior dynamic treatment regime, because it ignores the potential for the current treatment action to influence the reward obtained at more distant time points.For example a treatment may be desirable as a first treatment even if it does not achieve a high immediate reward. For example, when treating some kinds of cancer, a particular medication may not result in the best immediate reward (best acute effect) among initial treatments. However, this medication may impose sufficiently low side effects so that some non-responders are able to become responders with further treatment. Similarly a treatment that is less effective acutely may lead to better overall rewards, if it encourages/enables non-responders to adhere more closely to subsequent treatments.
Estimating Optimal Dynamic Treatment Regimes
Dynamic treatment regimes can be developed in the framework of evidence-based medicineEvidence-based medicine
Evidence-based medicine or evidence-based practice aims to apply the best available evidence gained from the scientific method to clinical decision making. It seeks to assess the strength of evidence of the risks and benefits of treatments and diagnostic tests...
, where clinical decision making is informed by data on how patients respond to different treatments. The data used to find optimal dynamic treatment regimes consist of the sequence of observations and treatments
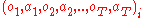for multiple patients 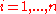along with those patients' rewards . A central difficulty is that intermediate outcomes both depend on previous treatments and determine subsequent treatment. However, if treatment assignment is independent of potential outcomes conditional on past observations—i.e., treatment is sequentially unconfounded—a number of algorithms exist to estimate the causal effect of time-varying treatments or dynamic treatment regimes.While this type of data can be obtained through careful observation, it is often preferable to collect data through experimentation if possible. The use of experimental data, where treatments have been randomly assigned, is preferred because it helps eliminate bias
Bias
Bias is an inclination to present or hold a partial perspective at the expense of alternatives. Bias can come in many forms.-In judgement and decision making:...
caused by unobserved confounding variables that influence both the choice of the treatment and the clinical outcome. This is especially important when dealing with sequential treatments, since these biases can compound over time. Given an experimental data set, an optimal dynamic treatment regime can be estimated from the data using a number of different algorithms. Inference can also be done to determine whether the estimated optimal dynamic treatment regime results in significant improvements in expected reward over an alternative dynamic treatment regime.
Experimental design
Experimental designs of clinical trials that generate data for estimating optimal dynamic treatment regimes involve an initial randomization of patients to treatments, followed by re-randomizations at each subsequent time point to another treatment. The re-randomizations at each subsequent time point my depend on information collected after previous treatments, but prior to assigning the new treatment, such as how successful the previous treatment was. These types of trials were introduced and developed in , and and are often referred to as SMART trials (Sequential Multiple Assignment Randomized Trial). Some examples of SMART trials are the CATIE trial for treatment of Alzheimer's and the STAR*D trial for treatment of major depressive disorder .SMART trials attempt to mimic the decision-making that occurs in clinical practice, but still retain the advantages of experimentation over observation. They can be more involved than single-stage randomized trials; however, they produce the data trajectories necessary for estimating optimal policies that take delayed effects into account. Several suggestions have been made to attempt to reduce complexity and resources needed. One can combine data over same treatment sequences within different treatment regimes. One may also wish to split up a large trial into screening, refining, and confirmatory trials . One can also use fractional factorial designs
Fractional factorial designs
In statistics, fractional factorial designs are experimental designs consisting of a carefully chosen subset of the experimental runs of a full factorial design...
rather than a full factorial design , or target primary analyses to simple regime comparisons .
Reward construction
A critical part of finding the best dynamic treatment regime is the construction of a meaningful and comprehensive reward variable,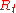. To construct a useful reward, the goals of the treatment need to be well defined and quantifiable. The goals of the treatment can include multiple aspects of a patient's health and welfare, such as degree of symptoms, severity of side effects, time until treatment response, quality of life and cost. However, quantifying the various aspects of a successful treatment with a single function can be difficult, and work on providing useful decision making support that analyzes multiple outcomes is ongoing . Ideally, the outcome variable should reflect how successful the treatment regime was in achieving the overall goals for each patient.Variable selection and feature construction
Analysis is often improved by the collection of any variables that might be related to the illness or the treatment. This is especially important when data is collected by observation, to avoid bias in the analysis due to unmeasured confounders. Subsequently more observation variables are collected than are actually needed to estimate optimal dynamic treatment regimes. Thus variable selection is often required as a preprocessing step on the data before algorithms used to find the best dynamic treatment regime are employed.Algorithms and Inference
Several algorithms exist for estimating optimal dynamic treatment regimes from data. Many of these algorithms were developed in the field of computer science to help robots and computers make optimal decisions in an interactive environment. These types of algorithms are often referred to as reinforcement learningReinforcement learning
Inspired by behaviorist psychology, reinforcement learning is an area of machine learning in computer science, concerned with how an agent ought to take actions in an environment so as to maximize some notion of cumulative reward...
methods . The most popular of these methods used to estimate dynamic treatment regimes is called q-learning
Q-learning
Q-learning is a reinforcement learning technique that works by learning an action-value function that gives the expected utility of taking a given action in a given state and following a fixed policy thereafter. One of the strengths of Q-learning is that it is able to compare the expected utility...
. In q-learning models are fit sequentially to estimate the value of the treatment regime used to collect the data and then the models are optimized with respect to the treatmens to find the best dynamic treatment regime. Many variations of this algorithm exist including modeling only portions of the Value of the treatment regime . Using model-based Bayesian methods, the optimal treatment regime can also be calculated directly from posterior predictive inferences on the effect of dynamic policies .
See also
- Personalized medicinePersonalized medicinePersonalized medicine is a medical model emphasizing in general the customization of healthcare, with all decisions and practices being tailored to individual patients in whatever ways possible...
- Reinforcement learningReinforcement learningInspired by behaviorist psychology, reinforcement learning is an area of machine learning in computer science, concerned with how an agent ought to take actions in an environment so as to maximize some notion of cumulative reward...
- Q learning
- Optimal controlOptimal controlOptimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
- Multi-armed banditMulti-armed banditIn statistics, particularly in the design of sequential experiments, a multi-armed bandit takes its name from a traditional slot machine . Multiple levers are considered in the motivating applications in statistics. When pulled, each lever provides a reward drawn from a distribution associated...