Eccentric anomaly
Encyclopedia
In celestial mechanics
, the eccentric anomaly is an angular
parameter
that defines the position of a body that is moving along an elliptic
Kepler orbit
.
For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure. It is determined by drawing a vertical line from the major axis of the ellipse through the point P and locating its intercept P′ with the auxiliary circle, a circle of radius a (the semi-major axis of the ellipse) that enscribes the entire ellipse. This intersection P′ is called the corresponding point to P. The radius of the auxiliary circle passing through the corresponding point makes an angle E with the major axis.
The eccentric anomaly is one of three angular parameters ("anomalies") that define a position along an orbit; the other two being the true anomaly
and the mean anomaly
.
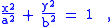
where a and b are the semi-major and semi-minor axes determining the length (2a) and width (2b) of the ellipse.
The eccentric anomaly E in terms of these coordinates is given by:
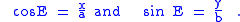
The above equations can be established by drawing the auxiliary circle of radius a enclosing the elliptical path and the minor auxiliary circle of radius b inscribed within the path. The first equation is established by the definition of E. By extending a vertical line through point P to the auxiliary circle, a right triangle is formed with base that is the x-coordinate of P, and hypotenuse a, establishing the first equation. The second equation is established using the minor auxiliary circle. A horizontal line through P intersects this minor auxiliary circle of radius b, establishing another right triangle with altitude y and hypotenuse b. Labeling the adjacent angle E′:
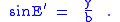
It is next established that E′ = E. From the equation for the ellipse and the Pythagorean trigonometric identity
:
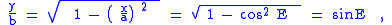
establishing E′ = E.
e is defined as:
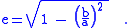
From Pythagoras' theorem applied to the triangle with r as hypotenuse: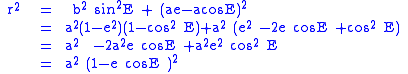
Thus, the radius (distance from the focus to point P) is related to the eccentric anomaly by the formula
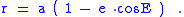
With this result the eccentric anomaly can be determined from the true anomaly as shown next.
is the angle labeled θ in the figure, located at the focus of the ellipse. The true anomaly and the eccentric anomaly can be related as follows.
Using the formula for r above, the sine and cosine of E are found in terms of θ: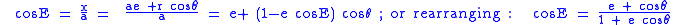
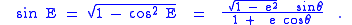
Hence,
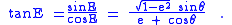
Angle E is therefore the adjacent angle of a right triangle with hypotenuse 1 + e cosθ, adjacent side e + cosθ, and opposite side √(1-e2) sinθ.
Also,
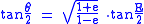
Substituting cosE as found above into the expression for r, the radial distance from the focal point to the point P, can be found in terms of the true anomaly as well:
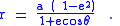
is related to the mean anomaly
by the formula:
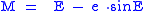
This equation does not have a closed-form solution for
given 
. It is usually solved by numerical methods, e.g. Newton-Raphson method
.
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, the eccentric anomaly is an angular
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
that defines the position of a body that is moving along an elliptic
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
Kepler orbit
Kepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
.
For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure. It is determined by drawing a vertical line from the major axis of the ellipse through the point P and locating its intercept P′ with the auxiliary circle, a circle of radius a (the semi-major axis of the ellipse) that enscribes the entire ellipse. This intersection P′ is called the corresponding point to P. The radius of the auxiliary circle passing through the corresponding point makes an angle E with the major axis.
The eccentric anomaly is one of three angular parameters ("anomalies") that define a position along an orbit; the other two being the true anomaly
True anomaly
In celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
and the mean anomaly
Mean anomaly
In celestial mechanics, the mean anomaly is a parameter relating position and time for a body moving in a Kepler orbit. It is based on the fact that equal areas are swept at the focus in equal intervals of time....
.
Coordinates
If the center of coordinates is taken as the center of the ellipse, the coordinates of a point P(x, y) on the ellipse satisfy the equation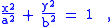where a and b are the semi-major and semi-minor axes determining the length (2a) and width (2b) of the ellipse.
The eccentric anomaly E in terms of these coordinates is given by:
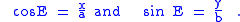
The above equations can be established by drawing the auxiliary circle of radius a enclosing the elliptical path and the minor auxiliary circle of radius b inscribed within the path. The first equation is established by the definition of E. By extending a vertical line through point P to the auxiliary circle, a right triangle is formed with base that is the x-coordinate of P, and hypotenuse a, establishing the first equation. The second equation is established using the minor auxiliary circle. A horizontal line through P intersects this minor auxiliary circle of radius b, establishing another right triangle with altitude y and hypotenuse b. Labeling the adjacent angle E′:
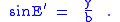
It is next established that E′ = E. From the equation for the ellipse and the Pythagorean trigonometric identity
Pythagorean trigonometric identity
The Pythagorean trigonometric identity is a trigonometric identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one the basic relations between the sine and cosine functions, from which all others may be derived.-Statement of...
:
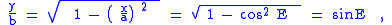
establishing E′ = E.
Radius and eccentric anomaly
The eccentricityEccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
e is defined as:
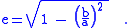
From Pythagoras' theorem applied to the triangle with r as hypotenuse:
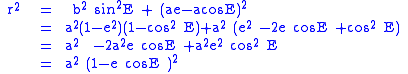
Thus, the radius (distance from the focus to point P) is related to the eccentric anomaly by the formula
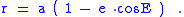
With this result the eccentric anomaly can be determined from the true anomaly as shown next.
From the true anomaly
The true anomalyTrue anomaly
In celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
is the angle labeled θ in the figure, located at the focus of the ellipse. The true anomaly and the eccentric anomaly can be related as follows.
Using the formula for r above, the sine and cosine of E are found in terms of θ:
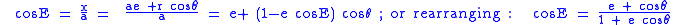
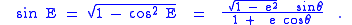
Hence,
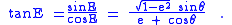
Angle E is therefore the adjacent angle of a right triangle with hypotenuse 1 + e cosθ, adjacent side e + cosθ, and opposite side √(1-e2) sinθ.
Also,
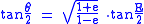
Substituting cosE as found above into the expression for r, the radial distance from the focal point to the point P, can be found in terms of the true anomaly as well:
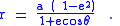
From the mean anomaly
The eccentric anomaly is related to the mean anomalyMean anomaly
In celestial mechanics, the mean anomaly is a parameter relating position and time for a body moving in a Kepler orbit. It is based on the fact that equal areas are swept at the focus in equal intervals of time....
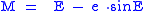
by the formula:This equation does not have a closed-form solution for
given . It is usually solved by numerical methods, e.g. Newton-Raphson methodNewton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
.
Background references
- Murray, C. D. & Dermott, S. F. 1999, Solar System Dynamics, Cambridge University Press, Cambridge.
- Plummer, H.C., 1960, An Introductory treatise on Dynamical Astronomy, Dover Publications, New York. (Reprint of the 1918 Cambridge University Press edition.)