Eddington-Finkelstein coordinates
Encyclopedia
In general relativity
Eddington–Finkelstein coordinates, named for Arthur Stanley Eddington
and David Finkelstein
, are a pair of coordinate system
s for a Schwarzschild geometry which are adapted to radial null geodesics (i.e. the worldlines of photon
s moving directly towards or away from the central mass). One advantage of this coordinate system is that it shows that the apparent singularity at the Schwarzschild radius
is only a coordinate singularity and not a true physical singularity.
Conventions: In this article the metric signature
(− + + +) will be used as will unit
s where c = 1. The gravitational constant
G will be kept explicit and M will denote the characteristic mass of the Schwarzschild geometry.
Recall that in Schwarzschild coordinates
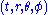, the Schwarzschild metric is given by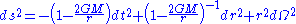
where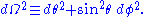
Define the tortoise coordinate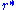
by
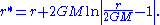
The tortoise coordinate approaches −∞ as r approaches the Schwarzschild radius r = 2GM. It satisfies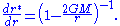
Now define the ingoing and outgoing null coordinates by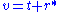
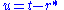
These are so named because the ingoing radial null geodesics are given by v = constant, while the outgoing ones are given by u = constant.
The ingoing Eddington–Finkelstein coordinates are obtained by replacing t with v. The metric in these coordinates can be written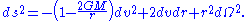
Likewise, the outgoing Eddington–Finkelstein coordinates are obtained by replacing t with u. The metric is then given by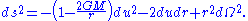
In both these coordinate systems the metric is explicitly non-singular at the Schwarzschild radius (even though one component vanishes at this radius, the determinant of the metric is still non-vanishing).
In ingoing coordinates the equations for the radial null curves are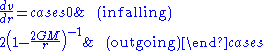
while in outgoing coordinates the equations are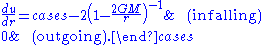
Note that dv/dr and du/dr approach 0 and ±2 at large r, not ±1 as one might expect. In Eddington-Finkelstein diagrams, surfaces of constant u or v are usually drawn as cones rather than planes (see for instance Box 31.2 of MTW
). Some sources instead take
, corresponding to planar surfaces in such diagrams. In terms of this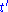 
the metric becomes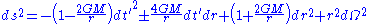
which is Minkowskian at large r.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
Eddington–Finkelstein coordinates, named for Arthur Stanley Eddington
Arthur Stanley Eddington
Sir Arthur Stanley Eddington, OM, FRS was a British astrophysicist of the early 20th century. He was also a philosopher of science and a popularizer of science...
and David Finkelstein
David Finkelstein
David Ritz Finkelstein is currently an emeritus professor of physics at the Georgia Institute of Technology. Finkelstein obtained his Ph.D. in physics at the Massachusetts Institute of Technology in 1953. From 1964 to 1976, he was professor of physics at Yeshiva University.In 1958 Charles W...
, are a pair of coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
s for a Schwarzschild geometry which are adapted to radial null geodesics (i.e. the worldlines of photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s moving directly towards or away from the central mass). One advantage of this coordinate system is that it shows that the apparent singularity at the Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
is only a coordinate singularity and not a true physical singularity.
Conventions: In this article the metric signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(− + + +) will be used as will unit
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
s where c = 1. The gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
G will be kept explicit and M will denote the characteristic mass of the Schwarzschild geometry.
Recall that in Schwarzschild coordinates
Schwarzschild coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
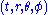, the Schwarzschild metric is given by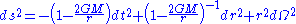where
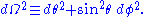
Define the tortoise coordinate
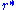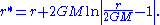
byThe tortoise coordinate approaches −∞ as r approaches the Schwarzschild radius r = 2GM. It satisfies
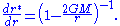
Now define the ingoing and outgoing null coordinates by
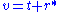
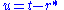
These are so named because the ingoing radial null geodesics are given by v = constant, while the outgoing ones are given by u = constant.
The ingoing Eddington–Finkelstein coordinates are obtained by replacing t with v. The metric in these coordinates can be written
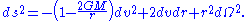
Likewise, the outgoing Eddington–Finkelstein coordinates are obtained by replacing t with u. The metric is then given by
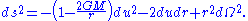
In both these coordinate systems the metric is explicitly non-singular at the Schwarzschild radius (even though one component vanishes at this radius, the determinant of the metric is still non-vanishing).
In ingoing coordinates the equations for the radial null curves are
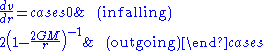
while in outgoing coordinates the equations are
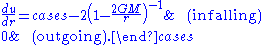
Note that dv/dr and du/dr approach 0 and ±2 at large r, not ±1 as one might expect. In Eddington-Finkelstein diagrams, surfaces of constant u or v are usually drawn as cones rather than planes (see for instance Box 31.2 of MTW
Gravitation (book)
In physics, Gravitation is a very important reference book on Einstein's theory of gravity by Charles W. Misner, Kip S. Thorne, and John Archibald Wheeler. Often considered the "Bible" of General Relativity by researchers for its prominence. It is frequently called MTW after its authors' initials....
). Some sources instead take
, corresponding to planar surfaces in such diagrams. In terms of this 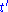the metric becomes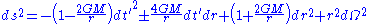which is Minkowskian at large r.
See also
- Schwarzschild coordinatesSchwarzschild coordinatesIn the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
- Kruskal-Szekeres coordinatesKruskal-Szekeres coordinatesIn general relativity Kruskal–Szekeres coordinates, named for Martin Kruskal and George Szekeres, are a coordinate system for the Schwarzschild geometry for a black hole...
- Lemaitre coordinates