
Ehrenfeucht–Mycielski sequence
Encyclopedia
The Ehrenfeucht–Mycielski sequence is a recursively defined sequence of binary digits with pseudorandom properties, defined by .
For example, the first few steps of this construction process are:
The first few digits of the sequence are:
, the sequence can be generated much more efficiently, in constant time per generated digit.
. Experimentally, however, each subsequence appears much earlier in this sequence than this upper bound would suggest: the position by which all length-i sequences occur, up to the limit of experimental testing, is close to the minimum possible value it could be, 2i + i, the position by which a de Bruijn sequence
contains all length-i substrings .
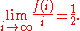
More strongly, I. J. Good
suggests that the convergence rate of this limit should be significantly faster than that of a random binary sequence
, for which (by the law of the iterated logarithm
)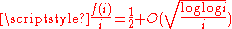 .
.
The Ehrenfeucht–Mycielski balance conjecture suggests that the binary number 0.01001101... (the number having the Ehrenfeucht–Mycielski sequence as its sequence of binary digits after the binary point) may be a normal number
in base 2.
As of 2009 this conjecture remains unproven ; however, it is known that every limit point of the sequence of values f(i)/i lies within the interval [1/4,3/4] .
Definition
The sequence starts with the three bits 010; each successive digit is formed by finding the longest suffix of the sequence that also appears earlier within the sequence, and complementing the bit following the most recent earlier appearance of that suffix.For example, the first few steps of this construction process are:
- 010: initial state
- 0100: the suffix "0" of "010" occurs earlier followed by a 1, so add 0
- 01001: the suffix "0" of "0100" occurs twice earlier with the latest occurrence followed by a 0, so add 1
- 010011: the suffix "01" of "01001" occurs earlier followed by a 0, so add 1
- 0100110: the suffix "1" of "010011" occurs twice earlier with the latest occurrence followed by a 1, so add 0
The first few digits of the sequence are:
- 010011010111000100001111... .
Algorithms
A naive algorithm that generates each bit in the sequence by comparing each suffix with the entire previous sequence could take as much as O(n3) time to generate the first n bits of the sequence; however, as show using a data structure related to a suffix treeSuffix tree
In computer science, a suffix tree is a data structure that presents the suffixes of a given string in a way that allows for a particularly fast implementation of many important string operations.The suffix tree for a string S is a tree whose edges are labeled with strings, such that each suffix...
, the sequence can be generated much more efficiently, in constant time per generated digit.
Universality
Every finite subsequence of bits occurs contiguously, infinitely often within the sequence . More explicitly, the position by which every subsequence of length i can be guaranteed to have occurred at least j times is at most A(4i,j), where A is the Ackermann functionAckermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
. Experimentally, however, each subsequence appears much earlier in this sequence than this upper bound would suggest: the position by which all length-i sequences occur, up to the limit of experimental testing, is close to the minimum possible value it could be, 2i + i, the position by which a de Bruijn sequence
De Bruijn sequence
In combinatorial mathematics, a k-ary De Bruijn sequence B of order n, named after the Dutch mathematician Nicolaas Govert de Bruijn, is a cyclic sequence of a given alphabet A with size k for which every possible subsequence of length n in A appears as a sequence of consecutive characters exactly...
contains all length-i substrings .
Normality
conjecture that the numbers of 0 and 1 bits each converge to a limiting density of 1/2. That is, if f(i) denotes the number of 0 bits in the first i positions of the Ehrenfeucht–Mycielski sequence, then it should be the case that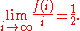
More strongly, I. J. Good
I. J. Good
Irving John Good was a British mathematician who worked as a cryptologist at Bletchley Park with Alan Turing. After World War II, Good continued to work with Turing on the design of computers and Bayesian statistics at the University of Manchester...
suggests that the convergence rate of this limit should be significantly faster than that of a random binary sequence
Random sequence
The concept of a random sequence is essential in probability theory and statistics. The concept generally relies on the notion of a sequence of random variables and many statistical discussions begin with the words "let X1,...,Xn be independent random variables...". Yet as D. H. Lehmer stated in...
, for which (by the law of the iterated logarithm
Law of the iterated logarithm
In probability theory, the law of the iterated logarithm describes the magnitude of the fluctuations of a random walk. The original statement of the law of the iterated logarithm is due to A. Y. Khinchin . Another statement was given by A.N...
)
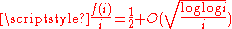 .
.The Ehrenfeucht–Mycielski balance conjecture suggests that the binary number 0.01001101... (the number having the Ehrenfeucht–Mycielski sequence as its sequence of binary digits after the binary point) may be a normal number
Normal number
In mathematics, a normal number is a real number whose infinite sequence of digits in every base b is distributed uniformly in the sense that each of the b digit values has the same natural density 1/b, also all possible b2 pairs of digits are equally likely with density b−2,...
in base 2.
As of 2009 this conjecture remains unproven ; however, it is known that every limit point of the sequence of values f(i)/i lies within the interval [1/4,3/4] .
External links
- One million terms of the sequence calculated by Terry McConnell at Syracuse University.

