
Eigenvector slew
Encyclopedia
In aerospace engineering
, especially those areas dealing with spacecraft
, the eigenvector slew is a method to calculate a steering correction (called a slew
) by rotating the spacecraft around one fixed axis. This corresponds in general to the fastest and most efficient way to reach the desired target orientation as there is only one acceleration phase and one braking phase for the angular rate. If this fixed axis is not a principal axis a time varying torque must be applied to force the spacecraft to rotate as desired, though. Also the gyroscopic
effect of momentum wheels must be compensated for.
That such a rotation exists corresponds precisely to a main result of the mathematical theory of rotation operators
, the (only real) eigenvector of the rotation operator corresponding to the desired re-orientation is this axis.
Given the current orientation of the craft, and the desired orientation of the craft in cartesian coordinates, the required axis of rotation and corresponding rotation angle to achieve the new orientation is determined by computing the eigenvector of the rotation operator
.

be a body fixed reference system for a 3 axis stabilized spacecraft
. The initial attitude
is given by



One wants to find an axis relative the spacecraft body

and a rotation angle such that after the rotation with the angle
such that after the rotation with the angle  one has that
one has that



where
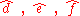
are the new target directions.
In vector form this means that
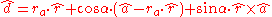
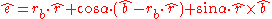

this means that one wants to find an eigenvector with the eigenvalue = 1 for the linear mapping defined by



which relative to the

coordinate system has the matrix
Because this is the matrix of the rotation operator
relative the base vector system the eigenvalue can be determined with the algorithm described in "Rotation operator (vector space)
the eigenvalue can be determined with the algorithm described in "Rotation operator (vector space)
".
With the notations used here this is:

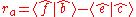
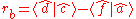
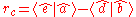

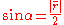
The rotation angle is
is
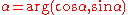
where " " is the polar argument of the vector
" is the polar argument of the vector  corresponding to the function function ATAN2(y,x)
corresponding to the function function ATAN2(y,x)
(or in double precision
DATAN2(y,x)) available in for example the programming language FORTRAN
.
The resulting will be in the interval
will be in the interval  .
.
If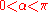 then
then  and the uniquely defined rotation (unit) vector is:
and the uniquely defined rotation (unit) vector is:
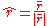
Note that
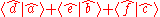
is the trace
of the matrix defined by the orthogonal linear mapping and that the components of the "eigenvector" are fixed and constant during the rotation, i.e.
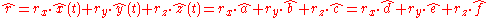
where are moving with time
are moving with time  during the slew.
during the slew.
Aerospace engineering
Aerospace engineering is the primary branch of engineering concerned with the design, construction and science of aircraft and spacecraft. It is divided into two major and overlapping branches: aeronautical engineering and astronautical engineering...
, especially those areas dealing with spacecraft
Spacecraft
A spacecraft or spaceship is a craft or machine designed for spaceflight. Spacecraft are used for a variety of purposes, including communications, earth observation, meteorology, navigation, planetary exploration and transportation of humans and cargo....
, the eigenvector slew is a method to calculate a steering correction (called a slew
Slew (spacecraft)
A spacecraft is either spin stabilized or 3 axis stabilized .For a spin stabilized spacecraft a slew means a change of the direction of the spin axis relative to space. This can be done by applying a torque to the spacecraft, in general by operating a thruster in pulsed mode synchronous to the spin...
) by rotating the spacecraft around one fixed axis. This corresponds in general to the fastest and most efficient way to reach the desired target orientation as there is only one acceleration phase and one braking phase for the angular rate. If this fixed axis is not a principal axis a time varying torque must be applied to force the spacecraft to rotate as desired, though. Also the gyroscopic
Gyroscope
A gyroscope is a device for measuring or maintaining orientation, based on the principles of angular momentum. In essence, a mechanical gyroscope is a spinning wheel or disk whose axle is free to take any orientation...
effect of momentum wheels must be compensated for.
That such a rotation exists corresponds precisely to a main result of the mathematical theory of rotation operators
Rotation operator (vector space)
This article derives the main properties of rotations in 3-dimensional space.The three Euler rotations are one way to bring a rigid object to any desired orientation by sequentially making rotations about axis' fixed relative to the object. However, this can also be achieved with one single...
, the (only real) eigenvector of the rotation operator corresponding to the desired re-orientation is this axis.
Given the current orientation of the craft, and the desired orientation of the craft in cartesian coordinates, the required axis of rotation and corresponding rotation angle to achieve the new orientation is determined by computing the eigenvector of the rotation operator
Rotation operator (vector space)
This article derives the main properties of rotations in 3-dimensional space.The three Euler rotations are one way to bring a rigid object to any desired orientation by sequentially making rotations about axis' fixed relative to the object. However, this can also be achieved with one single...
.
Problem
Let
be a body fixed reference system for a 3 axis stabilized spacecraft
3 axis stabilized spacecraft
3 axis stabilization is a design feature of most modern spacecraft whereby the spacecraft utilizes sensor readings to determine how actuators on the spacecraft can be used to keep it in a desired attitude, or orientation in space.-See also:...
. The initial attitude
is given by



One wants to find an axis relative the spacecraft body

and a rotation angle
 such that after the rotation with the angle
such that after the rotation with the angle  one has that
one has that


where
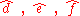
are the new target directions.
In vector form this means that
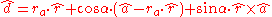
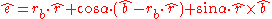

Solution
In terms of linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
this means that one wants to find an eigenvector with the eigenvalue = 1 for the linear mapping defined by



which relative to the

coordinate system has the matrix
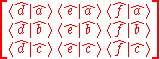
Because this is the matrix of the rotation operator
Rotation operator (vector space)
This article derives the main properties of rotations in 3-dimensional space.The three Euler rotations are one way to bring a rigid object to any desired orientation by sequentially making rotations about axis' fixed relative to the object. However, this can also be achieved with one single...
relative the base vector system
 the eigenvalue can be determined with the algorithm described in "Rotation operator (vector space)
the eigenvalue can be determined with the algorithm described in "Rotation operator (vector space)Rotation operator (vector space)
This article derives the main properties of rotations in 3-dimensional space.The three Euler rotations are one way to bring a rigid object to any desired orientation by sequentially making rotations about axis' fixed relative to the object. However, this can also be achieved with one single...
".
With the notations used here this is:

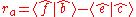
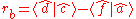
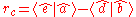

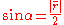
The rotation angle
 is
is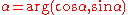
where "
 " is the polar argument of the vector
" is the polar argument of the vector  corresponding to the function function ATAN2(y,x)
corresponding to the function function ATAN2(y,x)Atan2
In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
(or in double precision
Double precision
In computing, double precision is a computer number format that occupies two adjacent storage locations in computer memory. A double-precision number, sometimes simply called a double, may be defined to be an integer, fixed point, or floating point .Modern computers with 32-bit storage locations...
DATAN2(y,x)) available in for example the programming language FORTRAN
Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
.
The resulting
 will be in the interval
will be in the interval  .
.If
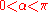 then
then  and the uniquely defined rotation (unit) vector is:
and the uniquely defined rotation (unit) vector is: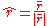
Note that
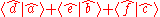
is the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the matrix defined by the orthogonal linear mapping and that the components of the "eigenvector" are fixed and constant during the rotation, i.e.
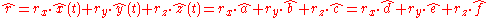
where
 are moving with time
are moving with time  during the slew.
during the slew.See also
- Rotation operator (vector space)Rotation operator (vector space)This article derives the main properties of rotations in 3-dimensional space.The three Euler rotations are one way to bring a rigid object to any desired orientation by sequentially making rotations about axis' fixed relative to the object. However, this can also be achieved with one single...
- Slew (spacecraft)Slew (spacecraft)A spacecraft is either spin stabilized or 3 axis stabilized .For a spin stabilized spacecraft a slew means a change of the direction of the spin axis relative to space. This can be done by applying a torque to the spacecraft, in general by operating a thruster in pulsed mode synchronous to the spin...

