Double precision
Encyclopedia
In computing
, double precision is a computer number format that occupies two adjacent storage locations in computer memory. A double-precision number, sometimes simply called a double, may be defined to be an integer
, fixed point, or floating point
(in which case it is often referred to as FP64).
Modern computers with 32-bit
storage locations use two memory locations to store a 64-bit double-precision number (a single storage location can hold a single-precision number). Double-precision floating-point is an IEEE 754
standard
for encoding binary or decimal floating-point numbers in 64 bits (8 byte
s).
The format is written with the significand
having an implicit integer bit of value 1, unless the written exponent is all zeros. With the 52 bits of the fraction significand appearing in the memory format, the total precision is therefore 53 bits (approximately 16 decimal digits,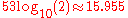
). The bits are laid out as follows:
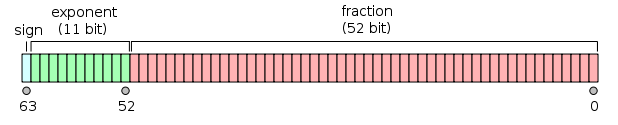
The real value assumed by a given 64-bit double-precision data with a given biased exponent e
and a 52-bit fraction is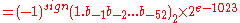
where more precisely we have :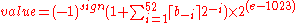
Between 252=4,503,599,627,370,496 and 253=9,007,199,254,740,992 the representable numbers are exactly the integers. For the next range, from 253 to 254, everything is multiplied by 2, so the representable numbers are the even ones, etc. Conversely, for the previous range from 251 to 252, the spacing is 0.5, etc.
The spacing as a fraction of the numbers in the range from 2n to 2n+1 is 2n−52.
The maximum relative rounding error when rounding a number to the nearest representable one (the machine epsilon
) is therefore 2−53.
Thus, as defined by the offset-binary representation, in order to get the true exponent the exponent bias of 1023 has to be subtracted from the written exponent.
The exponents
where F is the fraction mantissa
. All bit patterns are valid encoding.
Here, 0x
is used as the prefix for numeric constants represented in Hexadecimal
according to C notation.
Except for the above exceptions, the entire double-precision number is described by:
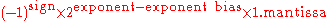
0x 3ff0 0000 0000 0001 ≈ 1.0000000000000002, the next higher number > 1
0x 3ff0 0000 0000 0002 ≈ 1.0000000000000004
0x 4000 0000 0000 0000 = 2
0x c000 0000 0000 0000 = –2
0x 0000 0000 0000 0001 = 2-1022-52 ≈ 4.9406564584124654 x 10−324 (Min subnormal positive double)
0x 000f ffff ffff ffff = 2-1022 - 2-1022-52 ≈ 2.2250738585072009 x 10-308 (Max subnormal positive double)
0x 0010 0000 0000 0000 = 2-1022 ≈ 2.2250738585072014 x 10−308 (Min normal positive double)
0x 7fef ffff ffff ffff = (1 + (1 - 2-52)) x 21023 ≈ 1.7976931348623157 x 10308 (Max Double)
0x 0000 0000 0000 0000 = 0
0x 8000 0000 0000 0000 = –0
0x 7ff0 0000 0000 0000 = Infinity
0x fff0 0000 0000 0000 = −Infinity
0x 3fd5 5555 5555 5555 ≈ 1/3
(1/3 rounds down instead of up like single precision, because of the odd number of bits in the significand.)
In more detail:
Given the hexadecimal representation 0x3fd5 5555 5555 5555,
Sign = 0x0
Exponent = 0x3fd = 1021
Exponent Bias = 1023 (above)
Mantissa = 0x5 5555 5555 5555
Value = 2(Exponent − Exponent Bias) × 1.Mantissa – Note the Mantissa must not be converted to decimal here
= 2–2 × (0x15 5555 5555 5555 × 2–52)
= 2–54 × 0x15 5555 5555 5555
= 0.333333333333333314829616256247390992939472198486328125
≈ 1/3
Computing
Computing is usually defined as the activity of using and improving computer hardware and software. It is the computer-specific part of information technology...
, double precision is a computer number format that occupies two adjacent storage locations in computer memory. A double-precision number, sometimes simply called a double, may be defined to be an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, fixed point, or floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
(in which case it is often referred to as FP64).
Modern computers with 32-bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
storage locations use two memory locations to store a 64-bit double-precision number (a single storage location can hold a single-precision number). Double-precision floating-point is an IEEE 754
IEEE floating-point standard
IEEE 754–1985 was an industry standard for representingfloating-pointnumbers in computers, officially adopted in 1985 and superseded in 2008 byIEEE 754-2008. During its 23 years, it was the most widely used format for...
standard
Standardization
Standardization is the process of developing and implementing technical standards.The goals of standardization can be to help with independence of single suppliers , compatibility, interoperability, safety, repeatability, or quality....
for encoding binary or decimal floating-point numbers in 64 bits (8 byte
Byte
The byte is a unit of digital information in computing and telecommunications that most commonly consists of eight bits. Historically, a byte was the number of bits used to encode a single character of text in a computer and for this reason it is the basic addressable element in many computer...
s).
Double-precision binary floating-point format
Double-precision binary floating-point is a commonly used format on PCs, due to its wider range over single-precision floating point, even if it's at a performance and bandwidth cost. As with single-precision floating-point format, it lacks precision on integer numbers when compared with an integer format of the same size. It is commonly known simply as double. The IEEE 754 standard defines a double as:- Sign bitSign bitIn computer science, the sign bit is a bit in a computer numbering format that indicates the sign of a number. In IEEE format, the sign bit is the leftmost bit...
: 1 bit - Exponent width: 11 bits
- SignificandSignificandThe significand is part of a floating-point number, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.-Examples:...
precisionPrecision (arithmetic)The precision of a value describes the number of digits that are used to express that value. In a scientific setting this would be the total number of digits or, less commonly, the number of fractional digits or decimal places...
: 53 bits (52 explicitly stored)
The format is written with the significand
Significand
The significand is part of a floating-point number, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.-Examples:...
having an implicit integer bit of value 1, unless the written exponent is all zeros. With the 52 bits of the fraction significand appearing in the memory format, the total precision is therefore 53 bits (approximately 16 decimal digits,
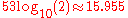). The bits are laid out as follows:The real value assumed by a given 64-bit double-precision data with a given biased exponent e
and a 52-bit fraction is
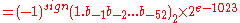
where more precisely we have :
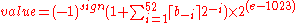
Between 252=4,503,599,627,370,496 and 253=9,007,199,254,740,992 the representable numbers are exactly the integers. For the next range, from 253 to 254, everything is multiplied by 2, so the representable numbers are the even ones, etc. Conversely, for the previous range from 251 to 252, the spacing is 0.5, etc.
The spacing as a fraction of the numbers in the range from 2n to 2n+1 is 2n−52.
The maximum relative rounding error when rounding a number to the nearest representable one (the machine epsilon
Machine epsilon
Machine epsilon gives an upper bound on the relative error due to rounding in floating point arithmetic. This value characterizes computer arithmetic in the field of numerical analysis, and by extension in the subject of computational science...
) is therefore 2−53.
Exponent encoding
The double-precision binary floating-point exponent is encoded using an offset-binary representation, with the zero offset being 1023; also known as exponent bias in the IEEE 754 standard. Examples of such representations would be:- Emin (1) = −1022
- E (50) = −973
- Emax (2046) = 1023
Thus, as defined by the offset-binary representation, in order to get the true exponent the exponent bias of 1023 has to be subtracted from the written exponent.
The exponents
0x000 and 0x7ff have a special meaning:
-
0x000is used to represent zero0 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
(if F=0) and subnormalsDenormal numberIn computer science, denormal numbers or denormalized numbers fill the underflow gap around zero in floating point arithmetic: any non-zero number which is smaller than the smallest normal number is 'sub-normal'.For example, if the smallest positive 'normal' number is 1×β−n In computer...
(if F≠0); and -
0x7ffis used to represent infinityInfinityInfinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
(if F=0) and NaNNaNIn computing, NaN is a value of the numeric data type representing an undefined or unrepresentable value, especially in floating-point calculations...
s (if F≠0),
where F is the fraction mantissa
Significand
The significand is part of a floating-point number, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.-Examples:...
. All bit patterns are valid encoding.
Here, 0x
Hexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
is used as the prefix for numeric constants represented in Hexadecimal
Hexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
according to C notation.
Except for the above exceptions, the entire double-precision number is described by:
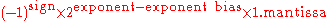
Double-precision examples
0x 3ff0 0000 0000 0000 = 10x 3ff0 0000 0000 0001 ≈ 1.0000000000000002, the next higher number > 1
0x 3ff0 0000 0000 0002 ≈ 1.0000000000000004
0x 4000 0000 0000 0000 = 2
0x c000 0000 0000 0000 = –2
0x 0000 0000 0000 0001 = 2-1022-52 ≈ 4.9406564584124654 x 10−324 (Min subnormal positive double)
0x 000f ffff ffff ffff = 2-1022 - 2-1022-52 ≈ 2.2250738585072009 x 10-308 (Max subnormal positive double)
0x 0010 0000 0000 0000 = 2-1022 ≈ 2.2250738585072014 x 10−308 (Min normal positive double)
0x 7fef ffff ffff ffff = (1 + (1 - 2-52)) x 21023 ≈ 1.7976931348623157 x 10308 (Max Double)
0x 0000 0000 0000 0000 = 0
0x 8000 0000 0000 0000 = –0
0x 7ff0 0000 0000 0000 = Infinity
0x fff0 0000 0000 0000 = −Infinity
0x 3fd5 5555 5555 5555 ≈ 1/3
(1/3 rounds down instead of up like single precision, because of the odd number of bits in the significand.)
In more detail:
Given the hexadecimal representation 0x3fd5 5555 5555 5555,
Sign = 0x0
Exponent = 0x3fd = 1021
Exponent Bias = 1023 (above)
Mantissa = 0x5 5555 5555 5555
Value = 2(Exponent − Exponent Bias) × 1.Mantissa – Note the Mantissa must not be converted to decimal here
= 2–2 × (0x15 5555 5555 5555 × 2–52)
= 2–54 × 0x15 5555 5555 5555
= 0.333333333333333314829616256247390992939472198486328125
≈ 1/3
See also
- IEEE Standard for Floating-Point Arithmetic (IEEE 754)
- Extended precisionExtended precisionThe term extended precision refers to storage formats for floating point numbers not falling into the regular sequence of single, double, and quadruple precision formats...
(80-bit)