Extended precision
Encyclopedia
The term extended precision refers to storage formats for floating point
numbers not falling into the regular sequence of single, double, and quadruple precision formats (usually 32-bit, 64-bit and 128-bit, respectively). In contrast to extended precision, arbitrary-precision arithmetic
refers to implementations of much larger numeric types (with a storage count that usually is not a power of two) using special software (or, rarely, hardware).
The most common extended-precision format is currently the 80-bit format first used in the Intel 8087
math coprocessor
(and later in the Motorola 68881
), which has since become ubiquitous on the x86 architecture
. This 80-bit format uses 64 bits for the significand, 15 bits for the exponent field and one bit for the sign of the significand. The exponent field uses excess-N representation, to be more exact excess-16383, meaning that 16383 has to be subtracted from the written exponent. An exponent field value of 32767 (all fifteen bits 1) is reserved so as to enable the representation of special states such as infinity
and Not a Number
. For historical reasons, this format has no implicit/hidden bit: the explicit bit was used in the Intel 8087
to suppress the normalization of subnormal numbers in certain cases.
The opportunity for extended precision arises because, on the one hand, a number format should fit into a whole number of storage words but must pack in both the mantissa and exponent, and, on the other hand, the hardware performing the arithmetic almost certainly will also be used for integer arithmetic where there is no exponent part. The 64-bit double precision format allows 53 bits for the mantissa and 11 for the exponent, but the hardware also allows 64-bit integer arithmetic. With trivial additional circuitry, it could therefore be generalized to perform floating-point arithmetic on a mantissa of 64 bits, and this additional precision might be useful. But that leaves no room for an exponent, so an additional word of storage is taken (16 bits), for a total of 80 bits or five words. Subtle differences in the behaviour of the arithmetic (in this case) are a side effect.
The 80-bit floating point format was introduced well after the development of most computer languages, which often offer only the common 32- and 64-bit floating point sizes. However, on the x86 architecture
most C
compilers support 80-bit extended precision via the long double
type. Compilers on x86 for other languages often support extended precision as well, sometimes via nonstandard extensions: for example, Turbo Pascal
offers an
compilers have a
and trigonometric function
s, in their standard libraries
.
The common 80-bit format can store 19 whole decimal digits (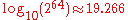
) of precision and has a range from approximately 
to 
.
Older machines used a variety of formats. On an IBM 1130
, "extended precision" referred to a floating-point format that offered a 32-bit significand or mantissa
(corresponding to the 32-bit two's complement
integer
arithmetic of the CPU) for a floating-point number, an extension on the normal 24-bit significand of its standard 32-bit floating-point format. Floating-point arithmetic operations were performed by software, and double precision
was not supported at all. The extended format occupied three 16-bit words, with the extra space simply ignored.
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
numbers not falling into the regular sequence of single, double, and quadruple precision formats (usually 32-bit, 64-bit and 128-bit, respectively). In contrast to extended precision, arbitrary-precision arithmetic
Arbitrary-precision arithmetic
In computer science, arbitrary-precision arithmetic indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most ALU hardware, which typically...
refers to implementations of much larger numeric types (with a storage count that usually is not a power of two) using special software (or, rarely, hardware).
The most common extended-precision format is currently the 80-bit format first used in the Intel 8087
Intel 8087
The Intel 8087, announced in 1980, was the first floating-point coprocessor for the 8086 line of microprocessors. It had 45,000 transistors and was manufactured as a 3 μm depletion load HMOS circuit. The 8087 was built to be paired with the Intel 8088 or 8086 microprocessors...
math coprocessor
Coprocessor
A coprocessor is a computer processor used to supplement the functions of the primary processor . Operations performed by the coprocessor may be floating point arithmetic, graphics, signal processing, string processing, or encryption. By offloading processor-intensive tasks from the main processor,...
(and later in the Motorola 68881
Motorola 68881
The Motorola 68881 and Motorola 68882 were floating-point coprocessor chips that were used in some computer systems in conjunction with the 68020 or 68030 CPUs. The addition of one of these chips added substantial cost to the computer, but added a floating point unit that could rapidly perform...
), which has since become ubiquitous on the x86 architecture
X86 architecture
The term x86 refers to a family of instruction set architectures based on the Intel 8086 CPU. The 8086 was launched in 1978 as a fully 16-bit extension of Intel's 8-bit based 8080 microprocessor and also introduced segmentation to overcome the 16-bit addressing barrier of such designs...
. This 80-bit format uses 64 bits for the significand, 15 bits for the exponent field and one bit for the sign of the significand. The exponent field uses excess-N representation, to be more exact excess-16383, meaning that 16383 has to be subtracted from the written exponent. An exponent field value of 32767 (all fifteen bits 1) is reserved so as to enable the representation of special states such as infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
and Not a Number
NaN
In computing, NaN is a value of the numeric data type representing an undefined or unrepresentable value, especially in floating-point calculations...
. For historical reasons, this format has no implicit/hidden bit: the explicit bit was used in the Intel 8087
Intel 8087
The Intel 8087, announced in 1980, was the first floating-point coprocessor for the 8086 line of microprocessors. It had 45,000 transistors and was manufactured as a 3 μm depletion load HMOS circuit. The 8087 was built to be paired with the Intel 8088 or 8086 microprocessors...
to suppress the normalization of subnormal numbers in certain cases.
The opportunity for extended precision arises because, on the one hand, a number format should fit into a whole number of storage words but must pack in both the mantissa and exponent, and, on the other hand, the hardware performing the arithmetic almost certainly will also be used for integer arithmetic where there is no exponent part. The 64-bit double precision format allows 53 bits for the mantissa and 11 for the exponent, but the hardware also allows 64-bit integer arithmetic. With trivial additional circuitry, it could therefore be generalized to perform floating-point arithmetic on a mantissa of 64 bits, and this additional precision might be useful. But that leaves no room for an exponent, so an additional word of storage is taken (16 bits), for a total of 80 bits or five words. Subtle differences in the behaviour of the arithmetic (in this case) are a side effect.
The 80-bit floating point format was introduced well after the development of most computer languages, which often offer only the common 32- and 64-bit floating point sizes. However, on the x86 architecture
X86 architecture
The term x86 refers to a family of instruction set architectures based on the Intel 8086 CPU. The 8086 was launched in 1978 as a fully 16-bit extension of Intel's 8-bit based 8080 microprocessor and also introduced segmentation to overcome the 16-bit addressing barrier of such designs...
most C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
compilers support 80-bit extended precision via the long double
Long double
In C and related programming languages, long double refers to a floating point data type that is often more precise than double precision. As with C's other floating point types, it may not necessarily map to an IEEE format.-History:...
type. Compilers on x86 for other languages often support extended precision as well, sometimes via nonstandard extensions: for example, Turbo Pascal
Turbo Pascal
Turbo Pascal is a software development system that includes a compiler and an integrated development environment for the Pascal programming language running on CP/M, CP/M-86, and DOS, developed by Borland under Philippe Kahn's leadership...
offers an
extended type, and several FortranFortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
compilers have a
REAL*10 type (analogous to REAL*4 and REAL*8). Such compilers also typically include extended-precision mathematical subroutines, such as square rootSquare root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
and trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s, in their standard libraries
Library (computer science)
In computer science, a library is a collection of resources used to develop software. These may include pre-written code and subroutines, classes, values or type specifications....
.
The common 80-bit format can store 19 whole decimal digits (
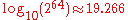) of precision and has a range from approximately to .Older machines used a variety of formats. On an IBM 1130
IBM 1130
The IBM 1130 Computing System was introduced in 1965. It was IBM's least-expensive computer to date, and was aimed at price-sensitive, computing-intensive technical markets like education and engineering. It succeeded the IBM 1620 in that market segment. The IBM 1800 was a process control variant...
, "extended precision" referred to a floating-point format that offered a 32-bit significand or mantissa
Significand
The significand is part of a floating-point number, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.-Examples:...
(corresponding to the 32-bit two's complement
Two's complement
The two's complement of a binary number is defined as the value obtained by subtracting the number from a large power of two...
integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
arithmetic of the CPU) for a floating-point number, an extension on the normal 24-bit significand of its standard 32-bit floating-point format. Floating-point arithmetic operations were performed by software, and double precision
Double precision
In computing, double precision is a computer number format that occupies two adjacent storage locations in computer memory. A double-precision number, sometimes simply called a double, may be defined to be an integer, fixed point, or floating point .Modern computers with 32-bit storage locations...
was not supported at all. The extended format occupied three 16-bit words, with the extra space simply ignored.