Elastic map
Encyclopedia
Elastic maps provide a tool for nonlinear dimensionality reduction
. By their construction, they are system of elastic springs
embedded in the data
space. This system approximates a low-dimensional manifold. The elastic coefficients of this system allow the switch from completely unstructured k-means clustering
(zero elasticity
) to the estimators located closely to linear PCA manifolds (for high bending and low stretching modules). With some intermediate values of the elasticity coefficients, this system effectively approximates non-linear principal manifolds. This approach is based on a mechanical
analogy between principal manifolds, that are passing through "the middle" of data distribution, and elastic membranes and plates. The method was developed by A.N. Gorban, A.Y. Zinovyev and A.A. Pitenko in 1996–1998.
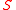 in a finite-dimensional Euclidean space
in a finite-dimensional Euclidean space
. Elastic map is represented by a set of nodes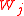 in the same space. For each datapoint
in the same space. For each datapoint  a host node is the closest node
a host node is the closest node 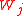 (if there are several closest nodes then one takes the node with the smallest number). The data set
(if there are several closest nodes then one takes the node with the smallest number). The data set 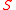 is divided on classes
is divided on classes 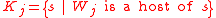 .
.
The approximation energy is distortion
this is the energy of the springs with unite elasticity which connect each data point with its host node.
On the set of nodes an additional structure is defined. Some pairs of nodes,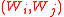 , are connected by elastic edges. Let this set of pairs be
, are connected by elastic edges. Let this set of pairs be  . Some triples of nodes,
. Some triples of nodes, 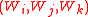 are the bending ribs. Let this set of triples be
are the bending ribs. Let this set of triples be  .
.
where and
and  are the stretching end bending modules.
are the stretching end bending modules.
For example, in the 2D rectangular grid the elastic edges are just vertical and horizontal edges (pairs of closest vertices) and the bending ribs are the vertical or horizontal triples of consecutive (closest) vertices.
The elastic map should be in the mechanical equilibrium: it should minimise the energy .
.
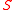 in classes
in classes  minimization of the quadratic functional
minimization of the quadratic functional  is a linear problem with the sparse matrix of coefficients. Therefore, similarly to PCA or k-means, a splitting method is used:
is a linear problem with the sparse matrix of coefficients. Therefore, similarly to PCA or k-means, a splitting method is used:
This expectation-maximization algorithm
guarantees a local minimum of . For improving the approximation various additional methods are proposed. For example, the softening strategy is used. This strategy
. For improving the approximation various additional methods are proposed. For example, the softening strategy is used. This strategy
starts with a rigid grids (small length, small bending and large elasticity modules
 and
and  coefficients) and finishes with soft grids (small
coefficients) and finishes with soft grids (small  and
and  ). The training goes in several epochs, each epoch with its own grid rigidness. Another adaptive strategy is growing net: one starts from small amount of nodes and gradually adds new nodes. Each epoch goes with it own number of nodes.
). The training goes in several epochs, each epoch with its own grid rigidness. Another adaptive strategy is growing net: one starts from small amount of nodes and gradually adds new nodes. Each epoch goes with it own number of nodes.
, for exploratory data analysis and visualisation of multidimensional data, for data visualisation in economics, social and political sciences, as an auxiliary tool for data mapping in geographic informational systems and for visualisation of data of various nature.
Recently, the method is adapted as a support tool in the decision process underlying the selection, optimization, and management of financial portfolios.
Nonlinear dimensionality reduction
High-dimensional data, meaning data that requires more than two or three dimensions to represent, can be difficult to interpret. One approach to simplification is to assume that the data of interest lies on an embedded non-linear manifold within the higher-dimensional space...
. By their construction, they are system of elastic springs
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
embedded in the data
space. This system approximates a low-dimensional manifold. The elastic coefficients of this system allow the switch from completely unstructured k-means clustering
Clustering
Clustering can refer to the following:In demographics:* Clustering , the gathering of various populations based on factors such as ethnicity, economics or religion.In graph theory:...
(zero elasticity
Elasticity
Elasticity may refer to:*Elasticity , continuum mechanics of bodies that deform reversibly under stressNumerous uses are derived from this physical sense of the term, which is inherently mathematical, such as used in Engineering, Chemistry, Construction and variously in Economics:*Elasticity , the...
) to the estimators located closely to linear PCA manifolds (for high bending and low stretching modules). With some intermediate values of the elasticity coefficients, this system effectively approximates non-linear principal manifolds. This approach is based on a mechanical
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
analogy between principal manifolds, that are passing through "the middle" of data distribution, and elastic membranes and plates. The method was developed by A.N. Gorban, A.Y. Zinovyev and A.A. Pitenko in 1996–1998.
Energy of elastic map
Let data set be a set of vectors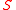 in a finite-dimensional Euclidean space
in a finite-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Elastic map is represented by a set of nodes
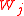 in the same space. For each datapoint
in the same space. For each datapoint  a host node is the closest node
a host node is the closest node 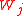 (if there are several closest nodes then one takes the node with the smallest number). The data set
(if there are several closest nodes then one takes the node with the smallest number). The data set 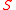 is divided on classes
is divided on classes 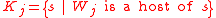 .
.The approximation energy is distortion
this is the energy of the springs with unite elasticity which connect each data point with its host node.
On the set of nodes an additional structure is defined. Some pairs of nodes,
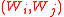 , are connected by elastic edges. Let this set of pairs be
, are connected by elastic edges. Let this set of pairs be  . Some triples of nodes,
. Some triples of nodes, 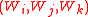 are the bending ribs. Let this set of triples be
are the bending ribs. Let this set of triples be  .
.
- The stretching energy is
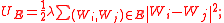
- The bending energy is

where
 and
and  are the stretching end bending modules.
are the stretching end bending modules.For example, in the 2D rectangular grid the elastic edges are just vertical and horizontal edges (pairs of closest vertices) and the bending ribs are the vertical or horizontal triples of consecutive (closest) vertices.
- The energy of the elastic map is
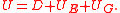
The elastic map should be in the mechanical equilibrium: it should minimise the energy
 .
.Expectation-maximization algorithm
For a given splitting of the dataset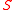 in classes
in classes  minimization of the quadratic functional
minimization of the quadratic functional  is a linear problem with the sparse matrix of coefficients. Therefore, similarly to PCA or k-means, a splitting method is used:
is a linear problem with the sparse matrix of coefficients. Therefore, similarly to PCA or k-means, a splitting method is used:
- For given
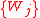 find
find 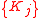 ;
; - For given
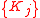 minimize
minimize  and find
and find 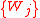 ;
; - If no change, terminate.
This expectation-maximization algorithm
Expectation-maximization algorithm
In statistics, an expectation–maximization algorithm is an iterative method for finding maximum likelihood or maximum a posteriori estimates of parameters in statistical models, where the model depends on unobserved latent variables...
guarantees a local minimum of
 . For improving the approximation various additional methods are proposed. For example, the softening strategy is used. This strategy
. For improving the approximation various additional methods are proposed. For example, the softening strategy is used. This strategystarts with a rigid grids (small length, small bending and large elasticity modules
 and
and  coefficients) and finishes with soft grids (small
coefficients) and finishes with soft grids (small  and
and  ). The training goes in several epochs, each epoch with its own grid rigidness. Another adaptive strategy is growing net: one starts from small amount of nodes and gradually adds new nodes. Each epoch goes with it own number of nodes.
). The training goes in several epochs, each epoch with its own grid rigidness. Another adaptive strategy is growing net: one starts from small amount of nodes and gradually adds new nodes. Each epoch goes with it own number of nodes.Applications
Most important applications are in bioinformatics, for exploratory data analysis and visualisation of multidimensional data, for data visualisation in economics, social and political sciences, as an auxiliary tool for data mapping in geographic informational systems and for visualisation of data of various nature.
Recently, the method is adapted as a support tool in the decision process underlying the selection, optimization, and management of financial portfolios.