
Electromagnetic wave equation
Overview
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
that describes the propagation of electromagnetic waves through a medium
Medium (optics)
An optical medium is material through which electromagnetic waves propagate. It is a form of transmission medium. The permittivity and permeability of the medium define how electromagnetic waves propagate in it...
or in a vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
. The homogeneous
Homogeneous differential equation
The term homogeneous differential equation has several distinct meanings.One meaning is that a first-order ordinary differential equation is homogeneous if it has the formwhere F is a homogeneous function of degree zero; that is to say, that F = F.In a related, but distinct, usage, the term linear...
form of the equation, written in terms of either the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
E or the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
B, takes the form:
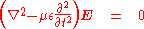
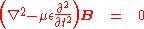
where
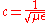
is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in the medium, and ∇2 is the Laplace operator
Vector Laplacian
In mathematics and physics, the vector Laplace operator, denoted by \scriptstyle \nabla^2, named after Pierre-Simon Laplace, is a differential operator defined over a vector field. The vector Laplacian is similar to the scalar Laplacian...
.

