
Vector Laplacian
Encyclopedia
In mathematics
and physics
, the vector Laplace operator, denoted by , named after Pierre-Simon Laplace
, named after Pierre-Simon Laplace
, is a differential operator defined over a vector field
. The vector Laplacian is similar to the scalar Laplacian. Whereas the scalar Laplacian applies to scalar field
and returns a scalar quantity, the vector Laplacian applies to the vector fields and returns a vector quantity. The returned vector field is equal to the vector field of the scalar Laplacian applied on the individual elements.
 is defined as
is defined as
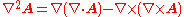
In Cartesian coordinates, this reduces to the much simpler form (This can be seen a special case of Lagrange's formula, see Vector triple product.)
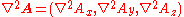
where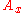 ,
, 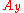 , and
, and  are the components of
are the components of  .
.
For expressions of the vector Laplacian in other coordinate systems see Nabla in cylindrical and spherical coordinates.
 ("tensor" includes scalar and vector) is defined as the divergence
("tensor" includes scalar and vector) is defined as the divergence
of the gradient
of the tensor:

For the special case where is a scalar
is a scalar
(a tensor of rank zero), the Laplacian takes on the familiar form.
If is a vector (a tensor of first rank), the gradient is a covariant derivative
is a vector (a tensor of first rank), the gradient is a covariant derivative
which results in a tensor of second rank, and the divergence of this is again a vector. The formula for the vector Laplacian above may be used to avoid tensor math and may be shown to be equivalent to the divergence of the expression shown below for the gradient of a vector:
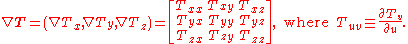
And, in the same manner, a dot product, which evaluates to a vector, of a vector by the gradient of another vector (a tensor of 2nd rank) can be seen as a product of matrices:

for a Newtonian
incompressible flow
:
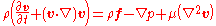
where the term with the vector Laplacian of the velocity
field represents the viscous
represents the viscous
stress
es in the fluid.
Another example is the wave equation for the electric field that can be derived from
the Maxwell equations in the absence of charges and currents:

The previous equation can also be written as:
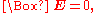
where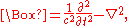
is the D'Alembertian, used in the Klein–Gordon equation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the vector Laplace operator, denoted by
 , named after Pierre-Simon Laplace
, named after Pierre-Simon LaplacePierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
, is a differential operator defined over a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
. The vector Laplacian is similar to the scalar Laplacian. Whereas the scalar Laplacian applies to scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
and returns a scalar quantity, the vector Laplacian applies to the vector fields and returns a vector quantity. The returned vector field is equal to the vector field of the scalar Laplacian applied on the individual elements.
Definition
The vector Laplacian of a vector field is defined as
is defined as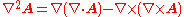
In Cartesian coordinates, this reduces to the much simpler form (This can be seen a special case of Lagrange's formula, see Vector triple product.)
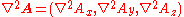
where
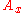 ,
, 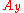 , and
, and  are the components of
are the components of  .
.For expressions of the vector Laplacian in other coordinate systems see Nabla in cylindrical and spherical coordinates.
Generalization
The Laplacian of any tensor fieldTensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
 ("tensor" includes scalar and vector) is defined as the divergence
("tensor" includes scalar and vector) is defined as the divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of the tensor:

For the special case where
 is a scalar
is a scalarScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
(a tensor of rank zero), the Laplacian takes on the familiar form.
If
 is a vector (a tensor of first rank), the gradient is a covariant derivative
is a vector (a tensor of first rank), the gradient is a covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
which results in a tensor of second rank, and the divergence of this is again a vector. The formula for the vector Laplacian above may be used to avoid tensor math and may be shown to be equivalent to the divergence of the expression shown below for the gradient of a vector:
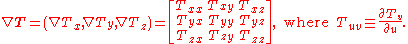
And, in the same manner, a dot product, which evaluates to a vector, of a vector by the gradient of another vector (a tensor of 2nd rank) can be seen as a product of matrices:

Use in physics
An example of the usage of the vector Laplacian is the Navier-Stokes equationsNavier-Stokes equations
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
for a Newtonian
Newtonian fluid
A Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:...
incompressible flow
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
:
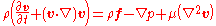
where the term with the vector Laplacian of the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
field
 represents the viscous
represents the viscousViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
es in the fluid.
Another example is the wave equation for the electric field that can be derived from
the Maxwell equations in the absence of charges and currents:

The previous equation can also be written as:
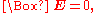
where
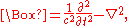
is the D'Alembertian, used in the Klein–Gordon equation.

