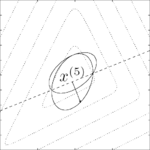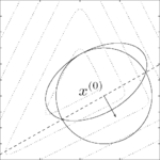
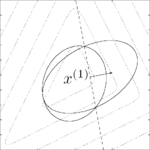
Ellipsoid method
Encyclopedia
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
for minimizing convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
s. When specialized to solving feasible linear optimization problems with rational data, the ellipsoid method is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, which finds an optimal solution in a finite number of steps.
The ellipsoid method generates a sequence of ellipsoids whose volume uniformly decreases at every step, thus enclosing a minimizer of a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
.
History
The ellipsoid method has a long history. As an iterative methodIterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
, a preliminary version was introduced by Naum Z. Shor
Naum Z. Shor
Naum Zuselevich Shor was a Soviet and Ukrainian Jewish mathematician specializing in optimization.He made significant contributions to nonlinear and stochastic programming, numerical techniques for non-smooth optimization, discrete optimization problems, matrix optimization, dual quadratic bounds...
. In 1972, an approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
for real convex minimization was studied by Arkadi Nemirovski
Arkadi Nemirovski
Arkadi Nemirovski is a professor in the H. Milton Stewart School of Industrial and Systems Engineering at Georgia Institute of Technology.Arkadi Nemirovski earned the Ph.D. in Mathematics from Moscow State University and the Doctor of Sciences in Mathematics from the Institute of Cybernetics of...
and David B. Yudin (Judin). As an algorithm for solving linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problems with rational data, the ellipsoid algorithm was studied by Leonid Khachiyan
Leonid Khachiyan
Leonid Genrikhovich Khachiyan was a Soviet mathematician of Armenian descent who taught Computer Science at Rutgers University. He was most famous for his Ellipsoid algorithm for linear programming, which was the first such algorithm known to have a polynomial running time...
: Khachiyan's achievement was to prove the polynomial-time solvability of linear programs.
Following Khachiyan's work, the ellipsoid method was the only algorithm for solving linear programs whose runtime was provably polynomial. However, the interior-point method and variants of the simplex algorithm
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
are much faster than the ellipsoid method in practice. Karmarkar's algorithm is also faster in the worst case.
However, the ellipsoidal algorithm allows complexity theorists
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
to achieve (worst-case) bounds that depend on the dimension of the problem and on the size of the data, but not on the number of rows, so it remains important in combinatorial optimization
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
theory.
Description
A convex minimization problem consists of a convex functionConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
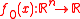 to be minimized over the variable
to be minimized over the variable  , convex inequality constraints of the form
, convex inequality constraints of the form 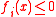 , where the functions
, where the functions 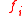 are convex, and linear equality constraints of the form
are convex, and linear equality constraints of the form  . We are also given an initial ellipsoid
. We are also given an initial ellipsoid 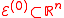 defined as
defined as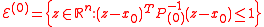
containing a minimizer
 , where
, where  and
and  is the center of
is the center of 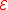 . Finally, we require the existence of a cutting-plane oracle for the function
. Finally, we require the existence of a cutting-plane oracle for the function 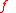 . One example of a cutting-plane is given by a subgradient
. One example of a cutting-plane is given by a subgradient  of
of 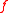 .
.Unconstrained Minimization
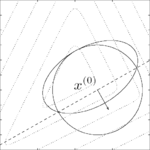
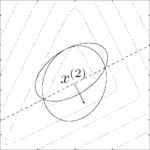
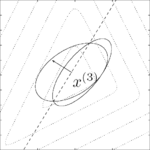
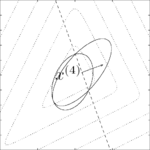
At the -th iteration of the algorithm, we have a point
-th iteration of the algorithm, we have a point 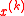 at the center of an ellipsoid
at the center of an ellipsoid 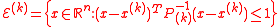 . We query the cutting-plane oracle to obtain a vector
. We query the cutting-plane oracle to obtain a vector 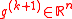 such that
such that 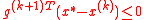 . We therefore conclude that
. We therefore conclude that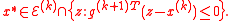
We set
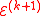 to be the ellipsoid of minimal volume containing the half-ellipsoid described above and compute
to be the ellipsoid of minimal volume containing the half-ellipsoid described above and compute  . The update is given by
. The update is given by
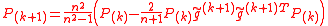
where
 . The stopping criterion is given by the property that
. The stopping criterion is given by the property that
Inequality-Constrained Minimization
At the -th iteration of the algorithm for constrained minimization, we have a point
-th iteration of the algorithm for constrained minimization, we have a point 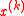 at the center of an ellipsoid
at the center of an ellipsoid 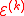 as before. We also must maintain a list of values
as before. We also must maintain a list of values 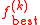 recording the smallest objective value of feasible iterates so far. Depending on whether or not the point
recording the smallest objective value of feasible iterates so far. Depending on whether or not the point 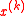 is feasible, we perform one of two tasks:
is feasible, we perform one of two tasks:- If
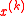 is feasible, perform essentially the same update as in the unconstrained case, by choosing a subgradient
is feasible, perform essentially the same update as in the unconstrained case, by choosing a subgradient 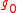 that satisfies
that satisfies
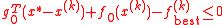
- If
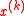 is infeasible and violates the
is infeasible and violates the 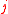 -th constraint, update the ellipsoid with a feasibility cut. Our feasibility cut may be a subgradient
-th constraint, update the ellipsoid with a feasibility cut. Our feasibility cut may be a subgradient 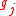 of
of 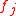 which must satisfy
which must satisfy
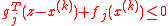
for all feasible
 .
.Performance
The ellipsoid method is used on low-dimensional problems, such as planar location problems, where it is numerically stable. On even "small"-sized problems, it suffers from numerical instability and poor performance in practice.However, the ellipsoid method is an important theoretical technique in combinatorial optimization
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
. In computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, the ellipsoid algorithm is attractive because its complexity depends on the number of columns and the digital size of the coefficients, but not on the number of rows.