Elliptic Curve Diffie-Hellman
Encyclopedia
Elliptic curve Diffie–Hellman (ECDH) is a key agreement protocol that allows two parties, each having an elliptic curve public-private key pair, to establish a shared secret over an insecure channel. This shared secret may be directly used as a key, or better yet, to derive another key
which can then be used to encrypt subsequent communications using a symmetric key cipher. It is a variant of the Diffie–Hellman protocol using elliptic curve cryptography
.
wants to establish a shared key with Bob
, but the only channel available for them may be eavesdropped by a third party. Initially, the domain parameters (that is,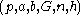
in the prime case or 
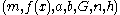in the binary case) must be agreed upon. Also, each party must have a key pair suitable for elliptic curve cryptography, consisting of a private key 
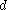(a randomly selected integer in the interval 
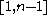) and a public key 
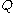(where 
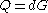). Let Alice's key pair be 
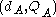and Bob's key pair be 
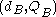. Each party must have the other party's public key (an exchange must occur).
Alice computes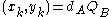
. Bob computes 
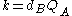. The shared key is 
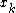(the x coordinate of the point).
The number calculated by both parties is equal, because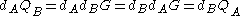
.
The protocol is secure because nothing is disclosed (except for the public keys, which are not secret), and no party can derive the private key of the other unless it can solve the Elliptic Curve Discrete Logarithm
Problem.
The public keys are either static (and trusted, say via a certificate) or ephemeral. Ephemeral keys are not necessarily authenticated, so if authentication is wanted, it has to be obtained by other means. Static public keys provide neither forward secrecy nor key-compromise impersonation resilience, among other advanced security properties. Holders of static private keys should validate the other public key, and should apply a secure key derivation function to the raw Diffie–Hellman shared secret to avoid leaking information about the static private key. For schemes with more advanced security properties see ECMQV.
Key derivation function
In cryptography, a key derivation function derives one or more secret keys from a secret value such as a master key or other known information such as a password or passphrase using a pseudo-random function...
which can then be used to encrypt subsequent communications using a symmetric key cipher. It is a variant of the Diffie–Hellman protocol using elliptic curve cryptography
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
.
Key establishment protocol
Suppose AliceAlice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
wants to establish a shared key with Bob
Alice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
, but the only channel available for them may be eavesdropped by a third party. Initially, the domain parameters (that is,
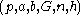in the prime case or 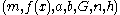in the binary case) must be agreed upon. Also, each party must have a key pair suitable for elliptic curve cryptography, consisting of a private key 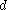(a randomly selected integer in the interval 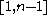) and a public key 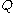(where 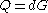). Let Alice's key pair be 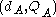and Bob's key pair be 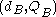. Each party must have the other party's public key (an exchange must occur).Alice computes
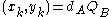. Bob computes 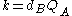. The shared key is 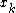(the x coordinate of the point).The number calculated by both parties is equal, because
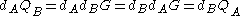.The protocol is secure because nothing is disclosed (except for the public keys, which are not secret), and no party can derive the private key of the other unless it can solve the Elliptic Curve Discrete Logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
Problem.
The public keys are either static (and trusted, say via a certificate) or ephemeral. Ephemeral keys are not necessarily authenticated, so if authentication is wanted, it has to be obtained by other means. Static public keys provide neither forward secrecy nor key-compromise impersonation resilience, among other advanced security properties. Holders of static private keys should validate the other public key, and should apply a secure key derivation function to the raw Diffie–Hellman shared secret to avoid leaking information about the static private key. For schemes with more advanced security properties see ECMQV.