Elliptical distribution
Encyclopedia
In probability
and statistics
, an elliptical distribution is any member of a broad family of probability distribution
s that generalize the multivariate normal distribution and inherit some of its properties.
s. A multivariate distribution is said to be elliptical if its characteristic function is of the form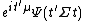
for a specified vector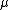
, positive-definite matrix 
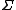, and characteristic function 
. 
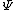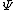is known as the characteristic generator of the elliptical distribution.
Elliptical distributions can also be defined in terms of their density functions. When they exist, the density functions f have the structure:
where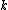
is a scale factor, 
is an 
-dimensional random vector with median vector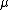 
(which is also the mean vector if the latter exists), 
is a positive definite matrix which is proportional to the covariance matrix if the latter exists, and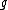 
is a function mapping from the non-negative reals to the non-negative reals giving a finite area under the curve.
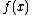) is an ellipse
(hence the name elliptical distribution). More generally, for arbitrary n the iso-density loci are ellipsoids. The density function shows that the distribution is symmetric about its vector mean, a property known as elliptical symmetry.
The multivariate normal distribution is the special case in which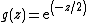
for quadratic form 
. While the multivariate normal is unbounded (each element of 
can take on arbitrarily large positive or negative values with non-zero probability, because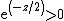 
for all non-negative 
), in general elliptical distributions can be bounded or unbounded—such a distribution is bounded if 
for all 
greater than some value.
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, an elliptical distribution is any member of a broad family of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s that generalize the multivariate normal distribution and inherit some of its properties.
Definition
Elliptical distributions can be defined using characteristic functionCharacteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
s. A multivariate distribution is said to be elliptical if its characteristic function is of the form
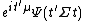
for a specified vector
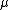, positive-definite matrix 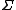, and characteristic function 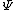. 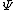is known as the characteristic generator of the elliptical distribution.Elliptical distributions can also be defined in terms of their density functions. When they exist, the density functions f have the structure:
where
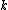is a scale factor, is an -dimensional random vector with median vector 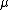(which is also the mean vector if the latter exists), is a positive definite matrix which is proportional to the covariance matrix if the latter exists, and 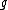is a function mapping from the non-negative reals to the non-negative reals giving a finite area under the curve.Properties
In the 2-dimensional case where the density exists, each iso-density locus (the set of x1,x2 pairs all giving a particular value of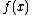) is an ellipseEllipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
(hence the name elliptical distribution). More generally, for arbitrary n the iso-density loci are ellipsoids. The density function shows that the distribution is symmetric about its vector mean, a property known as elliptical symmetry.
The multivariate normal distribution is the special case in which
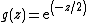for quadratic form . While the multivariate normal is unbounded (each element of can take on arbitrarily large positive or negative values with non-zero probability, because 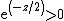for all non-negative ), in general elliptical distributions can be bounded or unbounded—such a distribution is bounded if for all greater than some value.