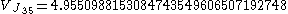Elongated triangular orthobicupola
Encyclopedia
In geometry
, the elongated triangular orthobicupola is one of the Johnson solid
s (J35). As the name suggests, it can be constructed by elongating a triangular orthobicupola
(J27) by inserting a hexagonal prism
between its two halves. The resulting solid is superficially similar to the rhombicuboctahedron
(one of the Archimedean solid
s), with the difference that it has threefold rotational symmetry about its axis instead of fourfold symmetry.
The 92 Johnson solids were named and described by Norman Johnson in 1966.
J35 consists of 2 cupolae and hexagonal prism.
The two cupolae makes 1 cuboctahedron = 8 tetrahedra + 6 half-octahedra.
1 octahedron = 4 tetrahedra, so total we have 20 tetrahedra.
What is the volume of a tetrahedron?
Construct a tetrahedron having vertices in common with alternate vertices of a
cube (of side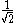 , if tetrahedron has unit edges). The 4 triangular
, if tetrahedron has unit edges). The 4 triangular
pyramids left if the tetrahedron is removed from the cube form half an
octahedron = 2 tetrahedra. So
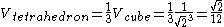
The hexagonal prism is more straightforward. The hexagon has area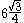 , so
, so
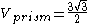
Finally
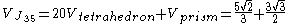
numerical value:
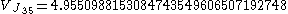
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the elongated triangular orthobicupola is one of the Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s (J35). As the name suggests, it can be constructed by elongating a triangular orthobicupola
Triangular orthobicupola
In geometry, the triangular orthobicupola is one of the Johnson solids . As the name suggests, it can be constructed by attaching two triangular cupolas along their bases...
(J27) by inserting a hexagonal prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
between its two halves. The resulting solid is superficially similar to the rhombicuboctahedron
Rhombicuboctahedron
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...
(one of the Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s), with the difference that it has threefold rotational symmetry about its axis instead of fourfold symmetry.
The 92 Johnson solids were named and described by Norman Johnson in 1966.
Volume
The volume of J35 can be calculated as follows:J35 consists of 2 cupolae and hexagonal prism.
The two cupolae makes 1 cuboctahedron = 8 tetrahedra + 6 half-octahedra.
1 octahedron = 4 tetrahedra, so total we have 20 tetrahedra.
What is the volume of a tetrahedron?
Construct a tetrahedron having vertices in common with alternate vertices of a
cube (of side
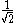 , if tetrahedron has unit edges). The 4 triangular
, if tetrahedron has unit edges). The 4 triangularpyramids left if the tetrahedron is removed from the cube form half an
octahedron = 2 tetrahedra. So
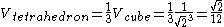
The hexagonal prism is more straightforward. The hexagon has area
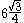 , so
, so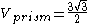
Finally
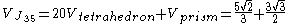
numerical value: