
Empty sum
Encyclopedia
In mathematics
, an empty sum, or nullary sum, is a summation
involving no terms at all. The value of any empty sum of numbers is conventionally taken to be zero
. For summations defined in terms of addition of other values than numbers (such as vectors, matrices
, polynomial
s), in general of values in some given Abelian group
, the value of an empty summation is taken to be the zero element
of that group.
An empty sum can arise in particular for expressions of the form

when a > b; in such case the summation has value 0 (or the zero element of the additive group in which the terms ti live).
A situation similar to an empty summation can arise for other operations than addition; notably, its counterpart for multiplication
is an empty product
, a product
of no factors at all. In such cases the convention of a zero result does not apply; indeed the value of an empty product of numbers is taken to be one, the neutral element for multiplication.
, since that operation requires exactly two operands. The need to consider empty sums arises with summation: the process of "adding together" a collection of values that can have an arbitrary size. For a finite collection of two or more numbers, the commutative and associative laws of addition imply that every expression formed using addition only, and in which all members of the collection appear exactly once as operand, has the same value; this defines the sum
of the collection. For infinite collections of values this definition does not apply, as no (finite) expression can combine them all using addition operations; the notion of a series
can be used to attach a definite sum to some infinite collections, but this requires more than addition only, notably some notion of limit
.
This leaves the cases of collections with less than two elements. One could decide to leave the sum of such collections undefined, on the grounds that there are too few values to perform any addition. For various reasons it is however useful to not make such an exception, and define the sum of any finite collection of values. Doing so should be done without invalidating the usual properties of summation, notably the fact that adjoining a new value x to a collection adds x to the sum of the collection. This property then implies that the sum of a collection containing a single value v is v, and that the sum of a collection of no values at all is 0, the neutral element for addition. An alternative approach is to define the sum of a finite sequence of values by induction on its length, with as starting case the empty sequence whose sum is 0. Both approaches define the same notion of sum, and the latter does so without making any separate definition for an empty sum.
and the empty set
in the first place: while they seem to represent quite uninteresting notions, their existence allows for a much cleaner mathematical presentation of many subjects.
An even stronger case for the definition of empty sums arises when certain notions are defined in terms the existence of summations; not defining empty sums would implicitly alter such notions in a way that is usually undesirable. For instance in number theory
, a partition
of an integer n can be defined as a weakly decreasing sequence of positive integers whose sum is n. It is important that there is exactly one partition of the number 0 (most formulas for counting partitions would break down if there were assumed to be no partitions of 0), and since terms must be positive, the empty sequence is the only possible candidate. More generally, it often happens in combinatorics
that certain values are considered to be a member of a given class by virtue of an empty sum, for instance 0 is a triangular number
because of
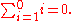
does provide one such example in the form of empty linear combination
s. One characterization of a linearly dependent set is that one of its elements can be written as a linear combination of the other elements; if this is to apply to the linearly dependent set containing just the zero vector, it must be that the zero vector is a linear combination of no vectors at all, which is an empty sum of vectors. Also every finite dimensional vector space admits a basis
, whose number of elements is equal to the dimension, and every element of the vector space can be uniquely expressed as linear combination of basis vectors. Applying this to a space of dimension 0, which contains exactly one vector (the zero vector), the only candidate for a basis is the empty set (both because 0 elements are required, and because the zero vector cannot be in any basis). Then the zero vector of this space can be expressed as a linear combination of no elements, which again is an empty sum.
that describes the terms of a summation, even if the range of summation happens to be empty. Since this expression is never instantiated in an empty sum, its value is irrelevant; for instance the harmonic number

is perfectly well defined. However, the kind of values denoted by the summand is of importance for the value of the summation; for instance, an empty summation of elements of a vector space
has as value the zero vector in that space, rather than the number 0. Even more important is the fact that the operation is summation; by contrast, the empty product
—a product
of no factors at all—has as value of one.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an empty sum, or nullary sum, is a summation
Summation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
involving no terms at all. The value of any empty sum of numbers is conventionally taken to be zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
. For summations defined in terms of addition of other values than numbers (such as vectors, matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s), in general of values in some given Abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, the value of an empty summation is taken to be the zero element
Zero element
In mathematics, a zero element is one of several generalizations of the number zero to other algebraic structures. These alternate meanings may or may not reduce to the same thing, depending on the context.-Additive identities:...
of that group.
An empty sum can arise in particular for expressions of the form

when a > b; in such case the summation has value 0 (or the zero element of the additive group in which the terms ti live).
A situation similar to an empty summation can arise for other operations than addition; notably, its counterpart for multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
is an empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
, a product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of no factors at all. In such cases the convention of a zero result does not apply; indeed the value of an empty product of numbers is taken to be one, the neutral element for multiplication.
Summation convention
Empty sums, or even sums of a single term, do not play a role in the definition of additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, since that operation requires exactly two operands. The need to consider empty sums arises with summation: the process of "adding together" a collection of values that can have an arbitrary size. For a finite collection of two or more numbers, the commutative and associative laws of addition imply that every expression formed using addition only, and in which all members of the collection appear exactly once as operand, has the same value; this defines the sum
SUM
SUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
of the collection. For infinite collections of values this definition does not apply, as no (finite) expression can combine them all using addition operations; the notion of a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
can be used to attach a definite sum to some infinite collections, but this requires more than addition only, notably some notion of limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
.
This leaves the cases of collections with less than two elements. One could decide to leave the sum of such collections undefined, on the grounds that there are too few values to perform any addition. For various reasons it is however useful to not make such an exception, and define the sum of any finite collection of values. Doing so should be done without invalidating the usual properties of summation, notably the fact that adjoining a new value x to a collection adds x to the sum of the collection. This property then implies that the sum of a collection containing a single value v is v, and that the sum of a collection of no values at all is 0, the neutral element for addition. An alternative approach is to define the sum of a finite sequence of values by induction on its length, with as starting case the empty sequence whose sum is 0. Both approaches define the same notion of sum, and the latter does so without making any separate definition for an empty sum.
Relevance of defining empty sums
The necessity to define a value for empty summations is not immediately obvious, as it may appear strange to set up a summation when there is nothing to add. However empty summations often arise implicitly when the range of values being added depends on certain unknown parameters, and may become empty for certain values of the parameters. Leaving the value of an empty summation undefined would make it hard to make certain definitions properly, requiring frequent consideration of special cases to avoid empty sums. It would also imply an additional effort required in the proof of any statement involving summations to ensure that they never involve empty summations. In fact the reasons for defining empty sums are very similar to the reasons to considering things like the number zero0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
and the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
in the first place: while they seem to represent quite uninteresting notions, their existence allows for a much cleaner mathematical presentation of many subjects.
An even stronger case for the definition of empty sums arises when certain notions are defined in terms the existence of summations; not defining empty sums would implicitly alter such notions in a way that is usually undesirable. For instance in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a partition
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of an integer n can be defined as a weakly decreasing sequence of positive integers whose sum is n. It is important that there is exactly one partition of the number 0 (most formulas for counting partitions would break down if there were assumed to be no partitions of 0), and since terms must be positive, the empty sequence is the only possible candidate. More generally, it often happens in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
that certain values are considered to be a member of a given class by virtue of an empty sum, for instance 0 is a triangular number
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
because of
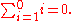
An example: empty linear combinations
Outside combinatorics, additive decompositions occur less frequently than multiplicative ones, which makes this kind of argument for defining empty sums less obvious than similar arguments for empty products. However linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
does provide one such example in the form of empty linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s. One characterization of a linearly dependent set is that one of its elements can be written as a linear combination of the other elements; if this is to apply to the linearly dependent set containing just the zero vector, it must be that the zero vector is a linear combination of no vectors at all, which is an empty sum of vectors. Also every finite dimensional vector space admits a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, whose number of elements is equal to the dimension, and every element of the vector space can be uniquely expressed as linear combination of basis vectors. Applying this to a space of dimension 0, which contains exactly one vector (the zero vector), the only candidate for a basis is the empty set (both because 0 elements are required, and because the zero vector cannot be in any basis). Then the zero vector of this space can be expressed as a linear combination of no elements, which again is an empty sum.
Significance of "terms" of an empty sum
Since an empty sum by definition has no terms, it seems contradictory to talk about its terms; however in practice there almost always is an expressionExpression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
that describes the terms of a summation, even if the range of summation happens to be empty. Since this expression is never instantiated in an empty sum, its value is irrelevant; for instance the harmonic number

is perfectly well defined. However, the kind of values denoted by the summand is of importance for the value of the summation; for instance, an empty summation of elements of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
has as value the zero vector in that space, rather than the number 0. Even more important is the fact that the operation is summation; by contrast, the empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
—a product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of no factors at all—has as value of one.

