Energy drift
Encyclopedia
In molecular dynamics
, orbit, and particle simulations, energy drift is the gradual change in the total energy of a closed system. According to the laws of mechanics, the energy should be a constant of motion
and should not change. However, the energy does fluctuate on a short time scale and increase on a very long time scale due to numerical integration
artifacts that arise with the use of a finite time step Δt. More specifically, the energy tends to increase exponentially; its increase can be understood intuitively because each step introduces a small perturbation δv to the true velocity vtrue, which (if uncorrelated with v) results in a second-order increase in the energy
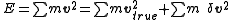
(The cross term in v · δv is zero because of no correlation.)
Energy drift - usually damping - is substantial for numerical integration schemes that are not symplectic
, such as the Runge-Kutta family. Symplectic integrators usually used in molecular dynamics, such as the Verlet integrator
family, exhibit increases in energy over very long time scales, though the error remains roughly constant. These integrators do not in fact reproduce the actual Hamiltonian mechanics
of the system; instead, they reproduce a closely related "shadow" Hamiltonian whose value they conserve many orders of magnitude more closely. The accuracy of the energy conservation for the true Hamiltonian is dependent on the time step. The energy computed from the modified Hamiltonian of a symplectic integrator is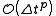
from the true Hamiltonian.
Energy drift is similar to parametric resonance in that a finite, discrete timestepping scheme will result in nonphysical, limited sampling of motions with frequencies
close to the frequency of velocity updates. Thus the restriction on the maximum step size that will be stable for a given system is proportional to the period of the fastest fundamental modes of the system's motion. For a motion with a natural frequency ω, artificial resonances are introduced when the frequency of velocity updates,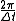
is related to ω as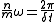
where n and m are integers describing the resonance order. For Verlet integration, resonances up to the fourth order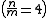
frequently lead to numerical instability, leading to a restriction on the timestep size of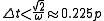
where ω is the frequency of the fastest motion in the system and p is its period. The fastest motions in most biomolecular systems involve the motions of hydrogen
atoms; it is thus common to use constraint algorithm
s to restrict hydrogen motion and thus increase the maximum stable time step that can be used in the simulation. However, because the time scales of heavy-atom motions are not widely divergent from those of hydrogen motions, in practice this allows only about a twofold increase in time step. Common practice in all-atom biomolecular simulation is to use a time step of 1 femtosecond (fs) for unconstrained simulations and 2 fs for constrained simulations, although larger time steps may be possible for certain systems or choices of parameters.
Energy drift can also result from imperfections in evaluating the energy function
, usually due to simulation parameters that sacrifice accuracy for computational speed. For example, cutoff schemes for evaluating the electrostatic forces introduce systematic errors in the energy with each time step as particles move back and forth across the cutoff radius if sufficient smoothing is not used. Particle mesh Ewald summation is one solution for this effect, but introduces artifacts of its own. Errors in the system being simulated can also induce energy drifts characterized as "explosive" that are not artifacts, but are reflective of the instability of the initial conditions; this may occur when the system has not been subjected to sufficient structural minimization before beginning production dynamics. In practice, energy drift may be measured as a percent increase over time, or as a time needed to add a given amount of energy to the system. The practical effects of energy drift depend on the simulation conditions, the thermodynamic ensemble being simulated, and the intended use of the simulation under study; for example, energy drift has much more severe consequences for simulations of the microcanonical ensemble
than the canonical ensemble
where the temperature is held constant. Energy drift is often used as a measure of the quality of the simulation, and has been proposed as one quality metric to be routinely reported in a mass repository of molecular dynamics trajectory data analogous to the Protein Data Bank
.
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
, orbit, and particle simulations, energy drift is the gradual change in the total energy of a closed system. According to the laws of mechanics, the energy should be a constant of motion
Constant of motion
In mechanics, a constant of motion is a quantity that is conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a mathematical constraint, the natural consequence of the equations of motion, rather than a physical constraint...
and should not change. However, the energy does fluctuate on a short time scale and increase on a very long time scale due to numerical integration
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
artifacts that arise with the use of a finite time step Δt. More specifically, the energy tends to increase exponentially; its increase can be understood intuitively because each step introduces a small perturbation δv to the true velocity vtrue, which (if uncorrelated with v) results in a second-order increase in the energy
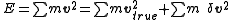
(The cross term in v · δv is zero because of no correlation.)
Energy drift - usually damping - is substantial for numerical integration schemes that are not symplectic
Symplectic integrator
In mathematics, a symplectic integrator is a numerical integration scheme for a specific group of differential equations related to classical mechanics and symplectic geometry. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations...
, such as the Runge-Kutta family. Symplectic integrators usually used in molecular dynamics, such as the Verlet integrator
Verlet integration
Verlet integration is a numerical method used to integrate Newton's equations of motion. It is frequently used to calculate trajectories of particles in molecular dynamics simulations and computer graphics...
family, exhibit increases in energy over very long time scales, though the error remains roughly constant. These integrators do not in fact reproduce the actual Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
of the system; instead, they reproduce a closely related "shadow" Hamiltonian whose value they conserve many orders of magnitude more closely. The accuracy of the energy conservation for the true Hamiltonian is dependent on the time step. The energy computed from the modified Hamiltonian of a symplectic integrator is
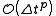from the true Hamiltonian.Energy drift is similar to parametric resonance in that a finite, discrete timestepping scheme will result in nonphysical, limited sampling of motions with frequencies
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
close to the frequency of velocity updates. Thus the restriction on the maximum step size that will be stable for a given system is proportional to the period of the fastest fundamental modes of the system's motion. For a motion with a natural frequency ω, artificial resonances are introduced when the frequency of velocity updates,
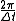is related to ω as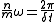where n and m are integers describing the resonance order. For Verlet integration, resonances up to the fourth order
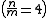frequently lead to numerical instability, leading to a restriction on the timestep size of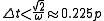where ω is the frequency of the fastest motion in the system and p is its period. The fastest motions in most biomolecular systems involve the motions of hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
atoms; it is thus common to use constraint algorithm
Constraint algorithm
In mechanics, a constraint algorithm is a method for satisfying constraints for bodies that obey Newton's equations of motion. There are three basic approaches to satisfying such constraints: choosing novel unconstrained coordinates , introducing explicit constraint forces, and minimizing...
s to restrict hydrogen motion and thus increase the maximum stable time step that can be used in the simulation. However, because the time scales of heavy-atom motions are not widely divergent from those of hydrogen motions, in practice this allows only about a twofold increase in time step. Common practice in all-atom biomolecular simulation is to use a time step of 1 femtosecond (fs) for unconstrained simulations and 2 fs for constrained simulations, although larger time steps may be possible for certain systems or choices of parameters.
Energy drift can also result from imperfections in evaluating the energy function
Potential function
The term potential function may refer to:* A mathematical function whose values are a physical potential.* The class of functions known as harmonic functions, which are the topic of study in potential theory.* The potential function of a potential game....
, usually due to simulation parameters that sacrifice accuracy for computational speed. For example, cutoff schemes for evaluating the electrostatic forces introduce systematic errors in the energy with each time step as particles move back and forth across the cutoff radius if sufficient smoothing is not used. Particle mesh Ewald summation is one solution for this effect, but introduces artifacts of its own. Errors in the system being simulated can also induce energy drifts characterized as "explosive" that are not artifacts, but are reflective of the instability of the initial conditions; this may occur when the system has not been subjected to sufficient structural minimization before beginning production dynamics. In practice, energy drift may be measured as a percent increase over time, or as a time needed to add a given amount of energy to the system. The practical effects of energy drift depend on the simulation conditions, the thermodynamic ensemble being simulated, and the intended use of the simulation under study; for example, energy drift has much more severe consequences for simulations of the microcanonical ensemble
Microcanonical ensemble
In statistical physics, the microcanonical ensemble is a theoretical tool used to describe the thermodynamic properties of an isolated system. In such a system, the possible macrostates of the system all have the same energy and the probability for the system to be in any given microstate is the same...
than the canonical ensemble
Canonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
where the temperature is held constant. Energy drift is often used as a measure of the quality of the simulation, and has been proposed as one quality metric to be routinely reported in a mass repository of molecular dynamics trajectory data analogous to the Protein Data Bank
Protein Data Bank
The Protein Data Bank is a repository for the 3-D structural data of large biological molecules, such as proteins and nucleic acids....
.
Further reading
- Sanz-Serna JM, Calvo MP. (1994). Numerical Hamiltonian Problems. Chapman & Hall, London, England.