Canonical ensemble
Encyclopedia
The canonical ensemble in statistical mechanics
is a statistical ensemble representing a probability distribution
of microscopic states of the system. For a system taking only discrete values of energy, the probability distribution is characterised by the probability
of finding the system in a particular microscopic state 
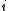with energy level 
, given by Boltzmann distribution
,
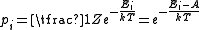
where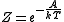
is the normalizing constant
explained below (A is the Helmholtz free energy
function). Boltzmann distribution describes a system that can exchange energy with a heat bath (or alternatively with a large number of similar systems) so that its temperature remains constant. Equivalently, it is the distribution which has maximum entropy for a given average energy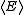
.
It is also referred to as the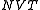
ensemble: the number of particles 
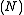, the volume 
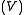, of each system in the ensemble are constant, and the ensemble has a well-defined temperature 
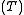, given by the temperature of the heat bath with which it would be in equilibrium.
The quantity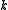
is the Boltzmann constant, which relates the units of temperature to units of energy. It may be suppressed by expressing the absolute temperature using thermodynamic beta,
.
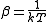The quantities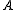
and 
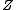are constants for a particular ensemble, which ensure that 
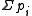is normalised to 1. 
is therefore given by
.
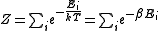This is called the partition function
of the canonical ensemble. Specifying this dependence of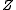
on the energies 
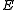conveys the same mathematical information as specifying the form of 
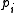above.
The canonical ensemble (and its partition function) is widely used as a tool to calculate thermodynamic quantities of a system under a fixed temperature. This article derives some basic elements of the canonical ensemble. Other related thermodynamic formulas are given in the partition function
article. When viewed in a more general setting, the canonical ensemble is known as the Gibbs measure
, where, because it has the Markov property
of statistical independence, it occurs in many settings outside of the field of physics.
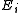be the energy of the microstate
and suppose there are 
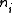members of the ensemble residing in this state. Further we assume the total number of members in the ensemble, 
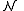, and the total energy of all systems of the ensemble, 
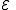, are fixed, i.e.,
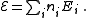
Since systems in the ensemble are distinguishable, for each set
, the number of ways of shuffling systems is equal to
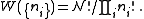
So for a given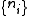
, there are 
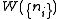rearrangements that specify the same state of the ensemble.
The most probable distribution is the one that maximizes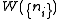
.
The probability for any other distribution to occur is extremely small in the limit
.
To determine this distribution, one should maximize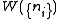
with respect to the 
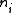's, under two constraints specified above. This can be done by using two Lagrange multipliers
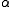and 
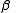. (The assumption that 
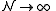would be invoked in such calculation, which allows one to apply Stirling's approximation
.) The result is
.
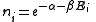This distribution is called the canonical distribution. To determine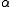
and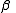 
, it is useful to introduce the partition function
as a sum over microscopic states
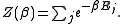
Comparing with thermodynamic formulae, it can be shown that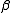
, is related to the absolute temperature 
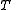as, 
. Moreover the expression
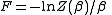
is identified as the Helmholtz free energy
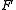. A derivation is given here. Consequently, from the partition function we can obtain the average thermodynamic quantities for the ensemble. For example, the average energy among members of the ensemble is
.
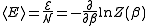This relation can be used to determine
. 
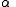is determined from
.
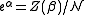Define the following:
It is assumed that the system S and the reservoir S′ are in thermal equilibrium. The objective is to calculate the set of probabilities pm that S is in a particular energy state Em.
Suppose S is in a microstate indexed by m. From the above definitions, the total energy of the system S* is given by
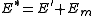
Notice E* is constant, since the combined system S* is taken to be isolated.
Now, arguably the key step in the derivation is that the probability of S being in the m-th state,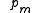
, is proportional to the corresponding number of microstates available to the reservoir when S is in the m-th state. Therefore,
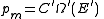
for some constant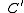
. Taking the logarithm gives
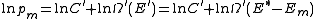
Since Em is small compared to E*, a Taylor series
expansion can be performed on the latter logarithm around the energy E*. A good approximation can be obtained by keeping the first two terms of the Taylor series
expansion:
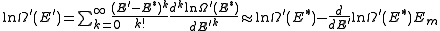
The following quantity is a constant which is traditionally denoted by β, known as the thermodynamic beta.
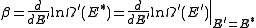
Finally,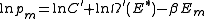
Exponentiating this expression gives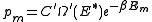
The factor in front of the exponential can be treated as a normalization constant C, where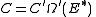
From this
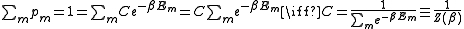
where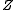
is known as the Partition function
for the canonical ensemble.
:
and obtain the same result. See the article on Maxwell-Boltzmann statistics where this approach is employed.
The canonical ensemble is also called the Gibbs ensemble, in honor of J.W. Gibbs, widely regarded with Boltzmann as being one of the two fathers of statistical mechanics. In his definitive 1901 book "Elementary Principles in Statistical Mechanics", Gibbs viewed an ensemble as a list of the allowed states of the system (each state appearing once and only once in the list) and the associated statistical weights. The states do not interact with each other, or with a reservoir, until Gibbs treats what happens when two complete ensembles at two different temperatures are allowed to interact weakly (Gibbs, pp 160). Gibbs writes that "...the distribution in phase..." (the phase space density in modern language) "...[is] called canonical...[if] the index of probability" (the logarithm of the statistical weight of the phase space density) "...is a linear function of the energy..." (Gibbs, Ch. 4). In Gibbs' formulation, this requirement (his equation 91), in modern notation
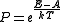
is taken to define the canonical ensemble and to be the fundamental postulate. Gibbs does show that a large collection of interacting microcanonical systems approaches the canonical ensemble, but this is part of his demonstration (Gibbs, pp 169-183) that the principle of equal a priori probabilities, therefore the microcanonical ensemble, are inferior to the canonical ensemble as an axiomatization of statistical mechanics, at every point where the two treatments differ.
Gibbs original formulation is still standard in modern mathematically rigorous treatments of statistical mechanics, where the canonical ensemble is defined as the probability measure
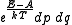
with p and q being the canonical coordinates.
of the canonical ensemble is the Helmholtz free energy
function, as the following relationship holds:
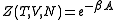
. Suppose the Hamiltonian H of interest is a self adjoint operator with only discrete spectrum
. The energy levels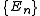
are then the eigenvalues of H, corresponding to eigenvector 
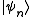. From the same considerations as in the classical case, the probability that a system from the ensemble will be in state 
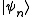is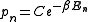 
, for some constant 
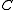. So the ensemble is described by the density matrix
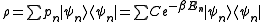
(Technical note: a density matrix must be trace-class, therefore we have also assumed that the sequence of energy eigenvalues diverges sufficiently fast.) A density operator is assumed to have trace 1, so
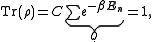
which means
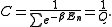
Q is the quantum-mechanical version of the canonical partition function. Putting C back into the equation for ρ gives
By the assumption that the energy eigenvalues diverge, the Hamiltonian H is an unbounded operator
, therefore we have invoked the Borel functional calculus
to exponentiate the Hamiltonian H. Alternatively, in non-rigorous fashion, one can consider that to be the exponential power series.
Notice the quantity
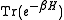
is the quantum mechanical counterpart of the canonical partition function, being the normalization factor for the mixed state of interest.
The density operator ρ obtained above therefore describes the (mixed) state of a canonical ensemble of quantum mechanical systems. As with any density operator, if A is a physical observable, then its expected value is
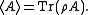
, in which the systems may share particles as well as energy. By contrast, in the microcanonical ensemble
, the energy of each individual system is fixed.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
is a statistical ensemble representing a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of microscopic states of the system. For a system taking only discrete values of energy, the probability distribution is characterised by the probability
of finding the system in a particular microscopic state with energy level , given by Boltzmann distributionBoltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
,
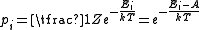
where
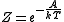
is the normalizing constant
Normalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
explained below (A is the Helmholtz free energy
Helmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
function). Boltzmann distribution describes a system that can exchange energy with a heat bath (or alternatively with a large number of similar systems) so that its temperature remains constant. Equivalently, it is the distribution which has maximum entropy for a given average energy
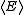.It is also referred to as the
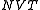ensemble: the number of particles 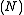, the volume 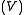, of each system in the ensemble are constant, and the ensemble has a well-defined temperature 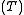, given by the temperature of the heat bath with which it would be in equilibrium.The quantity
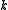is the Boltzmann constant, which relates the units of temperature to units of energy. It may be suppressed by expressing the absolute temperature using thermodynamic beta,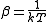.The quantities
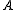and 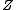are constants for a particular ensemble, which ensure that 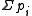is normalised to 1. 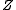is therefore given by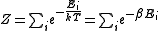.This is called the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
of the canonical ensemble. Specifying this dependence of
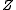on the energies 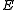conveys the same mathematical information as specifying the form of 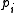above.The canonical ensemble (and its partition function) is widely used as a tool to calculate thermodynamic quantities of a system under a fixed temperature. This article derives some basic elements of the canonical ensemble. Other related thermodynamic formulas are given in the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
article. When viewed in a more general setting, the canonical ensemble is known as the Gibbs measure
Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
, where, because it has the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
of statistical independence, it occurs in many settings outside of the field of physics.
Deriving the Boltzmann factor from ensemble theory
Let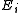 be the energy of the microstateMicrostate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
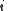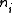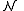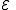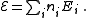
and suppose there are members of the ensemble residing in this state. Further we assume the total number of members in the ensemble, , and the total energy of all systems of the ensemble, , are fixed, i.e.,Since systems in the ensemble are distinguishable, for each set
, the number of ways of shuffling systems is equal to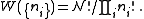So for a given
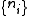, there are 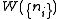rearrangements that specify the same state of the ensemble.The most probable distribution is the one that maximizes
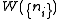.The probability for any other distribution to occur is extremely small in the limit
.To determine this distribution, one should maximize
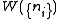with respect to the 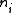's, under two constraints specified above. This can be done by using two Lagrange multipliersLagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
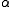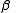and . (The assumption that 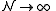would be invoked in such calculation, which allows one to apply Stirling's approximationStirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
.) The result is
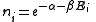.This distribution is called the canonical distribution. To determine
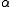and 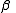, it is useful to introduce the partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
as a sum over microscopic states
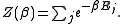
Comparing with thermodynamic formulae, it can be shown that
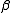, is related to the absolute temperature 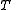as, . Moreover the expression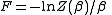is identified as the Helmholtz free energy
Helmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
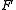. A derivation is given here. Consequently, from the partition function we can obtain the average thermodynamic quantities for the ensemble. For example, the average energy among members of the ensemble is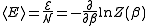.This relation can be used to determine
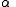. is determined from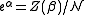.A derivation from heat-bath viewpoint
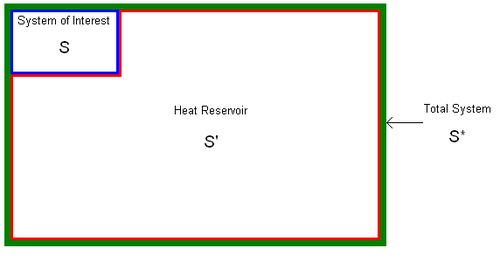
- S - the system of interest
- S′ - the heat reservoir in which S resides; S is small compared to S′
- S* - the system consisting of S and S′ combined together
- m - an indexing variable which labels all the available energy states of the system S
- Em - the energy of the state corresponding to the index m for the system S
- E′ - the energy associated with the heat bath
- E* - the energy associated with S*
- Ω′(E) - denotes the number of microstates available at a particular energy E for the heat reservoir.
It is assumed that the system S and the reservoir S′ are in thermal equilibrium. The objective is to calculate the set of probabilities pm that S is in a particular energy state Em.
Suppose S is in a microstate indexed by m. From the above definitions, the total energy of the system S* is given by
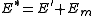
Notice E* is constant, since the combined system S* is taken to be isolated.
Now, arguably the key step in the derivation is that the probability of S being in the m-th state,
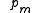, is proportional to the corresponding number of microstates available to the reservoir when S is in the m-th state. Therefore,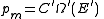for some constant
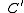. Taking the logarithm gives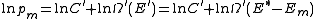Since Em is small compared to E*, a Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion can be performed on the latter logarithm around the energy E*. A good approximation can be obtained by keeping the first two terms of the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion:
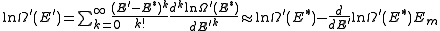
The following quantity is a constant which is traditionally denoted by β, known as the thermodynamic beta.
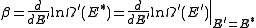
Finally,
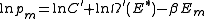
Exponentiating this expression gives
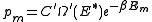
The factor in front of the exponential can be treated as a normalization constant C, where
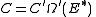
From this
Normalization to recover the partition function
Since probabilities must sum to 1, it must be the case that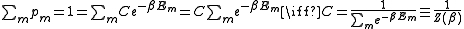where
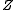is known as the Partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
for the canonical ensemble.
Note on derivation
As mentioned above, the derivation hinges on recognizing that the probability of the system being in a particular state is proportional to the corresponding multiplicities of the reservoir (the same can be said for the grand canonical ensemble). As long as one makes that observation, it is flexible as how one might proceed. In the derivation given, the logarithm is taken, then a linear approximation based on physical arguments is used. Alternatively, one can apply the thermodynamic identity for differential entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
:
and obtain the same result. See the article on Maxwell-Boltzmann statistics where this approach is employed.
The canonical ensemble is also called the Gibbs ensemble, in honor of J.W. Gibbs, widely regarded with Boltzmann as being one of the two fathers of statistical mechanics. In his definitive 1901 book "Elementary Principles in Statistical Mechanics", Gibbs viewed an ensemble as a list of the allowed states of the system (each state appearing once and only once in the list) and the associated statistical weights. The states do not interact with each other, or with a reservoir, until Gibbs treats what happens when two complete ensembles at two different temperatures are allowed to interact weakly (Gibbs, pp 160). Gibbs writes that "...the distribution in phase..." (the phase space density in modern language) "...[is] called canonical...[if] the index of probability" (the logarithm of the statistical weight of the phase space density) "...is a linear function of the energy..." (Gibbs, Ch. 4). In Gibbs' formulation, this requirement (his equation 91), in modern notation
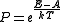
is taken to define the canonical ensemble and to be the fundamental postulate. Gibbs does show that a large collection of interacting microcanonical systems approaches the canonical ensemble, but this is part of his demonstration (Gibbs, pp 169-183) that the principle of equal a priori probabilities, therefore the microcanonical ensemble, are inferior to the canonical ensemble as an axiomatization of statistical mechanics, at every point where the two treatments differ.
Gibbs original formulation is still standard in modern mathematically rigorous treatments of statistical mechanics, where the canonical ensemble is defined as the probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
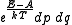
with p and q being the canonical coordinates.
Characteristic state function
The characteristic state functionCharacteristic state function
The characteristic state function in statistical mechanics refers to a particular relationship between the partition function of an ensemble.In particular, if the partition function P satisfiesP = \exp or P = \exp...
of the canonical ensemble is the Helmholtz free energy
Helmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
function, as the following relationship holds:
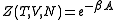
Quantum mechanical systems
By applying the canonical partition function, one can easily obtain the corresponding results for a canonical ensemble of quantum mechanical systems. A quantum mechanical ensemble in general is described by a density matrixDensity matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
. Suppose the Hamiltonian H of interest is a self adjoint operator with only discrete spectrum
Discrete spectrum
In physics, an elementary explanation of a discrete spectrum is that it is an emission spectrum or absorption spectrum for which there is only an integer number of intensities. Atomic electronic absorption and emission spectrum are discrete, as contrasted with, for example, the emission spectrum...
. The energy levels
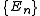are then the eigenvalues of H, corresponding to eigenvector 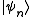. From the same considerations as in the classical case, the probability that a system from the ensemble will be in state 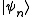is 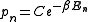, for some constant 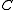. So the ensemble is described by the density matrix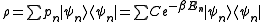(Technical note: a density matrix must be trace-class, therefore we have also assumed that the sequence of energy eigenvalues diverges sufficiently fast.) A density operator is assumed to have trace 1, so
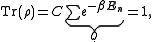
which means
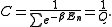
Q is the quantum-mechanical version of the canonical partition function. Putting C back into the equation for ρ gives
By the assumption that the energy eigenvalues diverge, the Hamiltonian H is an unbounded operator
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
, therefore we have invoked the Borel functional calculus
Borel functional calculus
In functional analysis, a branch of mathematics, the Borel functional calculus is a functional calculus , which has particularly broad scope. Thus for instance if T is an operator, applying the squaring function s → s2 to T yields the operator T2...
to exponentiate the Hamiltonian H. Alternatively, in non-rigorous fashion, one can consider that to be the exponential power series.
Notice the quantity
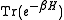
is the quantum mechanical counterpart of the canonical partition function, being the normalization factor for the mixed state of interest.
The density operator ρ obtained above therefore describes the (mixed) state of a canonical ensemble of quantum mechanical systems. As with any density operator, if A is a physical observable, then its expected value is
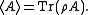
Relations with other ensembles
A generalization of this is the grand canonical ensembleGrand canonical ensemble
In statistical mechanics, a grand canonical ensemble is a theoretical collection of model systems put together to mirror the calculated probability distribution of microscopic states of a given physical system which is being maintained in a given macroscopic state...
, in which the systems may share particles as well as energy. By contrast, in the microcanonical ensemble
Microcanonical ensemble
In statistical physics, the microcanonical ensemble is a theoretical tool used to describe the thermodynamic properties of an isolated system. In such a system, the possible macrostates of the system all have the same energy and the probability for the system to be in any given microstate is the same...
, the energy of each individual system is fixed.
See also
- Partition function (mathematics)Partition function (mathematics)The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...