Partition function (mathematics)
Encyclopedia
The partition function or configuration integral, as used in probability theory
, information science
and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant
in probability theory, for the Boltzmann distribution
. The partition function occurs in many problems of probability theory because, in situations where there is a natural symmetry, its associated probability measure
, the Gibbs measure
, has the Markov property
. This means that the partition function occurs not only in physical systems with translation symmetry, but also in such varied settings as neural networks (the Hopfield network), and applications such as genomics
, corpus linguistics
and artificial intelligence
, which employ Markov network
s, and Markov logic network
s. The Gibbs measure is also the unique measure that has the property of maximizing the entropy for a fixed expectation value of the energy; this underlies the appearance of the partition function in maximum entropy methods and the algorithms derived therefrom.
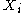taking on values 
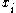, and some sort of potential function
or Hamiltonian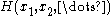
, the partition function is defined as
The function H is understood to be a real-valued function on the space of states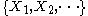
, while 
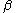is a real-valued free parameter (conventionally, the inverse temperature). The sum over the 
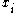is understood to be a sum over all possible values that the random variable 
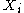may take. Thus, the sum is to be replaced by an integral
when the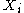
are continuous, rather than discrete. Thus, one writes
for the case of continuously-varying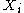
.
The number of variables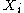
need not be countable, in which case the sums are to be replaced by functional integrals. Although there are many notations for functional integrals, a common one would be
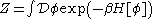
Such is the case for the partition function in quantum field theory.
A common, useful modification to the partition function is to introduce auxiliary functions. This allows, for example, the partition function to be used as a generating function
for correlation function
s. This is discussed in greater detail below.
is best understood by examining the derivation of the partition function with maximum entropy methods. Here, the parameter appears as a Lagrange multiplier; the multiplier is used to guarantee that the expectation value of some quantity is preserved by the distribution of probabilities. Thus, in physics problems, the use of just one parameter 
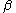reflects the fact that there is only one expectation value that must be held constant: this is the energy. For the grand canonical ensemble
, there are two Lagrange multipliers: one to hold the energy constant, and another (the fugacity
) to hold the particle count constant. In the general case, there are a set of parameters taking the place of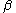
, one for each constraint enforced by the multiplier. Thus, for the general case, one has
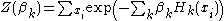
The corresponding Gibbs measure
then provides a probability distribution such that the expectation value of each
is a fixed value.
Although the value of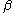
is commonly taken to be real, it need not be, in general; this is discussed in the section Normalization below.
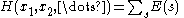
where the sum over s is a sum over some subset of the power set P(X) of the set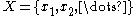
. For example, in statistical mechanics
, such as the Ising model
, the sum is over pairs of nearest neighbors. In probability theory, such as Markov networks, the sum might be over the cliques
of a graph; so, for the Ising model and other lattice models
, the maximal cliques are edges.
The fact that the potential function can be written as a sum usually reflects the fact that it is invariant under the action
of a group symmetry
, such as translational invariance. Such symmetries can be discrete or continuous; they materialize in the correlation function
s for the random variables (discussed below). Thus a symmetry in the Hamiltonian becomes a symmetry of the correlation function (and vice-versa).
This symmetry has a critically important interpretation in probability theory: it implies that the Gibbs measure
has the Markov property
; that is, it is independent of the random variables in a certain way, or, equivalently, the measure is identical on the equivalence classes of the symmetry. This leads to the widespread appearance of the partition function in problems with the Markov property, such as Hopfield networks.
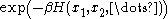
can be interpreted as a likelihood that a specific configuration
of values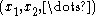
occurs in the system. Thus, given a specific configuration 
,
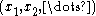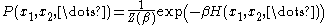
is the probability
of the configuration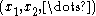
occurring in the system, which is now properly normalized so that 
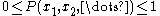, and such that the sum over all configurations totals to one. As such, the partition function can be understood to provide a measure
on the space of states
; it is sometimes called the Gibbs measure
. More narrowly, it is called the canonical ensemble
in statistical mechanics.
There exists at least one configuration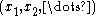
for which the probability is maximized; this configuration is conventionally called the ground state
. If the configuration is unique, the ground state is said to be non-degenerate, and the system is said to be ergodic; otherwise the ground state is degenerate. The ground state may or may not commute with the generators of the symmetry; if commutes, it is said to be an invariant measure
. When it does not commute, the symmetry is said to be spontaneously broken.
Conditions under which a ground state exists and is unique are given by the Karush–Kuhn–Tucker conditions; these conditions are commonly used to justify the use of the Gibbs measure in maximum-entropy problems.
depend on the mathematical space
over which the random field varies. Thus, real-valued random fields take values on a simplex
: this the geometrical way of saying that the sum of probabilities must total to one. For quantum mechanics, the random variables ranges over complex projective space
(or complex-valued Hilbert space
), because the random variables are interpreted as probability amplitude
s. The emphasis here is on the word projective, as the amplitudes are still normalized to one. The normalization for the potential function is the Jacobian for the appropriate mathematical space: it is 1 for ordinary probabilities, and i for complex Hilbert space; thus, in quantum field theory, one sees
in the exponential, rather than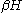 
.
for expectation values of various functions of the random variables. So, for example, taking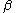
as an adjustable parameter, then the derivative of 
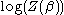with respect to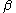 
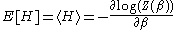
gives the average (expectation value) of H. In physics, this would be called the average energy
of the system.
The entropy is given by
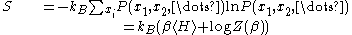
The Gibbs measure is the unique statistical distribution that maximizes the entropy for a fixed expectation value of the energy; this underlies its use in maximum entropy methods.
By introducing artificial auxiliary functions
into the partition function, it can then be used to obtain the expectation value of the random variables. Thus, for example, by writing
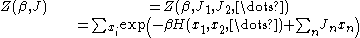
one then has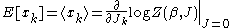
as the expectation value of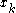
.
s of the random variables. Thus the correlation function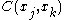
between variables 
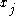and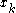 
is given by:
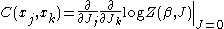
For the case where H can be written as a quadratic form
involving a differential operator
, that is, as
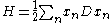
then the correlation function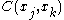
can be understood to be the Green's function
for the differential operator (and generally giving rise to Fredholm theory
).
and are subject to the renormalization group
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, information science
Information science
-Introduction:Information science is an interdisciplinary science primarily concerned with the analysis, collection, classification, manipulation, storage, retrieval and dissemination of information...
and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant
Normalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
in probability theory, for the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
. The partition function occurs in many problems of probability theory because, in situations where there is a natural symmetry, its associated probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
, the Gibbs measure
Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
, has the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
. This means that the partition function occurs not only in physical systems with translation symmetry, but also in such varied settings as neural networks (the Hopfield network), and applications such as genomics
Genomics
Genomics is a discipline in genetics concerning the study of the genomes of organisms. The field includes intensive efforts to determine the entire DNA sequence of organisms and fine-scale genetic mapping efforts. The field also includes studies of intragenomic phenomena such as heterosis,...
, corpus linguistics
Corpus linguistics
Corpus linguistics is the study of language as expressed in samples or "real world" text. This method represents a digestive approach to deriving a set of abstract rules by which a natural language is governed or else relates to another language. Originally done by hand, corpora are now largely...
and artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
, which employ Markov network
Markov network
A Markov random field, Markov network or undirected graphical model is a set of variables having a Markov property described by an undirected graph. A Markov random field is similar to a Bayesian network in its representation of dependencies...
s, and Markov logic network
Markov logic network
A Markov logic network is a probabilistic logic which applies the ideas of a Markov network to first-order logic, enabling uncertain inference...
s. The Gibbs measure is also the unique measure that has the property of maximizing the entropy for a fixed expectation value of the energy; this underlies the appearance of the partition function in maximum entropy methods and the algorithms derived therefrom.
Definition
Given a set of random variables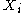 taking on values 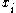, and some sort of potential functionPotential function
The term potential function may refer to:* A mathematical function whose values are a physical potential.* The class of functions known as harmonic functions, which are the topic of study in potential theory.* The potential function of a potential game....
or Hamiltonian
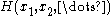, the partition function is defined asThe function H is understood to be a real-valued function on the space of states
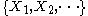, while 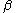is a real-valued free parameter (conventionally, the inverse temperature). The sum over the 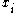is understood to be a sum over all possible values that the random variable 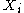may take. Thus, the sum is to be replaced by an integralIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
when the
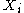are continuous, rather than discrete. Thus, one writesfor the case of continuously-varying
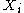.The number of variables
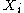need not be countable, in which case the sums are to be replaced by functional integrals. Although there are many notations for functional integrals, a common one would be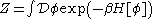Such is the case for the partition function in quantum field theory.
A common, useful modification to the partition function is to introduce auxiliary functions. This allows, for example, the partition function to be used as a generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for correlation function
Correlation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
s. This is discussed in greater detail below.
The parameter β
The role or meaning of the parameter is best understood by examining the derivation of the partition function with maximum entropy methods. Here, the parameter appears as a Lagrange multiplier; the multiplier is used to guarantee that the expectation value of some quantity is preserved by the distribution of probabilities. Thus, in physics problems, the use of just one parameter 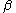reflects the fact that there is only one expectation value that must be held constant: this is the energy. For the grand canonical ensembleGrand canonical ensemble
In statistical mechanics, a grand canonical ensemble is a theoretical collection of model systems put together to mirror the calculated probability distribution of microscopic states of a given physical system which is being maintained in a given macroscopic state...
, there are two Lagrange multipliers: one to hold the energy constant, and another (the fugacity
Fugacity
In chemical thermodynamics, the fugacity of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas ...
) to hold the particle count constant. In the general case, there are a set of parameters taking the place of
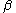, one for each constraint enforced by the multiplier. Thus, for the general case, one has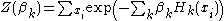The corresponding Gibbs measure
Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
then provides a probability distribution such that the expectation value of each
is a fixed value.Although the value of
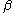is commonly taken to be real, it need not be, in general; this is discussed in the section Normalization below.Symmetry
The potential function itself commonly takes the form of a sum: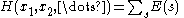where the sum over s is a sum over some subset of the power set P(X) of the set
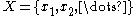. For example, in statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, such as the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
, the sum is over pairs of nearest neighbors. In probability theory, such as Markov networks, the sum might be over the cliques
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
of a graph; so, for the Ising model and other lattice models
Lattice model (physics)
In physics, a lattice model is a physical model that is defined on a lattice, as opposed to the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are...
, the maximal cliques are edges.
The fact that the potential function can be written as a sum usually reflects the fact that it is invariant under the action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of a group symmetry
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, such as translational invariance. Such symmetries can be discrete or continuous; they materialize in the correlation function
Correlation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
s for the random variables (discussed below). Thus a symmetry in the Hamiltonian becomes a symmetry of the correlation function (and vice-versa).
This symmetry has a critically important interpretation in probability theory: it implies that the Gibbs measure
Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
has the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
; that is, it is independent of the random variables in a certain way, or, equivalently, the measure is identical on the equivalence classes of the symmetry. This leads to the widespread appearance of the partition function in problems with the Markov property, such as Hopfield networks.
As a measure
The value of the expression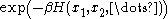can be interpreted as a likelihood that a specific configuration
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
of values
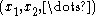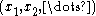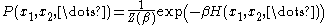
occurs in the system. Thus, given a specific configuration ,is the probability
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the configuration
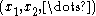occurring in the system, which is now properly normalized so that 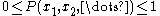, and such that the sum over all configurations totals to one. As such, the partition function can be understood to provide a measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on the space of states
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
; it is sometimes called the Gibbs measure
Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
. More narrowly, it is called the canonical ensemble
Canonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
in statistical mechanics.
There exists at least one configuration
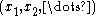for which the probability is maximized; this configuration is conventionally called the ground stateGround state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
. If the configuration is unique, the ground state is said to be non-degenerate, and the system is said to be ergodic; otherwise the ground state is degenerate. The ground state may or may not commute with the generators of the symmetry; if commutes, it is said to be an invariant measure
Invariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
. When it does not commute, the symmetry is said to be spontaneously broken.
Conditions under which a ground state exists and is unique are given by the Karush–Kuhn–Tucker conditions; these conditions are commonly used to justify the use of the Gibbs measure in maximum-entropy problems.
Normalization
The values taken by depend on the mathematical spaceMathematical space
In mathematics, a space is a set with some added structure.Mathematical spaces often form a hierarchy, i.e., one space may inherit all the characteristics of a parent space...
over which the random field varies. Thus, real-valued random fields take values on a simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
: this the geometrical way of saying that the sum of probabilities must total to one. For quantum mechanics, the random variables ranges over complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
(or complex-valued Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
), because the random variables are interpreted as probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
s. The emphasis here is on the word projective, as the amplitudes are still normalized to one. The normalization for the potential function is the Jacobian for the appropriate mathematical space: it is 1 for ordinary probabilities, and i for complex Hilbert space; thus, in quantum field theory, one sees
in the exponential, rather than 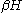.Expectation values
The partition function is commonly used as a generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for expectation values of various functions of the random variables. So, for example, taking
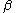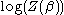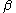
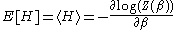
as an adjustable parameter, then the derivative of with respect to gives the average (expectation value) of H. In physics, this would be called the average energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of the system.
The entropy is given by
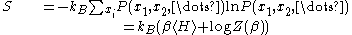
The Gibbs measure is the unique statistical distribution that maximizes the entropy for a fixed expectation value of the energy; this underlies its use in maximum entropy methods.
By introducing artificial auxiliary functions
into the partition function, it can then be used to obtain the expectation value of the random variables. Thus, for example, by writing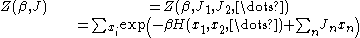one then has
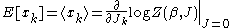
as the expectation value of
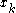.Correlation functions
Multiple differentiations lead to the correlation functionCorrelation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
s of the random variables. Thus the correlation function
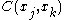between variables 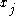and 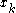is given by: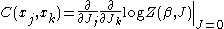For the case where H can be written as a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
involving a differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
, that is, as
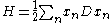
then the correlation function
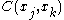can be understood to be the Green's functionGreen's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
for the differential operator (and generally giving rise to Fredholm theory
Fredholm theory
In mathematics, Fredholm theory is a theory of integral equations. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory of Fredholm...
).
General properties
Partition functions often show critical scaling, universalityUniversality (dynamical systems)
In statistical mechanics, universality is the observation that there are properties for a large class of systems that are independent of the dynamical details of the system. Systems display universality in a scaling limit, when a large number of interacting parts come together...
and are subject to the renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
.