Markov logic network
Encyclopedia
A Markov logic network is a probabilistic logic
which applies the ideas of a Markov network
to first-order logic
, enabling uncertain inference
. Markov logic networks generalize first-order logic, in the sense that, in a certain limit, all unsatisfiable statements have a probability of zero, and all tautologies
have probability one.
, the weight. Taken as a Markov network, the vertices of the network graph are atomic formula
s, and the edges are the logical connective
s used to construct the formula. Each formula is considered to be a clique
, and the Markov blanket
is the set of formulas in which a given atom appears. A potential function is associated to each formula, and takes the value of one when the formula is true, and zero when it is false. The potential function is combined with the weight to form the Gibbs measure
and partition function
for the Markov network.
The above definition glosses over a subtle point: atomic formulas do not have a truth value unless they are grounded
and given an interpretation
; that is, until they are ground atoms with a Herbrand interpretation
. Thus, a Markov logic network becomes a Markov network only with respect to a specific grounding and interpretation; the resulting Markov network is called the ground Markov network. The vertices of the graph of the ground Markov network are the ground atoms. The size of the resulting Markov network thus depends strongly (exponentially) on the number of constants in the domain of discourse
.
of the system, or one that is close to it; that this may be difficult or not always possible is illustrated by the richness of behaviour seen in the Ising model
. As in a Markov network, the stationary distribution finds the most likely assignment of probabilities to the vertices of the graph; in this case, the vertices are the ground atoms of an interpretation. That is, the distribution indicates the probability of the truth or falsehood of each ground atom. Given the stationary distribution, one can then perform inference in the traditional statistical sense of conditional probability
: obtain the probability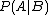
that formula A holds, given that formula B is true.
Inference in MLNs can be performed using standard Markov network inference techniques over the minimal subset of the relevant Markov network required for answering the query. These techniques include Gibbs sampling
, which is effective but may be excessively slow for large networks, belief propagation
, or approximation via pseudolikelihood
.
.
Probabilistic logic
The aim of a probabilistic logic is to combine the capacity of probability theory to handle uncertainty with the capacity of deductive logic to exploit structure. The result is a richer and more expressive formalism with a broad range of possible application areas...
which applies the ideas of a Markov network
Markov network
A Markov random field, Markov network or undirected graphical model is a set of variables having a Markov property described by an undirected graph. A Markov random field is similar to a Bayesian network in its representation of dependencies...
to first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, enabling uncertain inference
Uncertain inference
Uncertain inference was first described by Rijsbergen as a way to formally define a query and document relationship in Information retrieval. This formalization is a logical implication with an attached measure of uncertainty.-Definitions:...
. Markov logic networks generalize first-order logic, in the sense that, in a certain limit, all unsatisfiable statements have a probability of zero, and all tautologies
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
have probability one.
Description
Briefly, it is a collection of formulas from first order logic, to each of which is assigned a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, the weight. Taken as a Markov network, the vertices of the network graph are atomic formula
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
s, and the edges are the logical connective
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
s used to construct the formula. Each formula is considered to be a clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
, and the Markov blanket
Markov blanket
In machine learning, the Markov blanket for a node A in a Bayesian network is the set of nodes \partial A composed of A's parents, its children, and its children's other parents. In a Markov network, the Markov blanket of a node is its set of neighbouring nodes...
is the set of formulas in which a given atom appears. A potential function is associated to each formula, and takes the value of one when the formula is true, and zero when it is false. The potential function is combined with the weight to form the Gibbs measure
Gibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
and partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
for the Markov network.
The above definition glosses over a subtle point: atomic formulas do not have a truth value unless they are grounded
Ground expression
In mathematical logic, a ground term of a formal system is a term that does not contain any variables at all, and a closed term is a term that has no free variables...
and given an interpretation
Interpretation (logic)
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation...
; that is, until they are ground atoms with a Herbrand interpretation
Herbrand interpretation
In mathematical logic, a Herbrand interpretation is an interpretation in which all constants and function symbols are assigned very simple meanings. Specifically, every constant is interpreted as itself, and every function symbol is interpreted as the function that applies it...
. Thus, a Markov logic network becomes a Markov network only with respect to a specific grounding and interpretation; the resulting Markov network is called the ground Markov network. The vertices of the graph of the ground Markov network are the ground atoms. The size of the resulting Markov network thus depends strongly (exponentially) on the number of constants in the domain of discourse
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
.
Inference
The goal of inference in a Markov logic network is to find the stationary distributionStationary distribution
Stationary distribution may refer to:* The limiting distribution in a Markov chain* The marginal distribution of a stationary process or stationary time series* The set of joint probability distributions of a stationary process or stationary time series...
of the system, or one that is close to it; that this may be difficult or not always possible is illustrated by the richness of behaviour seen in the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
. As in a Markov network, the stationary distribution finds the most likely assignment of probabilities to the vertices of the graph; in this case, the vertices are the ground atoms of an interpretation. That is, the distribution indicates the probability of the truth or falsehood of each ground atom. Given the stationary distribution, one can then perform inference in the traditional statistical sense of conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
: obtain the probability
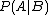that formula A holds, given that formula B is true.Inference in MLNs can be performed using standard Markov network inference techniques over the minimal subset of the relevant Markov network required for answering the query. These techniques include Gibbs sampling
Gibbs sampling
In statistics and in statistical physics, Gibbs sampling or a Gibbs sampler is an algorithm to generate a sequence of samples from the joint probability distribution of two or more random variables...
, which is effective but may be excessively slow for large networks, belief propagation
Belief propagation
Belief propagation is a message passing algorithm for performing inference on graphical models, such as Bayesian networks and Markov random fields. It calculates the marginal distribution for each unobserved node, conditional on any observed nodes...
, or approximation via pseudolikelihood
Pseudolikelihood
In statistical theory, a pseudolikelihood is an approximation to the joint probability distribution of a collection of random variables. The practical use of this is that it can provide an approximation to the likelihood function of a set of observed data which may either provide a computationally...
.
History
Markov logic networks have been studied extensively by members of the Statistical Relational Learning group at the University of WashingtonUniversity of Washington
University of Washington is a public research university, founded in 1861 in Seattle, Washington, United States. The UW is the largest university in the Northwest and the oldest public university on the West Coast. The university has three campuses, with its largest campus in the University...
.
Resources
- Matthew Richardson and Pedro Domingos, "Markov Logic Networks." Machine Learning, 62 (2006), pp 107-136.
External links
- University of Washington Statistical Relational Learning group
- Alchemy: Markov logic networks in C++
- ProbCog: Markov logic networks in Python and Java
- PyMLNs: Markov logic networks in Python (includes GUI wrappers for Alchemy)
- markov thebeast: Markov logic networks in Java
- Tuffy: A Scalable MLN Inference Engine