Enharmonic genus
Encyclopedia
The enharmonic genus has historically been the most mysterious and controversial of the three Greek genera (genres) of tetrachord
s. Its characteristic interval is a major third
, leaving the remainder of the tetrachord (the pyknon) to be divided by two intervals smaller than a semitone (approximately quarter tone
s). Because it is not easily represented by Pythagorean tuning
or meantone temperament
, there was much fascination with it in the Renaissance
. It has nothing to do with modern uses of the term enharmonic
.
above it, or a simple grave accent or downward-pointing arrow ↓. For a quarter-tone sharp, some symbols are h (half sharp), a sharp with either a downward-pointing arrow or a grave accent
above it, or a simple acute accent or upward-pointing arrow ↑. Three-quarter flat and sharp symbols are formed similarly. Other symbols are a struck-through or crossed flat (
), or a backward flat for quarter flats, and ‡ or 
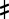for quarter sharp. Hence modern notation for an enharmonic tetrachord would be:
or
The double-flat symbol is preferred for modern notation of the third tone in the tetrachord to keep scale notes in letter sequence, and to remind the reader that the third tone in an enharmonic tetrachord (say F, shown above) was not tuned quite the same as the second note in a diatonic or chromatic scale (the E expected instead of F).
Like the diatonic scale, the ancient Greek enharmonic scale also had seven notes to the octave (assuming alternating conjunct and disjunct tetrachords), not 24 as one might imagine by analogy to the modern chromatic scale. A scale generated from two disjunct enharmonic tetrachords is:
with the corresponding conjunct tetrachords forming
Ancient Greek notation, transferred to modern notation might be more analogous to:
). Some scholars believe that the pyknon was originally undivided, resulting in a pentatonic scale similar to the Japanese iwato
. Only later was the semitone split into two microtones.
Archytas
as usual gives a tuning with small-number ratios:
hypate parhypate lichanos mese
4/3 9/7 5/4 1/1
| 28/27 |36/35| 5/4 |
-498 -435 -386 0 cents
Didymus
uses the same major third (5/4) but divides the pyknon with the arithmetic mean
of the string lengths (so therefore the harmonic mean
of the frequencies):
hypate parhypate lichanos mese
4/3 31/24 5/4 1/1
|32/31 |31/30 | 5/4 |
-498 -443 -386 0 cents
Tetrachord
Traditionally, a tetrachord is a series of three intervals filling in the interval of a perfect fourth, a 4:3 frequency proportion. In modern usage a tetrachord is any four-note segment of a scale or tone row. The term tetrachord derives from ancient Greek music theory...
s. Its characteristic interval is a major third
Major third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
, leaving the remainder of the tetrachord (the pyknon) to be divided by two intervals smaller than a semitone (approximately quarter tone
Quarter tone
A quarter tone , is a pitch halfway between the usual notes of a chromatic scale, an interval about half as wide as a semitone, which is half a whole tone....
s). Because it is not easily represented by Pythagorean tuning
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
or meantone temperament
Meantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
, there was much fascination with it in the Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
. It has nothing to do with modern uses of the term enharmonic
Enharmonic
In modern musical notation and tuning, an enharmonic equivalent is a note , interval , or key signature which is equivalent to some other note, interval, or key signature, but "spelled", or named, differently...
.
Notation
Modern notation for enharmonic notes requires two special symbols for raised and lowered quarter tones or half-semitones or quarter steps. Some symbols used for a quarter-tone flat are a flat with either an upward-pointing arrow or an acute accentAcute accent
The acute accent is a diacritic used in many modern written languages with alphabets based on the Latin, Cyrillic, and Greek scripts.-Apex:An early precursor of the acute accent was the apex, used in Latin inscriptions to mark long vowels.-Greek:...
above it, or a simple grave accent or downward-pointing arrow ↓. For a quarter-tone sharp, some symbols are h (half sharp), a sharp with either a downward-pointing arrow or a grave accent
Grave accent
The grave accent is a diacritical mark used in written Breton, Catalan, Corsican, Dutch, French, Greek , Italian, Mohawk, Norwegian, Occitan, Portuguese, Scottish Gaelic, Vietnamese, Welsh, Romansh, and other languages.-Greek:The grave accent was first used in the polytonic orthography of Ancient...
above it, or a simple acute accent or upward-pointing arrow ↑. Three-quarter flat and sharp symbols are formed similarly. Other symbols are a struck-through or crossed flat (
), or a backward flat for quarter flats, and ‡ or 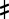for quarter sharp. Hence modern notation for an enharmonic tetrachord would be:
- D E
F G ,
or
- A B
C D .
The double-flat symbol is preferred for modern notation of the third tone in the tetrachord to keep scale notes in letter sequence, and to remind the reader that the third tone in an enharmonic tetrachord (say F, shown above) was not tuned quite the same as the second note in a diatonic or chromatic scale (the E expected instead of F).
Like the diatonic scale, the ancient Greek enharmonic scale also had seven notes to the octave (assuming alternating conjunct and disjunct tetrachords), not 24 as one might imagine by analogy to the modern chromatic scale. A scale generated from two disjunct enharmonic tetrachords is:
- D E
F G - A BC D or, in music notation starting on E: ,
with the corresponding conjunct tetrachords forming
- A B
C D EF G or, transposed to E like the previous example: .
Ancient Greek notation, transferred to modern notation might be more analogous to:
- D D 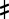D G - A A 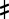A D
Tunings of the enharmonic
There is no known Pythagorean tuning of the enharmonic (the simplest recognizable enharmonic has two notes separated by a Pythagorean commaPythagorean comma
In musical tuning, the Pythagorean comma , named after the ancient mathematician and philosopher Pythagoras, is the small interval existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B , or D and C...
). Some scholars believe that the pyknon was originally undivided, resulting in a pentatonic scale similar to the Japanese iwato
Iwato
The iwato scale is a musical scale that is similar to the Locrian mode , seventh mode of the major scale, different in that it has no 3rd or 6th notes, thus making it pentatonic. It spelling is therefore 1 b2 4 b5 b7. It is used in traditional Japanese music for the koto....
. Only later was the semitone split into two microtones.
Archytas
Archytas
Archytas was an Ancient Greek philosopher, mathematician, astronomer, statesman, and strategist. He was a scientist of the Pythagorean school and famous for being the reputed founder of mathematical mechanics, as well as a good friend of Plato....
as usual gives a tuning with small-number ratios:
hypate parhypate lichanos mese
4/3 9/7 5/4 1/1
| 28/27 |36/35| 5/4 |
-498 -435 -386 0 cents
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...
Didymus
Didymus the Musician
Didymus the Musician was a music theorist in Rome of the end of the 1st century BC or beginning of the 1st century AD, who combined elements of earlier theoretical approaches with an appreciation of the aspect of performance...
uses the same major third (5/4) but divides the pyknon with the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of the string lengths (so therefore the harmonic mean
Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
of the frequencies):
hypate parhypate lichanos mese
4/3 31/24 5/4 1/1
|32/31 |31/30 | 5/4 |
-498 -443 -386 0 cents
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...
See also
- Diatonic genusDiatonic genusIn ancient Greek music theory, the diatonic genus is the division of the tetrachord from which the modern diatonic scale evolved. The distinguishing characteristic of the diatonic genus is that its largest interval is about the size of a major second...
- Chromatic genusChromatic genusIn Ancient Greek music theory, the chromatic genus is a genus of the tetrachord characterized by an upper interval of a minor third. The two middle notes of the tetrachord were movable while the two outer notes were immovable...
- Diatonic and chromaticDiatonic and chromaticDiatonic and chromatic are terms in music theory that are most often used to characterize scales, and are also applied to intervals, chords, notes, musical styles, and kinds of harmony...
- Category:Greek loanwords
- Category:Ancient Greek music
- Category:Greek music