
Pythagorean tuning
Encyclopedia
Pythagorean tuning is a system of musical tuning
in which the frequency
relationships of all intervals
are based on the ratio 3:2. This interval is chosen because it is one of the most consonant
. Its name comes from medieval texts which attribute its discovery to Pythagoras
.
The Pythagorean scale is any scale which may be constructed from only perfect fifths and octaves or the gamut of (all 12) pitches constructed from only perfect fifths and octaves and from which specific scales may be drawn.
s, each tuned in the ratio 3:2, the next simplest ratio after 2:1. Starting from D for example (D-based tuning), six other notes are produced by moving six times a ratio 3:2 up, and the remaining ones by moving the same ratio down:
This succession of eleven 3:2 intervals spans across a wide range of frequency
(on a piano keyboard, it encompasses 77 keys). Since notes differing in frequency by a factor of 2 are given the same name, it is customary to divide or multiply the frequencies of some of these notes by 2 or by a power of 2. The purpose of this adjustment is to move the 12 notes within a smaller range of frequency, namely within the interval between the base note D and the D above it (a note with twice its frequency). This interval is typically called the basic octave (on a piano keyboard, an octave
encompasses only 13 keys ).
For instance, the A is tuned such that its frequency equals 3:2 times the frequency of D — if D is tuned to a frequency of 288 Hz
, then A is tuned to 432 Hz. Similarly, the E above A is tuned such that its frequency equals 3:2 times the frequency of A, or 9:4 times the frequency of D — with A at 432 Hz, this puts E at 648 Hz. Since this E is outside the above-mentioned basic octave (i.e. its frequency is more than twice the frequency of the base note D), it is usual to halve its frequency to move it within the basic octave. Therefore, E is tuned to 324 Hz, a 9:8 above D. The B at 3:2 above that E is tuned to the ratio 27:16 and so on. Starting from the same point working the other way, G is tuned as 3:2 below D, which means that it is assigned a frequency equal to 2:3 times the frequency of D — with D at 288 Hz, this puts G at 192 Hz. This frequency is then doubled (to 384 Hz) to bring it into the basic octave.
When extending this tuning however, a problem arises: no stack of 3:2 intervals (perfect fifths) will fit exactly into any stack of 2:1 intervals (octaves). For instance a stack such as this, obtained by adding one more note to the stack shown above
will be similar but not identical in size to a stack of 7 octaves. More exactly, it will be about a quarter of a semitone
larger (see Pythagorean comma
). Thus, A and G, when brought into the basic octave, will not coincide as expected. The table below illustrates this, showing for each note in the basic octave the conventional name of the interval
from D (the base note), the formula to compute its frequency ratio, its ratio, its size in cents, and the difference (ET-dif) in cents between its size and the size of the corresponding one in the equally tempered scale.
In the formulas, the ratios 3:2 or 2:3 represent an ascending or descending perfect fifth (i.e. an increase or decrease in frequency by a perfect fifth), while 2:1 or 1:2 represent an ascending or descending octave.
The major scale
based on C, obtained from this tuning is:
In equal temperament, pairs of enharmonic
notes such as A and G are thought of as being exactly the same note — however, as the above table indicates, in Pythagorean tuning they have different ratios with respect to D, which means they are at a different frequency. This discrepancy, of about 23.46 cents, or nearly one quarter of a semitone, is known as a Pythagorean comma
.
To get around this problem, Pythagorean tuning ignores A, and uses only the 12 notes from E to G. This, as shown above, implies that only eleven just fifths are used to build the entire chromatic scale. The remaining fifth (from G to E) is left badly out-of-tune, meaning that any music which combines those two notes is unplayable in this tuning. A very out-of-tune interval such as this one is known as a wolf interval
. In the case of Pythagorean tuning, all the fifths are 701.96 cents wide, in the exact ratio 3:2, except the wolf fifth, which is only 678.49 cents wide, nearly a quarter of a semitone
flatter.
If the notes G and E need to be sounded together, the position of the wolf fifth can be changed. For example, a C-based Pithagorean tuning would produce a stack of fifths running from D to F, making F-D the wolf interval. However, there will always be one wolf fifth in Pythagorean tuning, making it impossible to play in all keys
in tune.
s, twelve intervals composed of 2 semitones, twelve intervals composed of 3 semitones, etc.).
As explained above, one of the twelve fifths (the wolf fifth) has a different size with respect to the other eleven. For a similar reason, each of the other interval types, except for the unisons and the octaves, has two different sizes in Pythagorean tuning. This is the price paid for seeking just intonation
. The tables on the right and below show their frequency ratios and their approximate sizes in cents. Interval names are given in their standard shortened form. For instance, the size of the interval from D to A, which is a perfect fifth (P5), can be found in the seventh column of the row labeled D. Strictly just (or pure) intervals are shown in bold font. Wolf interval
s are highlighted in red.
The reason why the interval sizes vary throughout the scale is that the pitches forming the scale are unevenly spaced. Namely, the frequencies defined by construction for the twelve notes determine two different semitone
s (i.e. intervals between adjacent notes):
Conversely, in an equally tempered chromatic scale, by definition the twelve pitches are equally spaced, all semitones having a size of exactly
As a consequence all intervals of any given type have the same size (e.g., all major thirds have the same size, all fifths have the same size, etc.). The price paid, in this case, is that none of them is justly tuned and perfectly consonant, except, of course, for the unison and the octave.
For a comparison with other tuning systems, see also this table.
By definition, in Pythagorean tuning 11 perfect fifths (P5 in the table) have a size of approximately 701.955 cents (700+ε cents, where ε ≈ 1.955 cents). Since the average size of the 12 fifths must equal exactly 700 cents (as in equal temperament), the other one must have a size of 700−11ε cents, which is about 678.495 cents (the wolf fifth). Notice that, as shown in the table, the latter interval, although enharmonically equivalent to a fifth, is more properly called a diminished sixth
(d6). Similarly,
In short, similar differences in width are observed for all interval types, except for unisons and octaves, and they are all multiples of ε, the difference between the Pythagorean fifth and the average fifth.
Notice that, as an obvious consequence, each augmented or diminished interval is exactly 12ε (≈ 23.460) cents narrower or wider than its enharmonic equivalent. For instance, the d6 (or wolf fifth) is 12ε cents narrower than each P5, and each A2 is 12ε cents wider than each m3. This interval of size 12ε is known as a Pythagorean comma
, exactly equal to the opposite of a diminished second
(≈ −23.460 cents). This implies that ε can be also defined as one twelfth of a Pythagorean comma.
tuned, and their frequency ratio
, shown in the table, is a superparticular number (or epimoric ratio). The same is true for the octave.
 Because of the wolf interval
Because of the wolf interval
, this tuning is rarely used nowadays, although it is thought to have been widespread. In music which does not change key
very often, or which is not very harmonically
adventurous, the wolf interval is unlikely to be a problem, as not all the possible fifths will be heard in such pieces.
Because most fifths in Pythagorean tuning are in the simple ratio of 3:2, they sound very "smooth" and consonant. The thirds, by contrast, most of which are in the relatively complex ratios of 81:64 (for major thirds) and 32:27 (for minor thirds), sound less smooth. For this reason, Pythagorean tuning is particularly well suited to music which treats fifths as consonances, and thirds as dissonances. In western classical music, this usually means music written prior to the 15th century. As thirds came to be treated as consonances, so meantone temperament
, and particularly quarter-comma meantone
, which tunes thirds to the relatively simple ratio of 5:4, became more popular. However, meantone presented its own harmonic challenges, and its wolf intervals proved to be even worse than those of the Pythagorean tuning (so much so that it often required 19 keys to the octave as opposed to the 12 in Pythagorean tuning), so it is not suitable for all music.
From around the 18th century, as the desire grew for instruments to change key, and therefore to avoid a wolf interval, this led to the widespread use of well temperament
s and eventually equal temperament
.
Musical tuning
In music, there are two common meanings for tuning:* Tuning practice, the act of tuning an instrument or voice.* Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases.-Tuning practice:...
in which the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
relationships of all intervals
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
are based on the ratio 3:2. This interval is chosen because it is one of the most consonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
. Its name comes from medieval texts which attribute its discovery to Pythagoras
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
.
The Pythagorean scale is any scale which may be constructed from only perfect fifths and octaves or the gamut of (all 12) pitches constructed from only perfect fifths and octaves and from which specific scales may be drawn.
Method
Pythagorean tuning is based on a stack of intervals called perfect fifthPerfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
s, each tuned in the ratio 3:2, the next simplest ratio after 2:1. Starting from D for example (D-based tuning), six other notes are produced by moving six times a ratio 3:2 up, and the remaining ones by moving the same ratio down:
- E♭—B♭—F—C—G—D—A—E—B—F♯—C♯—G♯
This succession of eleven 3:2 intervals spans across a wide range of frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
(on a piano keyboard, it encompasses 77 keys). Since notes differing in frequency by a factor of 2 are given the same name, it is customary to divide or multiply the frequencies of some of these notes by 2 or by a power of 2. The purpose of this adjustment is to move the 12 notes within a smaller range of frequency, namely within the interval between the base note D and the D above it (a note with twice its frequency). This interval is typically called the basic octave (on a piano keyboard, an octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
encompasses only 13 keys ).
For instance, the A is tuned such that its frequency equals 3:2 times the frequency of D — if D is tuned to a frequency of 288 Hz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
, then A is tuned to 432 Hz. Similarly, the E above A is tuned such that its frequency equals 3:2 times the frequency of A, or 9:4 times the frequency of D — with A at 432 Hz, this puts E at 648 Hz. Since this E is outside the above-mentioned basic octave (i.e. its frequency is more than twice the frequency of the base note D), it is usual to halve its frequency to move it within the basic octave. Therefore, E is tuned to 324 Hz, a 9:8 above D. The B at 3:2 above that E is tuned to the ratio 27:16 and so on. Starting from the same point working the other way, G is tuned as 3:2 below D, which means that it is assigned a frequency equal to 2:3 times the frequency of D — with D at 288 Hz, this puts G at 192 Hz. This frequency is then doubled (to 384 Hz) to bring it into the basic octave.
When extending this tuning however, a problem arises: no stack of 3:2 intervals (perfect fifths) will fit exactly into any stack of 2:1 intervals (octaves). For instance a stack such as this, obtained by adding one more note to the stack shown above
- A♭—E♭—B♭—F—C—G—D—A—E—B—F♯—C♯—G♯
will be similar but not identical in size to a stack of 7 octaves. More exactly, it will be about a quarter of a semitone
Semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
larger (see Pythagorean comma
Pythagorean comma
In musical tuning, the Pythagorean comma , named after the ancient mathematician and philosopher Pythagoras, is the small interval existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B , or D and C...
). Thus, A and G, when brought into the basic octave, will not coincide as expected. The table below illustrates this, showing for each note in the basic octave the conventional name of the interval
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
from D (the base note), the formula to compute its frequency ratio, its ratio, its size in cents, and the difference (ET-dif) in cents between its size and the size of the corresponding one in the equally tempered scale.
| Note | Interval from D | Formula | Frequency ratio |
Size (cents) |
ET-dif (cents) |
|---|---|---|---|---|---|
| A | diminished fifth | 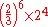 |
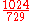 |
588.27 | -11.73 |
| E | minor second Minor second In modern Western tonal music theory a minor second is the interval between two notes on adjacent staff positions, or having adjacent note letters, whose alterations cause them to be one semitone or half-step apart, such as B and C or C and D.... |
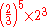 |
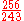 |
90.22 | −9.78 |
| B | minor sixth Minor sixth -Subminor sixth:In music, a subminor sixth or septimal sixth is an interval that is noticeably narrower than a minor sixth but noticeably wider than a diminished sixth.The sub-minor sixth is an interval of a 14:9 ratio or alternately 11:7.... |
 |
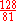 |
792.18 | −7.82 |
| F | minor third Minor third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major... |
 |
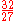 |
294.13 | −5.87 |
| C | minor seventh Minor seventh In classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the minor seventh is one of two commonly occurring sevenths. The minor quality specification identifies it as being the smallest of the two: the minor seventh spans ten semitones, the... |
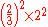 |
 |
996.09 | −3.91 |
| G | perfect fourth Perfect fourth In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there... |
 |
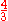 |
498.04 | -1.96 |
| D | unison Unison In music, the word unison can be applied in more than one way. In general terms, it may refer to two notes sounding the same pitch, often but not always at the same time; or to the same musical voice being sounded by several voices or instruments together, either at the same pitch or at a distance... |
 |
 |
0 .00 | 0.00 |
| A | perfect fifth Perfect fifth In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones... |
 |
 |
701.96 | 1.96 |
| E | major second Major second In Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions... |
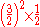 |
 |
203.91 | 3.91 |
| B | major sixth Major sixth In classical music from Western culture, a sixth is a musical interval encompassing six staff positions , and the major sixth is one of two commonly occurring sixths. It is qualified as major because it is the largest of the two... |
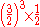 |
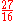 |
905.87 | 5.87 |
| F | major third Major third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three... |
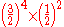 |
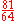 |
407.82 | 7.82 |
| C | major seventh Major seventh In classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the major seventh is one of two commonly occurring sevenths. It is qualified as major because it is the larger of the two... |
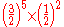 |
 |
1109.78 | 9.78 |
| G | augmented fourth |  |
 |
611.73 | 11.73 |
In the formulas, the ratios 3:2 or 2:3 represent an ascending or descending perfect fifth (i.e. an increase or decrease in frequency by a perfect fifth), while 2:1 or 1:2 represent an ascending or descending octave.
The major scale
Major scale
In music theory, the major scale or Ionian scale is one of the diatonic scales. It is made up of seven distinct notes, plus an eighth which duplicates the first an octave higher. In solfege these notes correspond to the syllables "Do, Re, Mi, Fa, Sol, La, Ti/Si, ", the "Do" in the parenthesis at...
based on C, obtained from this tuning is:
| Note | C | D | E | F | G | A | B | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 9/8 | 81/64 | 4/3 | 3/2 | 27/16 | 243/128 | 2/1 | ||||||||
| Step | — | 9/8 | 9/8 | 256/243 | 9/8 | 9/8 | 9/8 | 256/243 | — | |||||||
In equal temperament, pairs of enharmonic
Enharmonic
In modern musical notation and tuning, an enharmonic equivalent is a note , interval , or key signature which is equivalent to some other note, interval, or key signature, but "spelled", or named, differently...
notes such as A and G are thought of as being exactly the same note — however, as the above table indicates, in Pythagorean tuning they have different ratios with respect to D, which means they are at a different frequency. This discrepancy, of about 23.46 cents, or nearly one quarter of a semitone, is known as a Pythagorean comma
Pythagorean comma
In musical tuning, the Pythagorean comma , named after the ancient mathematician and philosopher Pythagoras, is the small interval existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B , or D and C...
.
To get around this problem, Pythagorean tuning ignores A, and uses only the 12 notes from E to G. This, as shown above, implies that only eleven just fifths are used to build the entire chromatic scale. The remaining fifth (from G to E) is left badly out-of-tune, meaning that any music which combines those two notes is unplayable in this tuning. A very out-of-tune interval such as this one is known as a wolf interval
Wolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
. In the case of Pythagorean tuning, all the fifths are 701.96 cents wide, in the exact ratio 3:2, except the wolf fifth, which is only 678.49 cents wide, nearly a quarter of a semitone
Semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
flatter.
If the notes G and E need to be sounded together, the position of the wolf fifth can be changed. For example, a C-based Pithagorean tuning would produce a stack of fifths running from D to F, making F-D the wolf interval. However, there will always be one wolf fifth in Pythagorean tuning, making it impossible to play in all keys
Key (music)
In music theory, the term key is used in many different and sometimes contradictory ways. A common use is to speak of music as being "in" a specific key, such as in the key of C major or in the key of F-sharp. Sometimes the terms "major" or "minor" are appended, as in the key of A minor or in the...
in tune.
Size of intervals
The table above shows only intervals from D. However, intervals can be formed by starting from each of the above listed 12 notes. Thus, twelve intervals can be defined for each interval type (twelve unisons, twelve semitoneSemitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s, twelve intervals composed of 2 semitones, twelve intervals composed of 3 semitones, etc.).
As explained above, one of the twelve fifths (the wolf fifth) has a different size with respect to the other eleven. For a similar reason, each of the other interval types, except for the unisons and the octaves, has two different sizes in Pythagorean tuning. This is the price paid for seeking just intonation
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
. The tables on the right and below show their frequency ratios and their approximate sizes in cents. Interval names are given in their standard shortened form. For instance, the size of the interval from D to A, which is a perfect fifth (P5), can be found in the seventh column of the row labeled D. Strictly just (or pure) intervals are shown in bold font. Wolf interval
Wolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
s are highlighted in red.
The reason why the interval sizes vary throughout the scale is that the pitches forming the scale are unevenly spaced. Namely, the frequencies defined by construction for the twelve notes determine two different semitone
Semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s (i.e. intervals between adjacent notes):
- The minor second (m2), also called diatonic semitone, with size
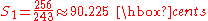
(e.g. between D and E) - The augmented unison (A1), also called chromatic semitone, with size

(e.g. between E and E)
Conversely, in an equally tempered chromatic scale, by definition the twelve pitches are equally spaced, all semitones having a size of exactly

As a consequence all intervals of any given type have the same size (e.g., all major thirds have the same size, all fifths have the same size, etc.). The price paid, in this case, is that none of them is justly tuned and perfectly consonant, except, of course, for the unison and the octave.
For a comparison with other tuning systems, see also this table.
By definition, in Pythagorean tuning 11 perfect fifths (P5 in the table) have a size of approximately 701.955 cents (700+ε cents, where ε ≈ 1.955 cents). Since the average size of the 12 fifths must equal exactly 700 cents (as in equal temperament), the other one must have a size of 700−11ε cents, which is about 678.495 cents (the wolf fifth). Notice that, as shown in the table, the latter interval, although enharmonically equivalent to a fifth, is more properly called a diminished sixth
Diminished sixth
In classical music from Western culture, a diminished sixth is an interval produced by narrowing a minor sixth by a chromatic semitone. For example, the interval from A to F is a minor sixth, eight semitones wide, and both the intervals from A to F, and from A to F are diminished sixths, spanning...
(d6). Similarly,
- 9 minor thirdMinor thirdIn classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major...
s (m3) are ≈ 294.135 cents (300−3ε), 3 augmented secondAugmented secondIn classical music from Western culture, an augmented second is an interval produced by widening a major second by a chromatic semitone. For instance, the interval from C to D is a major second, two semitones wide, and both the intervals from C to D, and from C to D are augmented seconds, spanning...
s (A2) are ≈ 317.595 cents (300+9ε), and their average is 300 cents; - 8 major thirdMajor thirdIn classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
s (M3) are ≈ 407.820 cents (400+4ε), 4 diminished fourthDiminished fourthIn classical music from Western culture, a diminished fourth is an interval produced by narrowing a perfect fourth by a chromatic semitone. For example, the interval from C to F is a perfect fourth, five semitones wide, and both the intervals from C to F, and from C to F are diminished fourths,...
s (d4) are ≈ 384.360 cents (400−8ε), and their average is 400 cents; - 7 diatonic semitoneSemitoneA semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s (m2) are ≈ 90.225 cents (100−5ε), 5 chromatic semitones (A1) are ≈ 113.685 cents (100+7ε), and their average is 100 cents.
In short, similar differences in width are observed for all interval types, except for unisons and octaves, and they are all multiples of ε, the difference between the Pythagorean fifth and the average fifth.
Notice that, as an obvious consequence, each augmented or diminished interval is exactly 12ε (≈ 23.460) cents narrower or wider than its enharmonic equivalent. For instance, the d6 (or wolf fifth) is 12ε cents narrower than each P5, and each A2 is 12ε cents wider than each m3. This interval of size 12ε is known as a Pythagorean comma
Pythagorean comma
In musical tuning, the Pythagorean comma , named after the ancient mathematician and philosopher Pythagoras, is the small interval existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B , or D and C...
, exactly equal to the opposite of a diminished second
Diminished second
In modern Western tonal music theory a diminished second is the interval between notes on two adjacent staff positions, or having adjacent note letters, whose alterations cause them, in ordinary equal temperament, to have no pitch difference, such as B and C or B and C...
(≈ −23.460 cents). This implies that ε can be also defined as one twelfth of a Pythagorean comma.
Pythagorean intervals
Four of the above mentioned intervals take a specific name in Pythagorean tuning. In the following table, these specific names are provided, together with alternative names used generically for some other intervals. Notice that the Pythagorean comma does not coincide with the diminished second, as its size (524288:531441) is the reciprocal of the Pythagorean diminished second (531441:524288). Also ditone and semiditone are specific for Pythagorean tuning, while tone and tritone are used generically for all tuning systems. Interestingly, despite its name, a semiditone (3 semitones, or about 300 cents) can hardly be viewed as half of a ditone (4 semitones, or about 400 cents). All the intervals with prefix sesqui- are justlyJust intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
tuned, and their frequency ratio
Interval ratio
In music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth is 3:2 , 1.5, and may be approximated by an equal tempered perfect fifth which is 27/12, 1.498...
, shown in the table, is a superparticular number (or epimoric ratio). The same is true for the octave.
| Number of semitones | |Specific names | ||||||
|---|---|---|---|---|---|---|---|
| Quality and number | |Pythagorean tuning | |1/4-comma meantone |
|||||
| Full | Short | ||||||
| 0 | comma Comma A comma is a type of punctuation mark . The word comes from the Greek komma , which means something cut off or a short clause.Comma may also refer to:* Comma , a type of interval in music theory... |
Pythagorean comma Pythagorean comma In musical tuning, the Pythagorean comma , named after the ancient mathematician and philosopher Pythagoras, is the small interval existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B , or D and C... (524288:531441) |
diesis Diesis In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents... (128:125) |
||||
| 0 | diminished second Diminished second In modern Western tonal music theory a diminished second is the interval between notes on two adjacent staff positions, or having adjacent note letters, whose alterations cause them, in ordinary equal temperament, to have no pitch difference, such as B and C or B and C... |
d2 | (531441:524288) | ||||
| 1 | minor second Minor second In modern Western tonal music theory a minor second is the interval between two notes on adjacent staff positions, or having adjacent note letters, whose alterations cause them to be one semitone or half-step apart, such as B and C or C and D.... |
m2 | semitone, half tone, half step |
diatonic semitone, minor semitone |
limma (256:243) | ||
| 1 | augmented unison Augmented unison In modern Western tonal music theory an augmented unison is the interval between two notes on the same staff position, or having the same note letter, whose alterations cause them, in ordinary equal temperament, to be one semitone apart. In other words, it is a unison where one note has been raised... |
A1 | chromatic semitone, major semitone |
apotome (2187:2048) | |||
| 2 | diminished third Diminished third In classical music from Western culture, a diminished third is the musical interval produced by narrowing a minor third by a chromatic semitone. For instance, the interval from A to C is a minor third, three semitones wide, and both the intervals from A to C, and from A to C are diminished thirds,... |
d3 | tone, whole tone, whole step | ||||
| 2 | major second Major second In Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions... |
M2 | sesquioctavum (9:8) | ||||
| 3 | minor third Minor third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major... |
m3 | semiditone (32:27) | sesquiquintum (6:5) | |||
| 4 | major third Major third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three... |
M3 | ditone Ditone In music, a ditone is the interval 81:64, which is 407.82 cents. It is the major third in Pythagorean tuning. The ditone is evenly divisible by two major tones and is wider than a just major third by a syntonic comma... (81:64) |
sesquiquartum (5:4) | |||
| 5 | perfect fourth Perfect fourth In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there... |
P4 | diatessaron | sesquitertium (4:3) | |||
| 6 | diminished fifth | d5 | tritone | ||||
| 6 | augmented fourth | A4 | |||||
| 7 | perfect fifth Perfect fifth In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones... |
P5 | diapente | sesquialterum (3:2) | |||
| 12 | (perfect) octave Octave In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"... |
P8 | diapason | duplex (2:1) | |||
History

Wolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
, this tuning is rarely used nowadays, although it is thought to have been widespread. In music which does not change key
Key (music)
In music theory, the term key is used in many different and sometimes contradictory ways. A common use is to speak of music as being "in" a specific key, such as in the key of C major or in the key of F-sharp. Sometimes the terms "major" or "minor" are appended, as in the key of A minor or in the...
very often, or which is not very harmonically
Harmony
In music, harmony is the use of simultaneous pitches , or chords. The study of harmony involves chords and their construction and chord progressions and the principles of connection that govern them. Harmony is often said to refer to the "vertical" aspect of music, as distinguished from melodic...
adventurous, the wolf interval is unlikely to be a problem, as not all the possible fifths will be heard in such pieces.
Because most fifths in Pythagorean tuning are in the simple ratio of 3:2, they sound very "smooth" and consonant. The thirds, by contrast, most of which are in the relatively complex ratios of 81:64 (for major thirds) and 32:27 (for minor thirds), sound less smooth. For this reason, Pythagorean tuning is particularly well suited to music which treats fifths as consonances, and thirds as dissonances. In western classical music, this usually means music written prior to the 15th century. As thirds came to be treated as consonances, so meantone temperament
Meantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
, and particularly quarter-comma meantone
Quarter-comma meantone
Quarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning...
, which tunes thirds to the relatively simple ratio of 5:4, became more popular. However, meantone presented its own harmonic challenges, and its wolf intervals proved to be even worse than those of the Pythagorean tuning (so much so that it often required 19 keys to the octave as opposed to the 12 in Pythagorean tuning), so it is not suitable for all music.
From around the 18th century, as the desire grew for instruments to change key, and therefore to avoid a wolf interval, this led to the widespread use of well temperament
Well temperament
Well temperament is a type of tempered tuning described in 20th-century music theory. The term is modelled on the German word wohltemperiert which appears in the title of J.S. Bach's famous composition, The Well-Tempered Clavier...
s and eventually equal temperament
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
.
Discography
- Gothic VoicesGothic VoicesGothic Voices is a United Kingdom based vocal ensemble specialising in repertoire from the 11th to the 15th century. The group was formed in 1981 by scholar and musician Christopher Page....
– Music for the Lion-Hearted King (Hyperion, CDA66336, 1989), directed by Christopher PageChristopher PageChristopher Page is an expert on medieval music, instruments and performance practice. He has written seven books regarding medieval music...
(Leech-Wilkinson) - Lou HarrisonLou HarrisonLou Silver Harrison was an American composer. He was a student of Henry Cowell, Arnold Schoenberg, and K. P. H. Notoprojo Lou Silver Harrison (May 14, 1917 – February 2, 2003) was an American composer. He was a student of Henry Cowell, Arnold Schoenberg, and K. P. H. Notoprojo Lou Silver Harrison...
performed by John SchneiderJohn Schneider (guitarist)John Schneider is a classical guitarist. He performs in just intonation and well-temperament, including pythagorean tuning, including works by Lou Harrison, LaMonte Young, John Cage, and Harry Partch...
and the Cal Arts Percussion Ensemble conducted by John BergamoJohn BergamoJohn Bergamo is an American percussionist and composer. Since 1970 he has been the coordinator of the percussion department at the California Institute of the Arts....
- Guitar & Percussion (Etceter Records, KTC1071, 1990): Suite No. 1 for guitar and percussion and Plaint & Variations on "Song of Palestine"
See also
- Enharmonic scaleEnharmonic scaleIn music theory, is, at its simplest, "a chromatic scale with each tone written in manifold notation". Relatedly, the enharmonic scale is, "an [imaginary] gradual progression by quarter tones," or any, "[musical] scale proceeding by quarter tones". More properly dieses or 'divisions', nonexistent...
- List of meantone intervals
- List of musical intervals
- Regular temperamentRegular temperamentRegular temperament is any tempered system of musical tuning such that each frequency ratio is obtainable as a product of powers of a finite number of generators, or generating frequency ratios...
- Shí-èr-lǜ
- Temperament
- Timaeus (dialogue)Timaeus (dialogue)Timaeus is one of Plato's dialogues, mostly in the form of a long monologue given by the title character, written circa 360 BC. The work puts forward speculation on the nature of the physical world and human beings. It is followed by the dialogue Critias.Speakers of the dialogue are Socrates,...
, in which Plato discusses Pythagorean tuning - Whole-tone scale
Notations
- Daniel Leech-WilkinsonDaniel Leech-WilkinsonDaniel Leech-Wilkinson is a musicologist, who is currently a Professor of Music at King's College London.He studied composition, harpsichord and the organ at the Royal College of Music, and then completed an MMus at King's College London specialising in 15th-century music...
(1997), "The good, the bad and the boring", Companion to Medieval & Renaissance Music. Oxford University Press. ISBN 0-19-816540-4.
External links
- "A Pythagorean tuning of the diatonic scale", with audio samples.
- "Pythagorean Tuning and Medieval Polyphony", by Margo Schulter.

