
Just intonation
Encyclopedia
In music, just intonation (sometimes abbreviated as JI) is any musical tuning
in which the frequencies
of note
s are related by ratio
s of small
whole numbers
. Any interval
tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series
. Frequency ratios involving large integers such as 1024:927 are not generally said to be justly tuned.
Just intonation can be contrasted and compared with equal temperament
, which dominates Western instruments of fixed pitch and default MIDI tuning. In equal temperament, all notes are defined as multiples of the same basic interval. Two notes separated by the same number of steps always have exactly the same frequency ratio. However, except for doubled frequencies (octaves), no other intervals are exact ratios of integers. Each just interval differs a different amount from its nearest equally tempered interval.
Justly tuned intervals can be written as either ratios, with a colon (for example, 3:2), or as fractions
, with a solidus
(3 ⁄ 2). For example, two tones, one at 300 Hertz
(cycles per second), and the other at 200 hertz are both multiples of 100 Hz and as such members of the harmonic series built on 100 Hz.
An A-major scale, followed by three major triads, and then a progression of fifths in equal temperament. If you listen to the above file, and then listen to this one, you might be able to hear a slight buzzing in this file.
A pair of major thirds, followed by a pair of full major chords. The first in each pair is in equal temperament; the second is in just intonation. Piano sound.
A pair of major chords. The first is in equal temperament; the second is in just intonation. The pair of chords is repeated with a transition from equal temperament to just temperament between the two chords. In the equal temperament chords a roughness or beating
can be heard at about 4 hz
and about 0.8 Hz. In the just intonation triad this roughness is absent. The square waveform makes the difference between equal and just temperaments more obvious.
, perhaps the first tuning system to be theorized in the West, is a system in which all tones can be found using powers of the ratio 3:2, an interval known as a perfect fifth
. It is easier to think of this system as a cycle of fifth
s. Because a series of 12 fifths with ratio 3:2 does not reach the same tone it began with, this system uses a wolf fifth
at the end of the cycle, to obtain its closure.
Quarter-comma meantone
obtained a more consonant tuning of the thirds
, but when limited to twelve keys (see split keys), the system does not close, leaving a very dissonant diminished sixth between the first and last tones of the cycle of fifths.
In Pythagorean tuning, the only highly consonant intervals were the perfect fifth
and its inversion, the perfect fourth
. The Pythagorean major third
(81:64) and minor third
(32:27) were dissonant
, and this prevented musicians from using triad
s and chord
s, forcing them for centuries to write music with relatively simple texture
. In late Middle Ages
, musicians realized that by slightly tempering the pitch of some notes, the Pythagorean thirds could be made consonant
. For instance, if you decrease by a syntonic comma
(81:80) the frequency of E, C-E (a major third), and E-G (a minor third) become just. Namely, C-E is flattened to a justly intonated ratio of

and at the same time E-G is sharpened to the just ratio of

The drawback is that the fifths A-E and E-B, by flattening E, become almost as dissonant as the Pythagorean wolf fifth
. But the fifth C-G stays consonant, since only E has been flattened (C-E * E-G = 5/4 * 6/5 = 3/2), and can be used together with C-E to produce a C-major
triad (C-E-G).
By generalizing this simple rationale, Gioseffo Zarlino
, in the late sixteenth century, created the first justly intonated 7-tone (diatonic
) scale, which contained pure perfect fifths (3:2), pure major thirds, and pure minor thirds:
F → A → C → E → G → B → D
This is a sequence of just major thirds (M3, ratio 5:4) and just minor thirds (m3, ratio 6:5), starting from F:
F + M3 + m3 + M3 + m3 + M3 + m3
Since M3 + m3 = P5 (perfect fifth), i.e. 5/4 * 6/5 = 3/2, this is exactly equivalent to the diatonic scale obtained in 5-limit just intonation.
The Guqin
has a musical scale based on harmonic
overtone
positions. The dots on its soundboard indicate the harmonic positions: 1/8, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 7/8.
groups that depend on close harmonies, such as barbershop quartets, usually use just intonation by design. Bagpipes
, tuned correctly, also use just intonation. There are several conventionally used instruments which, while not associated specifically with just intonation, can handle it quite well, including the trombone
and the violin family
of instruments.
or chromatic scale
in just intonation in many ways, all of which make certain chords purely tuned and as consonant and stable as possible, and the other chords not accommodated and considerably less stable.
The prominent notes of a given scale are tuned so that their frequencies form ratios of relatively small integers. For example, in the key of G major
, the ratio of the frequencies of the notes G to D (a perfect fifth
) is 3/2, while that of G to C (a perfect fourth
) is 4/3. Three basic intervals can be used to construct any interval involving the prime numbers 2, 3, and 5 (known as 5-limit just intonation):
which combine to form:
A just diatonic scale may be derived as follows. Suppose we insist that the chords F-A-C, C-E-G, and G-B-D be just major triads
(then A-C-E and E-G-B are just minor triads
, but D-F-A is not).
Then we obtain this scale:
The major thirds are correct, and two minor thirds are right, but D-F is a 32:27 semiditone. Others approaches are possible (see Five-limit tuning
), but it is impossible to get all six above-mentioned chords correct. Concerning triads, the triads on I, IV, and V are 4:5:6, the triad on ii is 27:32:40, the triads on iii and vi are 10:12:15, and the triad on vii is 45:54:64.
, can produce a twelve tone scale, but it does so by involving ratios of very large numbers, corresponding to natural harmonics very high in the harmonic series that do not occur widely in physical phenomena. This tuning uses ratios involving only powers of 3 and 2, creating a sequence of just fifths
or fourth
s, as follows:
The ratios are computed with respect to C (the base note). Starting from C, they are obtained by moving six steps to the left and six to the right. Each step consists of a multiplication of the previous pitch by 2/3 (descending fifth), 3/2 (ascending fifth), or their inversions
(3/4 or 4/3).
Between the enharmonic
notes at both ends of this sequence, is a difference in pitch
of about 24 cents
, known as the Pythagorean comma
, much closer to the unison
(0 cents) than to the semitone
(100 cents). Thus, the two notes sound almost identical. To produce a twelve tone scale, one of them is arbitrarily discarded. The twelve remaining notes are repeated by increasing or decreasing their frequencies by a multiple of 2 (the size of one or more octave
s) to build scales with multiple octaves (such as the keyboard of a piano). A drawback of Pythagorean tuning is that one of the twelve fifths in this scale is badly tuned and hence unusable (the wolf fifth, either F-D if G is discarded, or B-G if F is discarded). This twelve tone scale is fairly close to equal temperament
, but it does not offer much advantage for tonal
harmony because only the perfect intervals (fourth, fifth, and octave) are simple enough to sound pure. Major thirds, for instance, receive the rather unstable interval of 81/64, sharp of the preferred 5/4 by an 81/80 ratio. The primary reason for its use is that it is extremely easy to tune, as its building block, the perfect fifth, is the simplest and consequently the most consonant
interval after the octave and unison.
Pythagorean tuning may be regarded as a "3-limit" tuning system, because the ratios are obtained by using only powers of n, where n is at most 3.
tuning system uses a similar sequence of fifths to produce a twelve tone scale. However, it flattens the fifths by about 5.38 cents with respect to their just intonation, in order to generate justly tuned major thirds (with interval ratio 5:4).
Although this tuning system is based on a just ratio (5:4), it cannot be considered a just intonation system, because most of its intervals are irrational numbers (i.e. they cannot be expressed as fractions of integers). For instance:
To build such a twelve tone scale, we may start by constructing a table containing fifteen pitches:
The factors listed in the first row and column are powers of 3 and 5, respectively (e.g., 1/9 = 3−2). Colors indicate couples of enharmonic
notes with almost identical pitch. The ratios are all expressed relative to C in the centre of this diagram (the base note for this scale). They are computed in two steps:
Note that the powers of 2 used in the second step may be interpreted as ascending or descending octave
s. For instance, multiplying the frequency of a note by 25 means increasing it by 5 octaves. Moreover, each row of the table may be considered to be a sequence of fifths (ascending to the right), and each column a sequence of major thirds (ascending upward). For instance, in the first row of the table, there is an ascending fifth from D and A, and another one (followed by a descending octave) from A to E. This suggests an alternative but equivalent method for computing the same ratios. For instance, you can obtain A, starting from C, by moving one cell to the left and one upward in the table, which means descending by a fifth and ascending by a major third:

Since this is below C, you need to move up by an octave to end up within the desired range of ratios (from 1/1 to 2/1):

A 12 tone scale is obtained by removing one note for each couple of enharmonic notes. This can be done in at least three ways, which have in common the removal of G, according to a convention which was valid even for C-based Pythagorean and 1/4-comma meantone scales. We show here only one of the possible strategies (the others are discussed in 5-limit tuning). It consists of discarding the first column of the table (labeled "1/9"). The resulting 12-tone scale is shown below:
for further details).
, the just diatonic scale described above is used, though there are different possibilities, for instance for the 6th pitch (Dha), and further modifications may be made to all pitches excepting Sa and Pa.
Some accounts of Indian intonation system cite a given 22 Śrutis. According to some musicians, you have a scale of a given 12 pitches and ten in addition (the tonic, Shadja (Sa), and the pure fifth, Pancham (Pa), are inviolate):
Where we have two ratios for a given letter name, we have a difference of 81:80 (or 22 cents), which is known as the syntonic comma
. You can see the symmetry, looking at it from the tonic, then the octave.
(This is just one example of "explaining" a 22-Śruti scale of tones. There are many different explanations.)
s. The above scale allows a minor tone to occur next to a semitone which produces the awkward ratio 32:27 for F:D, and still worse, a minor tone next to a fourth giving 40:27 for A:D. Moving D down to 10/9 alleviates these difficulties but creates new ones: G:D becomes 27:20, and B:G becomes 27:16.
You can have more fret
s on a guitar
to handle both A's, 9/8 with respect to G and 10/9 with respect to G so that C:A can be played as 6:5 while D:A can still be played as 3:2. 9/8 and 10/9 are less than 1/53 octave apart, so mechanical and performance considerations have made this approach extremely rare. And the problem of how to tune chords such as C-E-G-A-D is left unresolved (for instance, A could be 4:3 below D (making it 9/8, if G is 1) or 4:3 above E (making it 10/9, if G is 1) but not both at the same time, so one of the fourths in the chord will have to be an out-of-tune wolf interval). However the frets may be removed entirely—this, unfortunately, makes in-tune fingering of many chords exceedingly difficult, due to the construction and mechanics of the human hand—and the tuning of most complex chords in just intonation is generally ambiguous.
Some composers deliberately use these wolf intervals and other dissonant intervals as a way to expand the tone color palette of a piece of music. For example, the extended piano pieces "The Well-Tuned Piano" by LaMonte Young, and "The Harp Of New Albion" by Terry Riley use a combination of very consonant and dissonant intervals for musical effect. In "Revelation," Michael Harrison goes even farther, and uses the tempo of beat patterns produced by some dissonant intervals as an integral part of several movements.
For many instruments tuned in just intonation, you can't change keys
without retuning your instrument. For instance, if you tune a piano to just intonation intervals and a minimum of wolf intervals for the key of G, then only one other key (typically E-flat) can have the same intervals, and many of the keys have a very dissonant and unpleasant sound. This makes modulation
within a piece, or playing a repertoire of pieces in different keys, impractical to impossible.
Synthesizer
s have proven a valuable tool for composers wanting to experiment with just intonation. Many commercial synthesizers provide the ability to use built-in just intonation scales or to program your own. Wendy Carlos
used a system on her 1986 album Beauty in the Beast
, where one electronic keyboard was used to play the notes, and another used to instantly set the root note to which all intervals were tuned, which allowed for modulation. On her 1987 lecture album Secrets of Synthesis there are audible examples of the difference in sound between equal temperament and just intonation.
ensembles naturally tend toward just intonation because of the comfort of its stability. Barbershop quartets
are a good example of this.
would be used. However, a few have specified just intonation systems for some or all of their compositions, including John Adams
, Glenn Branca
, Martin Bresnick
, Wendy Carlos
, Lawrence Chandler
, Tony Conrad
, Stuart Dempster
, David B. Doty
, Arnold Dreyblatt
, Kyle Gann
, Kraig Grady
, Lou Harrison
, Ben Johnston, Elodie Lauten
, György Ligeti
, Douglas Leedy
, Pauline Oliveros
, Harry Partch
, Robert Rich
, Terry Riley
, Marc Sabat
, Wolfgang von Schweinitz
, Adam Silverman
, James Tenney
, Daniel James Wolf
, and La Monte Young
. Eivind Groven
is often considered a just intonation composer but just intonation purists will disagree. His tuning system was in fact schismatic temperament
, which is indeed capable of far closer approximations to just intonation consonances than 12-note equal temperament or even meantone temperament
, but still alters the pure ratios of just intonation slightly in order to achieve a simpler and more flexible system than true just intonation.
Music written in just intonation is most often tonal
but need not be; some music of Kraig Grady and Daniel James Wolf uses just intonation scales designed by Erv Wilson
explicitly for a consonant
form of atonality
, and Ben Johnston's Sonata for Microtonal Piano
(1964) uses serialism
to achieve an atonal result. Composers often impose a limit
on how complex the ratios used are: for example, a composer may write in "7-limit JI", meaning that no prime number
larger than 7 features in the ratios they use. Under this scheme, the ratio 10/7, for example, would be permitted, but 11/7 would not be, as all non-prime numbers are octave
s of, or mathematically and tonally related to, lower primes (example: 12 is a double octave of 3, while 9 is a square of 3). Yuri Landman
derived a just intoned musical scale from a initially considered atonal prepared guitar
playing technique
based on adding a third bridge
under the strings. When this bridge is positioned in the noded
positions of the harmonic series
the volume of the instrument increases and the overtone
becomes clear and has a consonant relation to the complementary opposed string part creating a harmonic multiphonic
tone.
, amongst others, preferred to combine JI ratios with cents
deviations from the equal tempered pitches, indicated in a legend or directly in the score, allowing performers to readily use electronic tuning devices if desired. Beginning in the 1960s, Ben Johnston had proposed an alternative approach, redefining the understanding of conventional symbols (the seven "white" notes, the sharps and flats) and adding further accidentals, each designed to extend the notation into higher prime limits. Johnston‘s method is based on a diatonic C Major scale tuned in JI, in which the interval between D (9/8 above C) and A (5/3 above C) is one Syntonic comma
less than a Pythagorean perfect fifth 3:2. To write a perfect fifth, Johnston introduces a pair of symbols representing this comma, + and -. Thus, a series of perfect fifths beginning with F would proceed C G D A+ E+ B+. The three conventional white notes A E B are tuned as Ptolemaic major thirds (5:4) above F C G respectively. Johnston introduces new symbols for the septimal, undecimal, tridecimal, and further prime extensions to create an accidental based exact JI notation for what he has named "Extended Just Intonation".
In the years 2000-2004, Marc Sabat
and Wolfgang von Schweinitz
worked together in Berlin to develop a different accidental based method, the Extended Helmholtz-Ellis JI Pitch Notation. Following the method of notation suggested by Helmholtz in his classic "On the Sensations of Tone as a Physiological Basis for the Theory of Music", incorporating Ellis' invention of cents, and following Johnston's step into "Extended JI", Sabat and Schweinitz consider each prime dimension of harmonic space to be represented by a unique symbol. In particular they take the conventional flats, naturals and sharps as a Pythagorean series of perfect fifths. Thus, a series of perfect fifths beginning with F proceeds C G D A E B F# and so on. The advantage for musicians is that conventional reading of the basic fourths and fifths remains familiar. Such an approach has also been advocated by Daniel James Wolf
. In the Sabat-Schweinitz design, Syntonic Commas are marked by arrows attached to the flat, natural or sharp sign, Septimal Commas using Giuseppe Tartini's symbol, and Undecimal Quartertones using the common practice quartertone signs (a single cross and backwards flat). For higher primes, additional signs have been designed. To facilitate quick estimation of pitches, cents indications may be added (downward deviations below and upward deviations above the respective accidental). The convention used is that the cents written refer to the tempered pitch implied by the flat, natural, or sharp sign and the note name. One of the great advantages of such a notation is that it allows the natural harmonic series to be precisely notated. A complete legend and fonts for the notation (see samples) are open source and available from PLAINSOUND MUSIC EDITION.
Musical tuning
In music, there are two common meanings for tuning:* Tuning practice, the act of tuning an instrument or voice.* Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases.-Tuning practice:...
in which the frequencies
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
of note
Note
In music, the term note has two primary meanings:#A sign used in musical notation to represent the relative duration and pitch of a sound;#A pitched sound itself....
s are related by ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
s of small
Limit (music)
In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name...
whole numbers
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
. Any interval
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series
Harmonic series (music)
Pitched musical instruments are often based on an approximate harmonic oscillator such as a string or a column of air, which oscillates at numerous frequencies simultaneously. At these resonant frequencies, waves travel in both directions along the string or air column, reinforcing and canceling...
. Frequency ratios involving large integers such as 1024:927 are not generally said to be justly tuned.
Just intonation can be contrasted and compared with equal temperament
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
, which dominates Western instruments of fixed pitch and default MIDI tuning. In equal temperament, all notes are defined as multiples of the same basic interval. Two notes separated by the same number of steps always have exactly the same frequency ratio. However, except for doubled frequencies (octaves), no other intervals are exact ratios of integers. Each just interval differs a different amount from its nearest equally tempered interval.
Justly tuned intervals can be written as either ratios, with a colon (for example, 3:2), or as fractions
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
, with a solidus
Solidus (punctuation)
The solidus is a punctuation mark used to indicate fractions including fractional currency. It may also be called a shilling mark, an in-line fraction bar, or a fraction slash....
(3 ⁄ 2). For example, two tones, one at 300 Hertz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
(cycles per second), and the other at 200 hertz are both multiples of 100 Hz and as such members of the harmonic series built on 100 Hz.
Examples
An A-major scale, followed by three major triads, and then a progression of fifths in just intonation.An A-major scale, followed by three major triads, and then a progression of fifths in equal temperament. If you listen to the above file, and then listen to this one, you might be able to hear a slight buzzing in this file.
A pair of major thirds, followed by a pair of full major chords. The first in each pair is in equal temperament; the second is in just intonation. Piano sound.
A pair of major chords. The first is in equal temperament; the second is in just intonation. The pair of chords is repeated with a transition from equal temperament to just temperament between the two chords. In the equal temperament chords a roughness or beating
Beat (acoustics)
In acoustics, a beat is an interference between two sounds of slightly different frequencies, perceived as periodic variations in volume whose rate is the difference between the two frequencies....
can be heard at about 4 hz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
and about 0.8 Hz. In the just intonation triad this roughness is absent. The square waveform makes the difference between equal and just temperaments more obvious.
History

Recorded history
Pythagorean tuningPythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
, perhaps the first tuning system to be theorized in the West, is a system in which all tones can be found using powers of the ratio 3:2, an interval known as a perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
. It is easier to think of this system as a cycle of fifth
Circle of fifths
In music theory, the circle of fifths shows the relationships among the 12 tones of the chromatic scale, their corresponding key signatures, and the associated major and minor keys...
s. Because a series of 12 fifths with ratio 3:2 does not reach the same tone it began with, this system uses a wolf fifth
Wolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
at the end of the cycle, to obtain its closure.
Quarter-comma meantone
Quarter-comma meantone
Quarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning...
obtained a more consonant tuning of the thirds
Third (music)
In music and music theory third may refer to:*major third*minor third*augmented third/perfect fourth*diminished third/major second*Third , chord member a third above the root*Mediant, third degree of the diatonic scale...
, but when limited to twelve keys (see split keys), the system does not close, leaving a very dissonant diminished sixth between the first and last tones of the cycle of fifths.
In Pythagorean tuning, the only highly consonant intervals were the perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
and its inversion, the perfect fourth
Perfect fourth
In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
. The Pythagorean major third
Major third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
(81:64) and minor third
Minor third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major...
(32:27) were dissonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
, and this prevented musicians from using triad
Triad (music)
In music and music theory, a triad is a three-note chord that can be stacked in thirds. Its members, when actually stacked in thirds, from lowest pitched tone to highest, are called:* the Root...
s and chord
Chord (music)
A chord in music is any harmonic set of two–three or more notes that is heard as if sounding simultaneously. These need not actually be played together: arpeggios and broken chords may for many practical and theoretical purposes be understood as chords...
s, forcing them for centuries to write music with relatively simple texture
Texture (music)
In music, texture is the way the melodic, rhythmic, and harmonic materials are combined in a composition , thus determining the overall quality of sound of a piece...
. In late Middle Ages
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
, musicians realized that by slightly tempering the pitch of some notes, the Pythagorean thirds could be made consonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
. For instance, if you decrease by a syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
(81:80) the frequency of E, C-E (a major third), and E-G (a minor third) become just. Namely, C-E is flattened to a justly intonated ratio of

and at the same time E-G is sharpened to the just ratio of

The drawback is that the fifths A-E and E-B, by flattening E, become almost as dissonant as the Pythagorean wolf fifth
Wolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
. But the fifth C-G stays consonant, since only E has been flattened (C-E * E-G = 5/4 * 6/5 = 3/2), and can be used together with C-E to produce a C-major
Major chord
In music theory, a major chord is a chord having a root, a major third, and a perfect fifth. When a chord has these three notes alone, it is called a major triad...
triad (C-E-G).
By generalizing this simple rationale, Gioseffo Zarlino
Gioseffo Zarlino
Gioseffo Zarlino was an Italian music theorist and composer of the Renaissance. He was possibly the most famous music theorist between Aristoxenus and Rameau, and made a large contribution to the theory of counterpoint as well as to musical tuning.-Life:Zarlino was born in Chioggia, near Venice...
, in the late sixteenth century, created the first justly intonated 7-tone (diatonic
Diatonic scale
In music theory, a diatonic scale is a seven note, octave-repeating musical scale comprising five whole steps and two half steps for each octave, in which the two half steps are separated from each other by either two or three whole steps...
) scale, which contained pure perfect fifths (3:2), pure major thirds, and pure minor thirds:
F → A → C → E → G → B → D
This is a sequence of just major thirds (M3, ratio 5:4) and just minor thirds (m3, ratio 6:5), starting from F:
F + M3 + m3 + M3 + m3 + M3 + m3
Since M3 + m3 = P5 (perfect fifth), i.e. 5/4 * 6/5 = 3/2, this is exactly equivalent to the diatonic scale obtained in 5-limit just intonation.
The Guqin
Guqin
The guqin is the modern name for a plucked seven-string Chinese musical instrument of the zither family...
has a musical scale based on harmonic
Harmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
overtone
Overtone
An overtone is any frequency higher than the fundamental frequency of a sound. The fundamental and the overtones together are called partials. Harmonics are partials whose frequencies are whole number multiples of the fundamental These overlapping terms are variously used when discussing the...
positions. The dots on its soundboard indicate the harmonic positions: 1/8, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 7/8.
Modern practice
Today, despite the dominance of repertoire composed under equal-tempered systems and the prominence of the piano in musical training, musicians often approach just intonation either by accident or design because it is much easier to find (and hear) a point of stability than a point of calculated instability. A cappellaA cappella
A cappella music is specifically solo or group singing without instrumental sound, or a piece intended to be performed in this way. It is the opposite of cantata, which is accompanied singing. A cappella was originally intended to differentiate between Renaissance polyphony and Baroque concertato...
groups that depend on close harmonies, such as barbershop quartets, usually use just intonation by design. Bagpipes
Bagpipes
Bagpipes are a class of musical instrument, aerophones, using enclosed reeds fed from a constant reservoir of air in the form of a bag. Though the Scottish Great Highland Bagpipe and Irish uilleann pipes have the greatest international visibility, bagpipes of many different types come from...
, tuned correctly, also use just intonation. There are several conventionally used instruments which, while not associated specifically with just intonation, can handle it quite well, including the trombone
Trombone
The trombone is a musical instrument in the brass family. Like all brass instruments, sound is produced when the player’s vibrating lips cause the air column inside the instrument to vibrate...
and the violin family
Violin family
The violin family of musical instruments was developed in Italy in the sixteenth century. The standard modern violin family consists of the violin, viola, cello, and double bass....
of instruments.
Diatonic scale
It is possible to tune the familiar diatonic scaleDiatonic scale
In music theory, a diatonic scale is a seven note, octave-repeating musical scale comprising five whole steps and two half steps for each octave, in which the two half steps are separated from each other by either two or three whole steps...
or chromatic scale
Chromatic scale
The chromatic scale is a musical scale with twelve pitches, each a semitone apart. On a modern piano or other equal-tempered instrument, all the half steps are the same size...
in just intonation in many ways, all of which make certain chords purely tuned and as consonant and stable as possible, and the other chords not accommodated and considerably less stable.
The prominent notes of a given scale are tuned so that their frequencies form ratios of relatively small integers. For example, in the key of G major
G major
G major is a major scale based on G, with the pitches G, A, B, C, D, E, and F. Its key signature has one sharp, F; in treble-clef key signatures, the sharp-symbol for F is usually placed on the first line from the top, though in some Baroque music it is placed on the first space from the bottom...
, the ratio of the frequencies of the notes G to D (a perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
) is 3/2, while that of G to C (a perfect fourth
Perfect fourth
In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
) is 4/3. Three basic intervals can be used to construct any interval involving the prime numbers 2, 3, and 5 (known as 5-limit just intonation):
- s = 16:15 (SemitoneSemitoneA semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
) - t = 10:9 (Minor tone)
- T = 9:8 (Major tone)
which combine to form:
- 6:5 = Ts (minor third)
- 5:4 = Tt (major third)
- 4:3 = Tts (perfect fourth)
- 3:2 = TTts (perfect fifth)
- 2:1 = TTTttss (octave)
A just diatonic scale may be derived as follows. Suppose we insist that the chords F-A-C, C-E-G, and G-B-D be just major triads
Major chord
In music theory, a major chord is a chord having a root, a major third, and a perfect fifth. When a chord has these three notes alone, it is called a major triad...
(then A-C-E and E-G-B are just minor triads
Minor chord
In music theory, a minor chord is a chord having a root, a minor third, and a perfect fifth.When a chord has these three notes alone, it is called a minor triad....
, but D-F-A is not).
Then we obtain this scale:
| Note | Name | C | D | E | F | G | A | B | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 | |||||||||
| Natural | 24 | 27 | 30 | 32 | 36 | 40 | 45 | 48 | |||||||||
| Cents | 0 | 204 | 386 | 498 | 702 | 884 | 1088 | 1200 | |||||||||
| Step | Name | T | t | s | T | t | T | s | |||||||||
| Ratio | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 | ||||||||||
| Cents | 204 | 182 | 112 | 204 | 182 | 204 | 112 | ||||||||||
The major thirds are correct, and two minor thirds are right, but D-F is a 32:27 semiditone. Others approaches are possible (see Five-limit tuning
Five-limit tuning
Five-limit tuning, or 5-limit tuning is a method to obtain a justly tuned musical scale. The frequencies of the notes of such a scale are obtained by multiplying the frequency of a given reference note by powers of 2, 3, or 5, or a combination of them...
), but it is impossible to get all six above-mentioned chords correct. Concerning triads, the triads on I, IV, and V are 4:5:6, the triad on ii is 27:32:40, the triads on iii and vi are 10:12:15, and the triad on vii is 45:54:64.
Pythagorean tuning
The oldest known form of tuning, Pythagorean tuningPythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
, can produce a twelve tone scale, but it does so by involving ratios of very large numbers, corresponding to natural harmonics very high in the harmonic series that do not occur widely in physical phenomena. This tuning uses ratios involving only powers of 3 and 2, creating a sequence of just fifths
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
or fourth
Perfect fourth
In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
s, as follows:
| Note | G | D | A | E | B | F | C | G | D | A | E | B | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Cents | 588 | 90 | 792 | 294 | 996 | 498 | 0 | 702 | 204 | 906 | 408 | 1110 | 612 |
The ratios are computed with respect to C (the base note). Starting from C, they are obtained by moving six steps to the left and six to the right. Each step consists of a multiplication of the previous pitch by 2/3 (descending fifth), 3/2 (ascending fifth), or their inversions
Inversion (music)
In music theory, the word inversion has several meanings. There are inverted chords, inverted melodies, inverted intervals, and inverted voices...
(3/4 or 4/3).
Between the enharmonic
Enharmonic
In modern musical notation and tuning, an enharmonic equivalent is a note , interval , or key signature which is equivalent to some other note, interval, or key signature, but "spelled", or named, differently...
notes at both ends of this sequence, is a difference in pitch
Pitch (music)
Pitch is an auditory perceptual property that allows the ordering of sounds on a frequency-related scale.Pitches are compared as "higher" and "lower" in the sense associated with musical melodies,...
of about 24 cents
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...
, known as the Pythagorean comma
Pythagorean comma
In musical tuning, the Pythagorean comma , named after the ancient mathematician and philosopher Pythagoras, is the small interval existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B , or D and C...
, much closer to the unison
Unison
In music, the word unison can be applied in more than one way. In general terms, it may refer to two notes sounding the same pitch, often but not always at the same time; or to the same musical voice being sounded by several voices or instruments together, either at the same pitch or at a distance...
(0 cents) than to the semitone
Semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
(100 cents). Thus, the two notes sound almost identical. To produce a twelve tone scale, one of them is arbitrarily discarded. The twelve remaining notes are repeated by increasing or decreasing their frequencies by a multiple of 2 (the size of one or more octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
s) to build scales with multiple octaves (such as the keyboard of a piano). A drawback of Pythagorean tuning is that one of the twelve fifths in this scale is badly tuned and hence unusable (the wolf fifth, either F-D if G is discarded, or B-G if F is discarded). This twelve tone scale is fairly close to equal temperament
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
, but it does not offer much advantage for tonal
Tonality
Tonality is a system of music in which specific hierarchical pitch relationships are based on a key "center", or tonic. The term tonalité originated with Alexandre-Étienne Choron and was borrowed by François-Joseph Fétis in 1840...
harmony because only the perfect intervals (fourth, fifth, and octave) are simple enough to sound pure. Major thirds, for instance, receive the rather unstable interval of 81/64, sharp of the preferred 5/4 by an 81/80 ratio. The primary reason for its use is that it is extremely easy to tune, as its building block, the perfect fifth, is the simplest and consequently the most consonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
interval after the octave and unison.
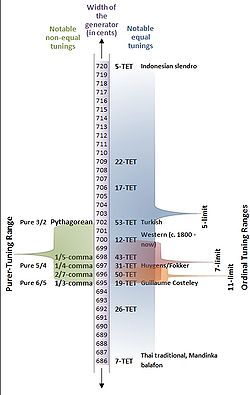
Pythagorean tuning may be regarded as a "3-limit" tuning system, because the ratios are obtained by using only powers of n, where n is at most 3.
Quarter-comma meantone
The quarter-comma meantoneQuarter-comma meantone
Quarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning...
tuning system uses a similar sequence of fifths to produce a twelve tone scale. However, it flattens the fifths by about 5.38 cents with respect to their just intonation, in order to generate justly tuned major thirds (with interval ratio 5:4).
Although this tuning system is based on a just ratio (5:4), it cannot be considered a just intonation system, because most of its intervals are irrational numbers (i.e. they cannot be expressed as fractions of integers). For instance:
- the ratio of most semitones is

- the ratio of most tones is

- the ratio of most fifths is

5-limit tuning
A twelve tone scale can also be created by compounding harmonics up to the fifth. Namely, by multiplying the frequency of a given reference note (the base note) by powers of 2, 3, or 5, or a combination of them. This method is called five-limit tuning.To build such a twelve tone scale, we may start by constructing a table containing fifteen pitches:
| Factor | 1/9 | 1/3 | 1 | 3 | 9 | |
|---|---|---|---|---|---|---|
| 5 | note ratio cents |
D 10/9 182 |
A 5/3 884 |
E 5/4 386 |
B 15/8 1088 |
F 45/32 590 |
| 1 | note ratio cents |
B 16/9 996 |
F 4/3 498 |
C 1 0 |
G 3/2 702 |
D 9/8 204 |
| 1/5 | note ratio cents |
G 64/45 610 |
D 16/15 112 |
A 8/5 814 |
E 6/5 316 |
B 9/5 1018 |
The factors listed in the first row and column are powers of 3 and 5, respectively (e.g., 1/9 = 3−2). Colors indicate couples of enharmonic
Enharmonic
In modern musical notation and tuning, an enharmonic equivalent is a note , interval , or key signature which is equivalent to some other note, interval, or key signature, but "spelled", or named, differently...
notes with almost identical pitch. The ratios are all expressed relative to C in the centre of this diagram (the base note for this scale). They are computed in two steps:
- For each cell of the table, a base ratio is obtained by multiplying the corresponding factors. For instance, the base ratio for the lower-left cell is 1/9 · 1/5 = 1/45.
- The base ratio is then multiplied by a negative or positive power of 2, as large as needed to bring it within the range of the octave starting from C (from 1/1 to 2/1). For instance, the base ratio for the lower left cell (1/45) is multiplied by 25, and the resulting ratio is 64/45, which is a number between 1/1 and 2/1.
Note that the powers of 2 used in the second step may be interpreted as ascending or descending octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
s. For instance, multiplying the frequency of a note by 25 means increasing it by 5 octaves. Moreover, each row of the table may be considered to be a sequence of fifths (ascending to the right), and each column a sequence of major thirds (ascending upward). For instance, in the first row of the table, there is an ascending fifth from D and A, and another one (followed by a descending octave) from A to E. This suggests an alternative but equivalent method for computing the same ratios. For instance, you can obtain A, starting from C, by moving one cell to the left and one upward in the table, which means descending by a fifth and ascending by a major third:

Since this is below C, you need to move up by an octave to end up within the desired range of ratios (from 1/1 to 2/1):

A 12 tone scale is obtained by removing one note for each couple of enharmonic notes. This can be done in at least three ways, which have in common the removal of G, according to a convention which was valid even for C-based Pythagorean and 1/4-comma meantone scales. We show here only one of the possible strategies (the others are discussed in 5-limit tuning). It consists of discarding the first column of the table (labeled "1/9"). The resulting 12-tone scale is shown below:
| Asymmetric scale | ||||||
|---|---|---|---|---|---|---|
| Factor | 1/3 | 1 | 3 | 9 | ||
| 5 | A 5/3 |
E 5/4 |
B 15/8 |
F 45/32 |
||
| 1 | F 4/3 |
C 1 |
G 3/2 |
D 9/8 |
||
| 1/5 | D 16/15 |
A 8/5 |
E 6/5 |
B 9/5 |
||
Extension of the twelve tone scale
The table above uses only low powers of 3 and 5 to build the base ratios. However, it can be easily extended by using higher positive and negative powers of the same numbers, such as 52 = 25, 5−2 = 1/25, 33 = 27, or 3−3 = 1/27. A scale with 25, 35 or even more pitches can be obtained by combining these base ratios (see Five-limit tuningFive-limit tuning
Five-limit tuning, or 5-limit tuning is a method to obtain a justly tuned musical scale. The frequencies of the notes of such a scale are obtained by multiplying the frequency of a given reference note by powers of 2, 3, or 5, or a combination of them...
for further details).
Indian scales
In Indian musicMusic of India
The music of India includes multiple varieties of folk, popular, pop, classical music and R&B. India's classical music tradition, including Carnatic and Hindustani music, has a history spanning millennia and developed over several eras. It remains fundamental to the lives of Indians today as...
, the just diatonic scale described above is used, though there are different possibilities, for instance for the 6th pitch (Dha), and further modifications may be made to all pitches excepting Sa and Pa.
| Note | Sa | Re | Ga | Ma | Pa | Dha | Ni | Sa |
|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 or 27/16 | 15/8 | 2/1 |
| Cents | 0 | 204 | 386 | 498 | 702 | 884 or 906 | 1088 | 1200 |
Some accounts of Indian intonation system cite a given 22 Śrutis. According to some musicians, you have a scale of a given 12 pitches and ten in addition (the tonic, Shadja (Sa), and the pure fifth, Pancham (Pa), are inviolate):
| Note | C | D | D | E | E | F | F | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Cents | 0 | 90 | 112 | 182 | 204 | 294 | 316 | 386 | 408 | 498 | 520 | 590 |
| Note | G | A | A | B | B | C | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Cents | 610 | 702 | 792 | 814 | 884 | 906 | 996 | 1018 | 1088 | 1110 | 1200 |
Where we have two ratios for a given letter name, we have a difference of 81:80 (or 22 cents), which is known as the syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
. You can see the symmetry, looking at it from the tonic, then the octave.
(This is just one example of "explaining" a 22-Śruti scale of tones. There are many different explanations.)
Practical difficulties
Some fixed just intonation scales and systems, such as the diatonic scale above, produce wolf intervalWolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
s. The above scale allows a minor tone to occur next to a semitone which produces the awkward ratio 32:27 for F:D, and still worse, a minor tone next to a fourth giving 40:27 for A:D. Moving D down to 10/9 alleviates these difficulties but creates new ones: G:D becomes 27:20, and B:G becomes 27:16.
You can have more fret
Fret
A fret is a raised portion on the neck of a stringed instrument, that extends generally across the full width of the neck. On most modern western instruments, frets are metal strips inserted into the fingerboard...
s on a guitar
Guitar
The guitar is a plucked string instrument, usually played with fingers or a pick. The guitar consists of a body with a rigid neck to which the strings, generally six in number, are attached. Guitars are traditionally constructed of various woods and strung with animal gut or, more recently, with...
to handle both A's, 9/8 with respect to G and 10/9 with respect to G so that C:A can be played as 6:5 while D:A can still be played as 3:2. 9/8 and 10/9 are less than 1/53 octave apart, so mechanical and performance considerations have made this approach extremely rare. And the problem of how to tune chords such as C-E-G-A-D is left unresolved (for instance, A could be 4:3 below D (making it 9/8, if G is 1) or 4:3 above E (making it 10/9, if G is 1) but not both at the same time, so one of the fourths in the chord will have to be an out-of-tune wolf interval). However the frets may be removed entirely—this, unfortunately, makes in-tune fingering of many chords exceedingly difficult, due to the construction and mechanics of the human hand—and the tuning of most complex chords in just intonation is generally ambiguous.
Some composers deliberately use these wolf intervals and other dissonant intervals as a way to expand the tone color palette of a piece of music. For example, the extended piano pieces "The Well-Tuned Piano" by LaMonte Young, and "The Harp Of New Albion" by Terry Riley use a combination of very consonant and dissonant intervals for musical effect. In "Revelation," Michael Harrison goes even farther, and uses the tempo of beat patterns produced by some dissonant intervals as an integral part of several movements.
For many instruments tuned in just intonation, you can't change keys
Key (music)
In music theory, the term key is used in many different and sometimes contradictory ways. A common use is to speak of music as being "in" a specific key, such as in the key of C major or in the key of F-sharp. Sometimes the terms "major" or "minor" are appended, as in the key of A minor or in the...
without retuning your instrument. For instance, if you tune a piano to just intonation intervals and a minimum of wolf intervals for the key of G, then only one other key (typically E-flat) can have the same intervals, and many of the keys have a very dissonant and unpleasant sound. This makes modulation
Modulation (music)
In music, modulation is most commonly the act or process of changing from one key to another. This may or may not be accompanied by a change in key signature. Modulations articulate or create the structure or form of many pieces, as well as add interest...
within a piece, or playing a repertoire of pieces in different keys, impractical to impossible.
Synthesizer
Synthesizer
A synthesizer is an electronic instrument capable of producing sounds by generating electrical signals of different frequencies. These electrical signals are played through a loudspeaker or set of headphones...
s have proven a valuable tool for composers wanting to experiment with just intonation. Many commercial synthesizers provide the ability to use built-in just intonation scales or to program your own. Wendy Carlos
Wendy Carlos
Wendy Carlos is an American composer and electronic musician. Carlos first came to notice in the late 1960s with recordings made on the Moog synthesizer, then a relatively new and unknown instrument; most notable were LPs of synthesized Bach and the soundtrack for Stanley Kubrick's film A...
used a system on her 1986 album Beauty in the Beast
Beauty in the Beast
Beauty in the Beast is an album by Wendy Carlos using alternate tunings and scales and influenced by jazz and world music. On the back she includes a quote by Van Gogh: "I am always doing what I cannot do yet, in order to learn how to do it."...
, where one electronic keyboard was used to play the notes, and another used to instantly set the root note to which all intervals were tuned, which allowed for modulation. On her 1987 lecture album Secrets of Synthesis there are audible examples of the difference in sound between equal temperament and just intonation.
Singing
The human voice is among the most pitch-flexible instruments in common use. Pitch can be varied with no restraints and adjusted in the midst of performance, without needing to retune (as even with the otherwise flexible string instruments). Although the explicit use of just intonation fell out of favour concurrently with the increasing use of instrumental accompaniment (with its attendant constraints on pitch), most a cappellaA cappella
A cappella music is specifically solo or group singing without instrumental sound, or a piece intended to be performed in this way. It is the opposite of cantata, which is accompanied singing. A cappella was originally intended to differentiate between Renaissance polyphony and Baroque concertato...
ensembles naturally tend toward just intonation because of the comfort of its stability. Barbershop quartets
Barbershop music
Barbershop vocal harmony, as codified during the barbershop revival era , is a style of a cappella, or unaccompanied vocal music characterized by consonant four-part chords for every melody note in a predominantly homophonic texture...
are a good example of this.
Western composers
Most composers don't specify how instruments are to be tuned, although historically most have assumed one tuning system which was common in their time; in the 20th century most composers assumed equal temperamentEqual temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
would be used. However, a few have specified just intonation systems for some or all of their compositions, including John Adams
John Coolidge Adams
John Coolidge Adams is a Pulitzer Prize-winning American composer with strong roots in minimalism. His best-known works include Short Ride in a Fast Machine , On the Transmigration of Souls , a choral piece commemorating the victims of the September 11, 2001 attacks , and Shaker...
, Glenn Branca
Glenn Branca
Glenn Branca is an American avant-garde composer and guitarist known for his use of volume, alternative guitar tunings, repetition, droning, and the harmonic series. In 2008 he was awarded an unrestricted grant from the Foundation for Contemporary Arts.-Beginnings: 1960s and early 1970s:Branca...
, Martin Bresnick
Martin Bresnick
Martin Bresnick is a composer of contemporary classical music, film scores and experimental music.-Education and early career:Bresnick was born and raised in the Bronx, and is a graduate of New York City's specialized High School of Music and Art. He was educated at the University of Hartford ,...
, Wendy Carlos
Wendy Carlos
Wendy Carlos is an American composer and electronic musician. Carlos first came to notice in the late 1960s with recordings made on the Moog synthesizer, then a relatively new and unknown instrument; most notable were LPs of synthesized Bach and the soundtrack for Stanley Kubrick's film A...
, Lawrence Chandler
Lawrence Chandler
Lawrence Chandler is an American-born musician, composer and sound artist living in London. He studied with La Monte Young, Pauline Oliveros, at The Juilliard School and Goldsmiths College. He was a founder member of Bowery Electric and has worked for Philip Glass.-References:...
, Tony Conrad
Tony Conrad
Tony Conrad is an American avant-garde video artist, experimental filmmaker, musician/composer, sound artist, teacher and writer...
, Stuart Dempster
Stuart Dempster
Stuart Dempster is a trombonist, didjeridu player, improvisor, and composer.-Biography:After Dempster completed his studies at San Francisco State College, he was appointed assistant professor at the California State College at Hayward, and instructor at the San Francisco Conservatory...
, David B. Doty
David B. Doty
David B. Doty is an American composer and authority on just intonation. He is the author of The Just Intonation Primer ....
, Arnold Dreyblatt
Arnold Dreyblatt
Arnold Dreyblatt is an American composer and visual artist. He studied music with Pauline Oliveros, La Monte Young, Alvin Lucier and media art with Steina and Woody Vasulka. He has been based in Berlin, Germany since 1984...
, Kyle Gann
Kyle Gann
Kyle Eugene Gann is an American professor of music, critic and composer born in Dallas, Texas. As a critic for The Village Voice and other publications he has been a supporter of progressive music including such Downtown movements as postminimalism and totalism.- As composer :As a composer his...
, Kraig Grady
Kraig Grady
Kraig Grady is a US-Australian composer/sound artist. He has composed and performed with an ensemble of microtonal instruments of his own design and also worked as a shadow puppeteer, tuning theorist, filmmaker, world music radio DJ and concert promoter...
, Lou Harrison
Lou Harrison
Lou Silver Harrison was an American composer. He was a student of Henry Cowell, Arnold Schoenberg, and K. P. H. Notoprojo Lou Silver Harrison (May 14, 1917 – February 2, 2003) was an American composer. He was a student of Henry Cowell, Arnold Schoenberg, and K. P. H. Notoprojo Lou Silver Harrison...
, Ben Johnston, Elodie Lauten
Elodie Lauten
Elodie Lauten is a composer described as postminimalist or a microtonalist.-Biography:Born in Paris, France, Lauten was classically trained as a pianist since age 7. She received a Master's in composition from New York University where she studied Western composition with Dinu Ghezzo and Indian...
, György Ligeti
György Ligeti
György Sándor Ligeti was a composer of contemporary classical music. Born in a Hungarian Jewish family in Transylvania, Romania, he briefly lived in Hungary before becoming an Austrian citizen.-Early life:...
, Douglas Leedy
Douglas Leedy
Douglas Leedy is an American composer, performer and music scholar.-Biography:Born in Portland, Oregon, Leedy studied with Karl Kohn at Pomona College and at the University of California, Berkeley, where he was in a composition seminar with membership including La Monte Young and Terry Riley...
, Pauline Oliveros
Pauline Oliveros
Pauline Oliveros is an American accordionist and composer who is a central figure in the development of post-war electronic art music....
, Harry Partch
Harry Partch
Harry Partch was an American composer and instrument creator. He was one of the first twentieth-century composers to work extensively and systematically with microtonal scales, writing much of his music for custom-made instruments that he built himself, tuned in 11-limit just intonation.-Early...
, Robert Rich
Robert Rich (musician)
Robert Rich is an ambient musician and composer based in California, United States. With a discography spanning over 30 years, he is widely regarded as a figure whose sound has greatly influenced today's ambient, New Age, and even IDM music.-Early life:At an early age he thought he disliked music...
, Terry Riley
Terry Riley
Terrence Mitchell Riley, is an American composer intrinsically associated with the minimalist school of Western classical music and was a pioneer of the movement...
, Marc Sabat
Marc Sabat
Marc Sabat is a Canadian composer based in Berlin since 1999.-Works:He has made installations, video works and concert music pieces using acoustic instruments and, in some recent pieces, computer-generated electronics, drawing inspiration from investigations of the sounding and perception of small...
, Wolfgang von Schweinitz
Wolfgang von Schweinitz
Wolfgang von Schweinitz is a German composer of classical music.Schweinitz studied composition at the Hochschule für Musik und Theater Hamburg, from 1971 to 1973 with Gernot Klussmann and from 1973 to 1975 with György Ligeti. He continued his studies at the Stanford University with John Chowning...
, Adam Silverman
Adam Silverman
Adam Benjamin Silverman is a composer of contemporary classical music. His works include the opera Korczak's Orphans , chamber and orchestral music, and music for the theater...
, James Tenney
James Tenney
James Tenney was an American composer and influential music theorist.-Biography:Tenney was born in Silver City, New Mexico, and grew up in Arizona and Colorado. He attended the University of Denver, the Juilliard School of Music, Bennington College and the University of Illinois...
, Daniel James Wolf
Daniel James Wolf
Daniel James Wolf is an American composer.- Studies :Wolf studied composition with Gordon Mumma, Alvin Lucier, and La Monte Young, as well as musical tunings with Erv Wilson and Douglas Leedy and ethnomusicology . Important contacts with Lou Harrison, John Cage, Walter Zimmermann...
, and La Monte Young
La Monte Young
La Monte Thornton Young is an American avant-garde composer, musician, and artist.Young is generally recognized as the first minimalist composer. His works have been included among the most important and radical post-World War II avant-garde, experimental, and contemporary music. Young is...
. Eivind Groven
Eivind Groven
Eivind Groven was a Norwegian microtonal composer and music-theorist. He was from Telemark and had his background in the folk music of the area.- Biography :...
is often considered a just intonation composer but just intonation purists will disagree. His tuning system was in fact schismatic temperament
Schismatic temperament
The schismatic temperament is a musical tuning system that results from tempering the schisma of 32805:32768 to a unison. It is also called the schismic temperament or Helmholtz temperament.-Comparison with other tunings:...
, which is indeed capable of far closer approximations to just intonation consonances than 12-note equal temperament or even meantone temperament
Meantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
, but still alters the pure ratios of just intonation slightly in order to achieve a simpler and more flexible system than true just intonation.
Music written in just intonation is most often tonal
Tonality
Tonality is a system of music in which specific hierarchical pitch relationships are based on a key "center", or tonic. The term tonalité originated with Alexandre-Étienne Choron and was borrowed by François-Joseph Fétis in 1840...
but need not be; some music of Kraig Grady and Daniel James Wolf uses just intonation scales designed by Erv Wilson
Erv Wilson
Ervin Wilson is a Mexican/American music theorist. Despite his avoidance of academia, Wilson has been influential on those interested in microtonal music and just intonation, especially in the areas of scale, keyboard, and notation design...
explicitly for a consonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
form of atonality
Atonality
Atonality in its broadest sense describes music that lacks a tonal center, or key. Atonality in this sense usually describes compositions written from about 1908 to the present day where a hierarchy of pitches focusing on a single, central tone is not used, and the notes of the chromatic scale...
, and Ben Johnston's Sonata for Microtonal Piano
Sonata for Microtonal Piano
Sonata for Microtonal Piano is a sonata for specifically microtonally tuned piano by Ben Johnston written in 1964 .The composer is trying to escape the "standard" forms of music; in the words of the composer:-Grindlemusic:...
(1964) uses serialism
Serialism
In music, serialism is a method or technique of composition that uses a series of values to manipulate different musical elements. Serialism began primarily with Arnold Schoenberg's twelve-tone technique, though his contemporaries were also working to establish serialism as one example of...
to achieve an atonal result. Composers often impose a limit
Limit (music)
In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name...
on how complex the ratios used are: for example, a composer may write in "7-limit JI", meaning that no prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
larger than 7 features in the ratios they use. Under this scheme, the ratio 10/7, for example, would be permitted, but 11/7 would not be, as all non-prime numbers are octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
s of, or mathematically and tonally related to, lower primes (example: 12 is a double octave of 3, while 9 is a square of 3). Yuri Landman
Yuri Landman
Yuri Landman is a Dutch experimental luthier who has made several experimental electric string instruments for a list of artists including Lee Ranaldo of Sonic Youth, Liars, Jad Fair of Half Japanese and Liam Finn...
derived a just intoned musical scale from a initially considered atonal prepared guitar
Prepared guitar
A prepared guitar is a guitar that has had its timbre altered by placing various objects on or between the instrument's strings, including other extended techniques...
playing technique
Extended technique
Extended techniques are performance techniques used in music to describe unconventional, unorthodox, or non-traditional techniques of singing, or of playing musical instruments to obtain unusual sounds or instrumental timbres....
based on adding a third bridge
Bridge (instrument)
A bridge is a device for supporting the strings on a stringed instrument and transmitting the vibration of those strings to some other structural component of the instrument in order to transfer the sound to the surrounding air.- Explanation :...
under the strings. When this bridge is positioned in the noded
Node (physics)
A node is a point along a standing wave where the wave has minimal amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effective length of the vibrating string and thereby the...
positions of the harmonic series
Harmonic series (music)
Pitched musical instruments are often based on an approximate harmonic oscillator such as a string or a column of air, which oscillates at numerous frequencies simultaneously. At these resonant frequencies, waves travel in both directions along the string or air column, reinforcing and canceling...
the volume of the instrument increases and the overtone
Overtone
An overtone is any frequency higher than the fundamental frequency of a sound. The fundamental and the overtones together are called partials. Harmonics are partials whose frequencies are whole number multiples of the fundamental These overlapping terms are variously used when discussing the...
becomes clear and has a consonant relation to the complementary opposed string part creating a harmonic multiphonic
Multiphonic
Multiphonics is an extended technique in instrumental music in which a monophonic instrument is made to produce several notes at once....
tone.
Staff notation
Recently some composers have been developing notation methods for Just Intonation using the conventional five-line staff. James TenneyJames Tenney
James Tenney was an American composer and influential music theorist.-Biography:Tenney was born in Silver City, New Mexico, and grew up in Arizona and Colorado. He attended the University of Denver, the Juilliard School of Music, Bennington College and the University of Illinois...
, amongst others, preferred to combine JI ratios with cents
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...
deviations from the equal tempered pitches, indicated in a legend or directly in the score, allowing performers to readily use electronic tuning devices if desired. Beginning in the 1960s, Ben Johnston had proposed an alternative approach, redefining the understanding of conventional symbols (the seven "white" notes, the sharps and flats) and adding further accidentals, each designed to extend the notation into higher prime limits. Johnston‘s method is based on a diatonic C Major scale tuned in JI, in which the interval between D (9/8 above C) and A (5/3 above C) is one Syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
less than a Pythagorean perfect fifth 3:2. To write a perfect fifth, Johnston introduces a pair of symbols representing this comma, + and -. Thus, a series of perfect fifths beginning with F would proceed C G D A+ E+ B+. The three conventional white notes A E B are tuned as Ptolemaic major thirds (5:4) above F C G respectively. Johnston introduces new symbols for the septimal, undecimal, tridecimal, and further prime extensions to create an accidental based exact JI notation for what he has named "Extended Just Intonation".
In the years 2000-2004, Marc Sabat
Marc Sabat
Marc Sabat is a Canadian composer based in Berlin since 1999.-Works:He has made installations, video works and concert music pieces using acoustic instruments and, in some recent pieces, computer-generated electronics, drawing inspiration from investigations of the sounding and perception of small...
and Wolfgang von Schweinitz
Wolfgang von Schweinitz
Wolfgang von Schweinitz is a German composer of classical music.Schweinitz studied composition at the Hochschule für Musik und Theater Hamburg, from 1971 to 1973 with Gernot Klussmann and from 1973 to 1975 with György Ligeti. He continued his studies at the Stanford University with John Chowning...
worked together in Berlin to develop a different accidental based method, the Extended Helmholtz-Ellis JI Pitch Notation. Following the method of notation suggested by Helmholtz in his classic "On the Sensations of Tone as a Physiological Basis for the Theory of Music", incorporating Ellis' invention of cents, and following Johnston's step into "Extended JI", Sabat and Schweinitz consider each prime dimension of harmonic space to be represented by a unique symbol. In particular they take the conventional flats, naturals and sharps as a Pythagorean series of perfect fifths. Thus, a series of perfect fifths beginning with F proceeds C G D A E B F# and so on. The advantage for musicians is that conventional reading of the basic fourths and fifths remains familiar. Such an approach has also been advocated by Daniel James Wolf
Daniel James Wolf
Daniel James Wolf is an American composer.- Studies :Wolf studied composition with Gordon Mumma, Alvin Lucier, and La Monte Young, as well as musical tunings with Erv Wilson and Douglas Leedy and ethnomusicology . Important contacts with Lou Harrison, John Cage, Walter Zimmermann...
. In the Sabat-Schweinitz design, Syntonic Commas are marked by arrows attached to the flat, natural or sharp sign, Septimal Commas using Giuseppe Tartini's symbol, and Undecimal Quartertones using the common practice quartertone signs (a single cross and backwards flat). For higher primes, additional signs have been designed. To facilitate quick estimation of pitches, cents indications may be added (downward deviations below and upward deviations above the respective accidental). The convention used is that the cents written refer to the tempered pitch implied by the flat, natural, or sharp sign and the note name. One of the great advantages of such a notation is that it allows the natural harmonic series to be precisely notated. A complete legend and fonts for the notation (see samples) are open source and available from PLAINSOUND MUSIC EDITION.
See also
- Equal temperamentEqual temperamentAn equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
- Mathematics of musical scales
- Microtonal musicMicrotonal musicMicrotonal music is music using microtones—intervals of less than an equally spaced semitone. Microtonal music can also refer to music which uses intervals not found in the Western system of 12 equal intervals to the octave.-Terminology:...
- MicrotunerMicrotunerA microtuner or microtonal tuner is an electronic device or software program designed to modify and test the tuning of musical instruments with microtonal precision, allowing for the design and construction of microtonal scales and just intonation scales, and for tuning intervals that differ from...
- Pythagorean intervalPythagorean intervalIn musical tuning theory, a Pythagorean interval is a musical interval with frequency ratio equal to a power of two divided by a power of three, or vice versa...
- SemitoneSemitoneA semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
- List of intervals in 5-limit just intonation
- List of meantone intervals
- List of musical intervals
- Whole-tone scale
- Regular numberRegular numberRegular numbers are numbers that evenly divide powers of 60. As an example, 602 = 3600 = 48 × 75, so both 48 and 75 are divisors of a power of 60...
- HexanyHexanyIn music theory, the hexany is a six-note just intonation scale, with the notes placed on the vertices of an octahedron, equivalently the faces of a cube...
- Electronic tunerElectronic tunerThe term electronic tuner can refer to a number of different things, depending which discipline you wish to study.In the Discipline of radio frequency electronics an electronic tuner is a device which tunes across a part of the radio frequency spectrum by the application of a voltage or appropriate...
- Consonance and dissonanceConsonance and dissonanceIn music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
External links
- Art of the States: microtonal/just intonation works using just intonation by American composers
- The Chrysalis Foundation -- Just Intonation: Two Definitions
- Dante Rosati's 21 Tone Just Intonation guitar
- Just Intonation by Mark Nowitzky
- Just intonation compared with meantoneMeantone temperamentMeantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
and 12-equalEqual temperamentAn equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
temperaments; a video featuring Pachelbel's canon. - Just Intonation Explained by Kyle GannKyle GannKyle Eugene Gann is an American professor of music, critic and composer born in Dallas, Texas. As a critic for The Village Voice and other publications he has been a supporter of progressive music including such Downtown movements as postminimalism and totalism.- As composer :As a composer his...
- Just Intonation Network
- A selection of Just Intonation works edited by the Just Intonation Network web published on the Tellus Audio Cassette MagazineTellus Audio Cassette MagazineLaunched from the Lower East Side, Manhattan, in 1983 as a subscription only bimonthly publication, the Tellus cassette series took full advantage of the popular cassette medium to promote cutting-edge downtown music, documenting the New York scene and advancing experimental composers of the time...
project archive at UbuwebUbuWebUbuWeb is a large web-based educational resource for avant-garde material available on the internet, founded in 1996 by poet Kenneth Goldsmith. It offers visual, concrete and sound poetry, expanding to include film and sound art mp3 archives.-Philosophy:... - Medieval Music and Arts Foundation
- Music Novatory - Just Intonation
- Why does Just Intonation sound so good?
- The Wilson Archives
- Barbieri, Patrizio. Enharmonic instruments and music, 1470-1900. (2008) Latina, Il Levante
- 22 Note Just Intonation Keyboard Software with 12 Indian Instrument Sounds Libreria Editrice
- PLAINSOUND MUSIC EDITION - JI music and research, information about the Helmholtz-Ellis JI Pitch Notation

