
Syntonic comma
Encyclopedia
In music theory
, the syntonic comma, also known as the chromatic diesis, the comma of Didymus
, the Ptolemaic
comma, or the diatonic comma is a small comma
type interval
between two musical note
s, equal to the frequency ratio 81:80, or around 21.51 cent
s. Two notes that differ by this interval would sound different from each other even to untrained ears, but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is referred to as Didymus
' because it is the amount by which Didymus corrected the Pythagorean
major third
to a just
major third (81:64 or 407.82 cents - 21.51 = 386.31 cents or 5:4).
Composer Ben Johnston uses a "−" as an accidental to indicate a note is lowered 21.51 cents, or a "+" to indicate a note is raised 21.51 cents.
(81:64).
Another way of describing the syntonic comma, as a combination of more commonly encountered intervals, is the difference between four justly
tuned perfect fifth
s, and two octave
s plus a justly tuned major third
. A just perfect fifth has its notes in the frequency
ratio 3:2, which is equal to 701.955 cents, and four of them are equal to 2807.82 cents (81:16). A just major third has its notes in the frequency ratio 5:4, which is equal to 386.31 cents, and one of them plus two octaves is equal to 2786.31 cents (5:1 or 80:16). The difference between these is 21.51 cents (81:80), a syntonic comma.
Equally, it can be described as the difference between three justly tuned perfect fourth
s (64/27 or 1494.13 cents), and a justly tuned minor third
(6/5) an octave
higher (12/5 or 1515.64 cents).
The difference of 21.51 cents has contemporary significance because on a piano
keyboard, four fifths is equal to two octaves plus a major third. Starting from a C, both combinations of intervals will end up at E. The fact that using justly tuned intervals yields two slightly different notes is one of the reasons compromises have to be made when deciding which system of musical tuning
to use for an instrument. Pythagorean tuning
tunes the fifths as exact 3:2s, but uses the relatively complex ratio of 81:64 for major thirds. Quarter-comma meantone
, on the other hand, uses exact 5:4s for major thirds, but flattens each of the fifths by a quarter of a syntonic comma. Other systems use different compromises.
In just intonation
, there are two kinds of major second
, called major and minor tone. In 5-limit just intonation, they have a ratio of 9:8 and 10:9, and the ratio between them is the syntonic comma (81:80). Also, 27:16 ÷ 5:3 = 81:80.
Mathematically, by Størmer's theorem
, 81:80 is the closest superparticular ratio possible with regular number
s as numerator and denominator. A superparticular ratio is one whose numerator is 1 greater than its denominator, such as 5:4, and a regular number is one whose prime factor
s are limited to 2, 3, and 5. Thus, although smaller intervals can be described within 5-limit tunings, they cannot be described as superparticular ratios.
Another frequently encountered comma is the Pythagorean comma
.
and its inversion, the perfect fourth
. The Pythagorean major third
(81:64) and minor third
(32:27) were dissonant
, and this prevented musicians from using triad
s and chord
s, forcing them for centuries to write music with relatively simple texture
. In late Middle Ages
, musicians realized that by slightly tempering the pitch of some notes, the Pythagorean thirds could be made consonant
. For instance, if you decrease by a syntonic comma (81:80) the frequency of E, C-E (a major third), and E-G (a minor third) become just. Namely, C-E is flattened to a justly intonated
ratio of

and at the same time E-G is sharpened to the just ratio of
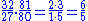
The drawback is that the fifths A-E and E-B, by flattening E, become almost as dissonant as the Pythagorean wolf fifth
. But the fifth C-G stays consonant, since only E has been flattened (C-E * E-G = 5/4 * 6/5 = 3/2), and can be used together with C-E to produce a C-major
triad (C-E-G). These experiments eventually brought to the creation of a new tuning system, known as quarter-comma meantone
, in which the number of major thirds was maximized, and most minor thirds were tuned to a ratio which was very close to the just 6:5. This result was obtained by flattening each fifth by a quarter of a syntonic comma, an amount which was considered negligible, and permitted the full development of music with complex texture
, such as polyphonic music
, or melody with instrumental accompaniment
. Since then, other tuning systems were developed, and the syntonic comma was used as a reference value to temper the perfect fifths in an entire family of them. Namely, in the family belonging to the syntonic temperament
continuum, including meantone temperament
s.
Music theory
Music theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
, the syntonic comma, also known as the chromatic diesis, the comma of Didymus
Didymus
Didymus may refer to:* Thomas the Apostle or "Didymus", both names meaning "twin" in Aramaic and Greek respectively, is the most well-known Didymus due to his role in early Christian history* Didymus Chalcenterus Didymus may refer to:* Thomas the Apostle or "Didymus", both names meaning "twin" in...
, the Ptolemaic
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
comma, or the diatonic comma is a small comma
Comma (music)
In music theory, a comma is a minute interval, the difference resulting from tuning one note two different ways. The word "comma" used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F tuned using the D-based Pythagorean tuning...
type interval
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
between two musical note
Note
In music, the term note has two primary meanings:#A sign used in musical notation to represent the relative duration and pitch of a sound;#A pitched sound itself....
s, equal to the frequency ratio 81:80, or around 21.51 cent
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...
s. Two notes that differ by this interval would sound different from each other even to untrained ears, but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is referred to as Didymus
Didymus the Musician
Didymus the Musician was a music theorist in Rome of the end of the 1st century BC or beginning of the 1st century AD, who combined elements of earlier theoretical approaches with an appreciation of the aspect of performance...
' because it is the amount by which Didymus corrected the Pythagorean
Pythagorean interval
In musical tuning theory, a Pythagorean interval is a musical interval with frequency ratio equal to a power of two divided by a power of three, or vice versa...
major third
Major third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
to a just
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
major third (81:64 or 407.82 cents - 21.51 = 386.31 cents or 5:4).
Composer Ben Johnston uses a "−" as an accidental to indicate a note is lowered 21.51 cents, or a "+" to indicate a note is raised 21.51 cents.
Relationships
The syntonic comma is the interval between a just major third (5:4) and a Pythagorean ditoneDitone
In music, a ditone is the interval 81:64, which is 407.82 cents. It is the major third in Pythagorean tuning. The ditone is evenly divisible by two major tones and is wider than a just major third by a syntonic comma...
(81:64).
Another way of describing the syntonic comma, as a combination of more commonly encountered intervals, is the difference between four justly
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
tuned perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
s, and two octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
s plus a justly tuned major third
Major third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
. A just perfect fifth has its notes in the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
ratio 3:2, which is equal to 701.955 cents, and four of them are equal to 2807.82 cents (81:16). A just major third has its notes in the frequency ratio 5:4, which is equal to 386.31 cents, and one of them plus two octaves is equal to 2786.31 cents (5:1 or 80:16). The difference between these is 21.51 cents (81:80), a syntonic comma.
Equally, it can be described as the difference between three justly tuned perfect fourth
Perfect fourth
In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
s (64/27 or 1494.13 cents), and a justly tuned minor third
Minor third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major...
(6/5) an octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
higher (12/5 or 1515.64 cents).
The difference of 21.51 cents has contemporary significance because on a piano
Piano
The piano is a musical instrument played by means of a keyboard. It is one of the most popular instruments in the world. Widely used in classical and jazz music for solo performances, ensemble use, chamber music and accompaniment, the piano is also very popular as an aid to composing and rehearsal...
keyboard, four fifths is equal to two octaves plus a major third. Starting from a C, both combinations of intervals will end up at E. The fact that using justly tuned intervals yields two slightly different notes is one of the reasons compromises have to be made when deciding which system of musical tuning
Musical tuning
In music, there are two common meanings for tuning:* Tuning practice, the act of tuning an instrument or voice.* Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases.-Tuning practice:...
to use for an instrument. Pythagorean tuning
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
tunes the fifths as exact 3:2s, but uses the relatively complex ratio of 81:64 for major thirds. Quarter-comma meantone
Quarter-comma meantone
Quarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning...
, on the other hand, uses exact 5:4s for major thirds, but flattens each of the fifths by a quarter of a syntonic comma. Other systems use different compromises.
In just intonation
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
, there are two kinds of major second
Major second
In Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions...
, called major and minor tone. In 5-limit just intonation, they have a ratio of 9:8 and 10:9, and the ratio between them is the syntonic comma (81:80). Also, 27:16 ÷ 5:3 = 81:80.
Mathematically, by Størmer's theorem
Størmer's theorem
In number theory, Størmer's theorem, named after Carl Størmer, gives a finite bound on the number of consecutive pairs of smooth numbers that exist, for a given degree of smoothness, and provides a method for finding all such pairs using Pell equations...
, 81:80 is the closest superparticular ratio possible with regular number
Regular number
Regular numbers are numbers that evenly divide powers of 60. As an example, 602 = 3600 = 48 × 75, so both 48 and 75 are divisors of a power of 60...
s as numerator and denominator. A superparticular ratio is one whose numerator is 1 greater than its denominator, such as 5:4, and a regular number is one whose prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s are limited to 2, 3, and 5. Thus, although smaller intervals can be described within 5-limit tunings, they cannot be described as superparticular ratios.
Another frequently encountered comma is the Pythagorean comma
Pythagorean comma
In musical tuning, the Pythagorean comma , named after the ancient mathematician and philosopher Pythagoras, is the small interval existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B , or D and C...
.
Syntonic comma in the history of music
The syntonic comma has a crucial role in the history of music. It is the amount by which some of the notes produced in Pythagorean tuning were flattened or sharpened to produce just minor and major thirds. In Pythagorean tuning, the only highly consonant intervals were the perfect fifthPerfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
and its inversion, the perfect fourth
Perfect fourth
In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
. The Pythagorean major third
Major third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
(81:64) and minor third
Minor third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major...
(32:27) were dissonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
, and this prevented musicians from using triad
Triad (music)
In music and music theory, a triad is a three-note chord that can be stacked in thirds. Its members, when actually stacked in thirds, from lowest pitched tone to highest, are called:* the Root...
s and chord
Chord (music)
A chord in music is any harmonic set of two–three or more notes that is heard as if sounding simultaneously. These need not actually be played together: arpeggios and broken chords may for many practical and theoretical purposes be understood as chords...
s, forcing them for centuries to write music with relatively simple texture
Texture (music)
In music, texture is the way the melodic, rhythmic, and harmonic materials are combined in a composition , thus determining the overall quality of sound of a piece...
. In late Middle Ages
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
, musicians realized that by slightly tempering the pitch of some notes, the Pythagorean thirds could be made consonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
. For instance, if you decrease by a syntonic comma (81:80) the frequency of E, C-E (a major third), and E-G (a minor third) become just. Namely, C-E is flattened to a justly intonated
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
ratio of

and at the same time E-G is sharpened to the just ratio of
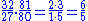
The drawback is that the fifths A-E and E-B, by flattening E, become almost as dissonant as the Pythagorean wolf fifth
Wolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
. But the fifth C-G stays consonant, since only E has been flattened (C-E * E-G = 5/4 * 6/5 = 3/2), and can be used together with C-E to produce a C-major
Major chord
In music theory, a major chord is a chord having a root, a major third, and a perfect fifth. When a chord has these three notes alone, it is called a major triad...
triad (C-E-G). These experiments eventually brought to the creation of a new tuning system, known as quarter-comma meantone
Quarter-comma meantone
Quarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning...
, in which the number of major thirds was maximized, and most minor thirds were tuned to a ratio which was very close to the just 6:5. This result was obtained by flattening each fifth by a quarter of a syntonic comma, an amount which was considered negligible, and permitted the full development of music with complex texture
Texture (music)
In music, texture is the way the melodic, rhythmic, and harmonic materials are combined in a composition , thus determining the overall quality of sound of a piece...
, such as polyphonic music
Polyphony
In music, polyphony is a texture consisting of two or more independent melodic voices, as opposed to music with just one voice or music with one dominant melodic voice accompanied by chords ....
, or melody with instrumental accompaniment
Homophony
In music, homophony is a texture in which two or more parts move together in harmony, the relationship between them creating chords. This is distinct from polyphony, in which parts move with rhythmic independence, and monophony, in which all parts move in parallel rhythm and pitch. A homophonic...
. Since then, other tuning systems were developed, and the syntonic comma was used as a reference value to temper the perfect fifths in an entire family of them. Namely, in the family belonging to the syntonic temperament
Syntonic temperament
The syntonic temperament is a system of musical tuning in which the frequency ratio of each musical interval is a product of powers of an octave and a tempered perfect fifth, with the width of the tempered major third being equal to four tempered perfect fifths minus two octaves and the width of...
continuum, including meantone temperament
Meantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
s.

