
Syntonic temperament
Encyclopedia
The syntonic temperament is a system of musical tuning in which the frequency ratio of each musical interval
is a product of powers of an octave
and a tempered perfect fifth
, with the width of the tempered major third
being equal to four tempered perfect fifths minus two octaves and the width of the tempered major second
being equal to two tempered perfect fifths minus one octave (i.e., half the width of the major third).
Alternatively put, the syntonic temperament:
This is the same definition as that of the meantone temperament
. The syntonic temperament can be viewed as a systematic extension of the meantone temperament beyond the range imposed by the meantone temperament's need to remain consonant with timbre
s that conform to the harmonic series
.
 The syntonic temperament is named after the syntonic comma
The syntonic temperament is named after the syntonic comma
, as that is the first comma tempered
to unison in its comma sequence.
Because it has two generators – the octave and tempered perfect fifth (P5) – it is a rank-2
regular temperament. Because one of its generators is the octave, the terminology of Erv Wilson
would describe the syntonic temperament as a linear temperament.
If a two-dimensional arrangement of notes is generated using these same two generators, then it is an isomorphic keyboard
, on which the fingering-pattern of any given musical structure is the same in any syntonic tuning. The combination of an isomorphic keyboard and continuously variable tuning enables Dynamic tonality
, a novel expansion of the framework of tonality.
As shown in the figure at right, the tonally valid tuning range of the syntonic temperament includes a number of historically important tunings, such as the currently popular 12-tone equal division of the octave (12-edo tuning, also known as 12-tone “equal temperament”), the meantone
tunings, and Pythagorean tuning
. Tunings in the syntonic temperament can be equal (12-edo, 31-edo), non-equal (Pythagorean, meantone), circulating, and closely related Just Intonation tunings.
From the center of the syntonic temperament’s tonally valid tuning range, as the width of the P5 widens, the minor second narrows, eventually disappearing in 5-edo where it equals the perfect unison; as the width of the P5 narrows, the minor second widens, eventually equaling the major second in 7-edo.
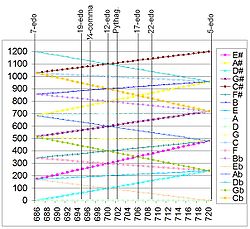 The legend of Figure 2 (on the right side of the figure) shows a stack of P5's centered on D. Each resulting note represents an interval in the syntonic temperament with D as the tonic. The body of the figure shows how the widths (from D) of these intervals change as the width of the P5 is changed across the syntonic temperament's tuning continuum.
The legend of Figure 2 (on the right side of the figure) shows a stack of P5's centered on D. Each resulting note represents an interval in the syntonic temperament with D as the tonic. The body of the figure shows how the widths (from D) of these intervals change as the width of the P5 is changed across the syntonic temperament's tuning continuum.
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
is a product of powers of an octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
and a tempered perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
, with the width of the tempered major third
Major third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
being equal to four tempered perfect fifths minus two octaves and the width of the tempered major second
Major second
In Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions...
being equal to two tempered perfect fifths minus one octave (i.e., half the width of the major third).
Alternatively put, the syntonic temperament:
- generates all non-octave intervals from a stack of temperedMusical temperamentIn musical tuning, a temperament is a system of tuning which slightly compromises the pure intervals of just intonation in order to meet other requirements of the system. Most instruments in modern Western music are tuned in the equal temperament system...
perfect fifths; and - tempers the syntonic commaSyntonic commaIn music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
to unison.
This is the same definition as that of the meantone temperament
Meantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
. The syntonic temperament can be viewed as a systematic extension of the meantone temperament beyond the range imposed by the meantone temperament's need to remain consonant with timbre
Timbre
In music, timbre is the quality of a musical note or sound or tone that distinguishes different types of sound production, such as voices and musical instruments, such as string instruments, wind instruments, and percussion instruments. The physical characteristics of sound that determine the...
s that conform to the harmonic series
Harmonic series (music)
Pitched musical instruments are often based on an approximate harmonic oscillator such as a string or a column of air, which oscillates at numerous frequencies simultaneously. At these resonant frequencies, waves travel in both directions along the string or air column, reinforcing and canceling...
.

Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
, as that is the first comma tempered
Musical temperament
In musical tuning, a temperament is a system of tuning which slightly compromises the pure intervals of just intonation in order to meet other requirements of the system. Most instruments in modern Western music are tuned in the equal temperament system...
to unison in its comma sequence.
Because it has two generators – the octave and tempered perfect fifth (P5) – it is a rank-2
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
regular temperament. Because one of its generators is the octave, the terminology of Erv Wilson
Erv Wilson
Ervin Wilson is a Mexican/American music theorist. Despite his avoidance of academia, Wilson has been influential on those interested in microtonal music and just intonation, especially in the areas of scale, keyboard, and notation design...
would describe the syntonic temperament as a linear temperament.
If a two-dimensional arrangement of notes is generated using these same two generators, then it is an isomorphic keyboard
Isomorphic keyboard
An isomorphic keyboard is a musical input device consisting of a two-dimensional array of note-controlling elements on which any given sequence and/or combination of musical intervals has the “same shape” on the keyboard wherever it occurs – within a key, across keys, across octaves, and across...
, on which the fingering-pattern of any given musical structure is the same in any syntonic tuning. The combination of an isomorphic keyboard and continuously variable tuning enables Dynamic tonality
Dynamic tonality
Dynamic tonality is tonal music which uses real-time changes in tuning and timbre to perform new musical effects such as polyphonic tuning bends, new chord progressions, and temperament modulations, with the option of consonance. The performance of dynamic tonality requires an isomorphic keyboard...
, a novel expansion of the framework of tonality.
As shown in the figure at right, the tonally valid tuning range of the syntonic temperament includes a number of historically important tunings, such as the currently popular 12-tone equal division of the octave (12-edo tuning, also known as 12-tone “equal temperament”), the meantone
Meantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
tunings, and Pythagorean tuning
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
. Tunings in the syntonic temperament can be equal (12-edo, 31-edo), non-equal (Pythagorean, meantone), circulating, and closely related Just Intonation tunings.
From the center of the syntonic temperament’s tonally valid tuning range, as the width of the P5 widens, the minor second narrows, eventually disappearing in 5-edo where it equals the perfect unison; as the width of the P5 narrows, the minor second widens, eventually equaling the major second in 7-edo.

- At P5 ≈ 685.7 cents , the intervals converge on just 7 widths (assuming octave equivalence of 0 and 1200 cents), producing 7-edo.
- At P5 ≈ 694.7 (19-edo), the gaps between these 19 intervals are all equal, producing 19-edo tuning.
- At P5 ≈ 696.8 (31-edo), a stack of 31 such intervals would show equal gaps between each such interval, producing 31-edo tuning.
- At P5 = 700.0 (12-edo), the sharp notes and flat notes are equal, producing 12-edo tuning.
- At P5 ≈ 701.9 (53-edo), a stack of 53 such intervals - each just 3/44 of a cent short of a pure fifth - makes 31 octaves, producing 53-edo tuning.
- etc....
- at P5 = 720.0 cents , the pitches converge on just 5 widths, producing 5-edo.

