In
music theoryMusic theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
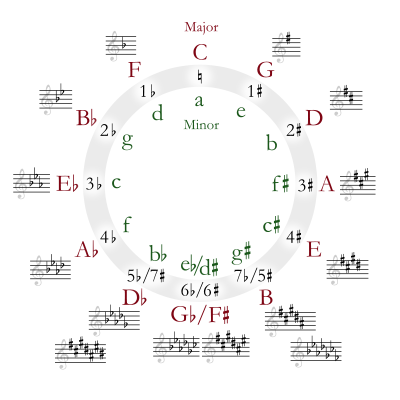
, the
circle of fifths (or
circle of fourths) shows the relationships among the 12 tones of the
chromatic scaleThe chromatic scale is a musical scale with twelve pitches, each a semitone apart. On a modern piano or other equal-tempered instrument, all the half steps are the same size...
, their corresponding
key signatureIn musical notation, a key signature is a series of sharp or flat symbols placed on the staff, designating notes that are to be consistently played one semitone higher or lower than the equivalent natural notes unless otherwise altered with an accidental...
s, and the associated
major and minorIn Western music, the adjectives major and minor can describe a musical composition, movement, section, scale, key, chord, or interval.Major and minor are frequently referred to in the titles of classical compositions, especially in reference to the key of a piece.-Intervals and chords:With regard...
keys. More specifically, it is a
geometricalGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
representation of relationships among the 12
pitch classIn music, a pitch class is a set of all pitches that are a whole number of octaves apart, e.g., the pitch class C consists of the Cs in all octaves...
es of the chromatic scale in
pitch class spaceIn music theory, pitch class space is the circular space representing all the notes in a musical octave.In this space, there is no distinction between tones that are separated by an integral number of octaves...
.
Definition
Since the term 'fifth' defines an interval or mathematical ratio which is the closest and most
consonantIn music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
non-octave interval, then the circle of fifths is a circle of closely related pitches or key tonalities.
MusicianA musician is an artist who plays a musical instrument. It may or may not be the person's profession. Musicians can be classified by their roles in performing music and writing music.Also....* A person who makes music a profession....
s and
composerA composer is a person who creates music, either by musical notation or oral tradition, for interpretation and performance, or through direct manipulation of sonic material through electronic media...
s use the circle of fifths to understand and describe those relationships. The circle's design is helpful in
composingMusical composition can refer to an original piece of music, the structure of a musical piece, or the process of creating a new piece of music. People who practice composition are called composers.- Musical compositions :...
and
harmonizingIn music, harmony is the use of simultaneous pitches , or chords. The study of harmony involves chords and their construction and chord progressions and the principles of connection that govern them. Harmony is often said to refer to the "vertical" aspect of music, as distinguished from melodic...
melodies, building
chordsA chord in music is any harmonic set of two–three or more notes that is heard as if sounding simultaneously. These need not actually be played together: arpeggios and broken chords may for many practical and theoretical purposes be understood as chords...
, and moving to different
keysIn music theory, the term key is used in many different and sometimes contradictory ways. A common use is to speak of music as being "in" a specific key, such as in the key of C major or in the key of F-sharp. Sometimes the terms "major" or "minor" are appended, as in the key of A minor or in the...
within a composition.
At the top of the circle, the
keyIn music theory, the term key is used in many different and sometimes contradictory ways. A common use is to speak of music as being "in" a specific key, such as in the key of C major or in the key of F-sharp. Sometimes the terms "major" or "minor" are appended, as in the key of A minor or in the...
of C Major has no
sharpsIn music, sharp, dièse , or diesis means higher in pitch and the sharp symbol raises a note by a half tone. Intonation may be flat, sharp, or both, successively or simultaneously...
or flats. Starting from the apex and proceeding clockwise by ascending
fifthsIn classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
, the key of G has one sharp, the key of D has 2 sharps, and so on. Similarly, proceeding counterclockwise from the apex by descending fifths, the key of F has one flat, the key of B has 2 flats, and so on. At the bottom of the circle, the sharp and flat keys overlap, showing pairs of
enharmonicIn modern musical notation and tuning, an enharmonic equivalent is a note , interval , or key signature which is equivalent to some other note, interval, or key signature, but "spelled", or named, differently...
key signatures.
Starting at any
pitchPitch is an auditory perceptual property that allows the ordering of sounds on a frequency-related scale.Pitches are compared as "higher" and "lower" in the sense associated with musical melodies,...
, ascending by the interval of an
equal temperedAn equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
fifthIn classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
, one passes all twelve tones clockwise, to return to the beginning pitch class. To pass the twelve tones counterclockwise, it is necessary to ascend by
perfect fourthIn classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
s, rather than fifths. (To the ear, the sequence of fourths gives an impression of settling, or resolution. (see
cadenceIn Western musical theory, a cadence is, "a melodic or harmonic configuration that creates a sense of repose or resolution [finality or pause]." A harmonic cadence is a progression of two chords that concludes a phrase, section, or piece of music...
))
Structure and use
Pitches within the chromatic scale are related not only by the number of semitones between them within the chromatic scale, but also related harmonically within the circle of fifths. Reversing the direction of the circle of fifths gives the
circle of fourths. Typically the "circle of fifths" is used in the analysis of classical music, whereas the "circle of fourths" is used in the analysis of Jazz music, but this distinction is not exclusive. Since fifths and fourths are intervals composed respectively of 7 and 5 semitones, the
circumferenceThe circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
of a circle of fifths is an interval as large as 7 octaves (84 semitones), while the circumference of a circle of fourths equals only 5 octaves (60 semitones).
Diatonic key signatures
The circle is commonly used to represent the relationship between
diatonic scaleIn music theory, a diatonic scale is a seven note, octave-repeating musical scale comprising five whole steps and two half steps for each octave, in which the two half steps are separated from each other by either two or three whole steps...
s. Here, the letters on the circle are taken to represent the major scale with that note as tonic. The numbers on the inside of the circle show how many sharps or flats the
key signatureIn musical notation, a key signature is a series of sharp or flat symbols placed on the staff, designating notes that are to be consistently played one semitone higher or lower than the equivalent natural notes unless otherwise altered with an accidental...
for this scale has. Thus a major scale built on A has 3 sharps in its key signature. The major scale built on F has 1 flat.
For
minor scaleA minor scale in Western music theory includes any scale that contains, in its tonic triad, at least three essential scale degrees: 1) the tonic , 2) a minor-third, or an interval of a minor third above the tonic, and 3) a perfect-fifth, or an interval of a perfect fifth above the tonic, altogether...
s, rotate the letters counter-clockwise by 3, so that, e.g., A minor has 0 sharps or flats and E minor has 1 sharp. (See
relative keyIn music, relative keys are the major and minor scales that have the same key signatures. A major and minor scale sharing the same key signature are said to be in a relative relationship...
for details.) A way to describe this phenomenon is that, for any major key, (i.e. G major, with one sharp in its diatonic scale, F#) a scale can be built beginning on the sixth (VI) degree (relative minor key, in this case, E) containing the same notes, but from E - E as opposed to G - G. Or, G-major scale (G - A - B - C - D - E - F# - G) is enharmonic (harmonically equivalent) to the e-minor scale (E - F# - G - A - B - C - D - E).
Modulation and chord progression
Tonal musicTonality is a system of music in which specific hierarchical pitch relationships are based on a key "center", or tonic. The term tonalité originated with Alexandre-Étienne Choron and was borrowed by François-Joseph Fétis in 1840...
often
modulatesIn music, modulation is most commonly the act or process of changing from one key to another. This may or may not be accompanied by a change in key signature. Modulations articulate or create the structure or form of many pieces, as well as add interest...
by moving between adjacent scales on the circle of fifths. This is because diatonic scales contain seven pitch classes that are contiguous on the circle of fifths. It follows that diatonic scales a perfect fifth apart share six of their seven notes. Furthermore, the notes not held in common differ by only a semitone. Thus modulation by perfect fifth can be accomplished in an exceptionally smooth fashion. For example, to move from the C major scale F – C – G – D – A – E – B to the G major scale C – G – D – A – E – B – F, one need only move the C major scale's "F" to "F".
In Western tonal music, one also finds chord progressions between chords whose roots are related by perfect fifth. For instance, root progressions such as D-G-C are common. For this reason, the circle of fifths can often be used to represent "harmonic distance" between chords.
According to theorists including Goldman,
harmonic functionIn tonal music theory, a diatonic function is the specific, recognized role of each of the 7 notes and their chords in relation to the diatonic key...
(the use, role, and relation of
chordsA chord in music is any harmonic set of two–three or more notes that is heard as if sounding simultaneously. These need not actually be played together: arpeggios and broken chords may for many practical and theoretical purposes be understood as chords...
in
harmonyIn music, harmony is the use of simultaneous pitches , or chords. The study of harmony involves chords and their construction and chord progressions and the principles of connection that govern them. Harmony is often said to refer to the "vertical" aspect of music, as distinguished from melodic...
), including "functional succession", may be "explained by the circle of fifths (in which, therefore, scale degree II is closer to the
dominantIn music, the dominant is the fifth scale degree of the diatonic scale, called "dominant" because it is next in importance to the tonic,and a dominant chord is any chord built upon that pitch, using the notes of the same diatonic scale...
than scale degree IV)". In this view the tonic is considered the end of the line towards which a
chord progressionA chord progression is a series of musical chords, or chord changes that "aims for a definite goal" of establishing a tonality founded on a key, root or tonic chord. In other words, the succession of root relationships...
derived from the circle of fifths progresses.
According to Goldman's
Harmony in Western Music, "the IV chord is actually, in the simplest mechanisms of diatonic relationships, at the greatest distance from I. In terms of the [descending] circle of fifths, it leads away from I, rather than toward it." Thus the progression I-ii-V-I (an authentic cadence) would feel more final or
resolvedResolution in western tonal music theory is the move of a note or chord from dissonance to a consonance .Dissonance, resolution, and suspense can be used to create musical interest...
than I-IV-I (a plagal cadence). Goldman concurs with Nattiez, who argues that "the chord on the fourth degree appears long before the chord on II, and the subsequent final I, in the progression I-IV-vii
o-iii-vi-ii-V-I", and is farther from the tonic there as well. (In this and related articles, upper-case Roman numerals indicate major triads while lower-case Roman numerals indicate minor triads.)
Goldman argues that "historically the use of the IV chord in harmonic design, and especially in
cadencesIn Western musical theory, a cadence is, "a melodic or harmonic configuration that creates a sense of repose or resolution [finality or pause]." A harmonic cadence is a progression of two chords that concludes a phrase, section, or piece of music...
, exhibits some curious features. By and large, one can say that the use of IV in final cadences becomes more common in the nineteenth century than it was in the eighteenth, but that it may also be understood as a substitute for the ii chord when it precedes V. It may also be quite logically construed as an incomplete ii7 chord (lacking root)." The delayed acceptance of the IV-I in final cadences is explained aesthetically by its lack of closure, caused by its position in the circle of fifths. The earlier use of IV-V-I is explained by proposing a relation between IV and ii, allowing IV to substitute for or serve as ii. However, Nattiez calls this latter argument "a narrow escape: only the theory of a ii chord without a
rootIn music theory, the root of a chord is the note or pitch upon which a triadic chord is built. For example, the root of the major triad C-E-G is C....
allows Goldman to maintain that the circle of fifths is completely valid from
BachJohann Sebastian Bach was a German composer, organist, harpsichordist, violist, and violinist whose sacred and secular works for choir, orchestra, and solo instruments drew together the strands of the Baroque period and brought it to its ultimate maturity...
to
WagnerWilhelm Richard Wagner was a German composer, conductor, theatre director, philosopher, music theorist, poet, essayist and writer primarily known for his operas...
", or the entire
common practice periodThe common practice period, in the history of Western art music , spanning the Baroque, Classical, and Romantic periods, lasted from c. 1600 to c. 1900.-General characteristics:...
.
Circle closure in non-equal tuning systems
When an instrument is tuned with the
equal temperamentAn equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
system, the width of the fifths is such that the circle "closes". This means that ascending by twelve fifths from any pitch, one returns to a tune exactly in the same pitch class as the initial tune, and exactly seven
octaveIn music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
s above it. To obtain such a perfect circle closure, the fifth is slightly flattened with respect to its
just intonationIn music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
(3:2
interval ratioIn music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth is 3:2 , 1.5, and may be approximated by an equal tempered perfect fifth which is 27/12, 1.498...
).
Thus, ascending by justly intonated fifths fails to close the circle by an excess of approximately 23.46
centsThe cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...
, roughly a quarter of a
semitoneA semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
, an interval known as the
Pythagorean commaIn musical tuning, the Pythagorean comma , named after the ancient mathematician and philosopher Pythagoras, is the small interval existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B , or D and C...
. In Pythagorean tuning, this problem is solved by markedly shortening the
widthIn music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
of one of the twelve fifths, which makes it severely
dissonantIn music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
. This anomalous fifth is called wolf fifth as a humorous metaphor of the unpleasant sound of the note (like a wolf trying to howl an off-pitch note). The
quarter-comma meantoneQuarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning...
tuning system uses eleven fifths slightly narrower than the equally tempered fifth, and requires a much wider and even more dissonant wolf fifth to close the circle. More complex tuning systems based on
just intonationIn music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
, such as 5-limit tuning, use at most eight justly tuned fifths and at least three non-just fifths (some slightly narrower, and some slightly wider than the just fifth) to close the circle.
In lay terms
A simple way to see the
musical intervalIn music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
known as a
fifthIn classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
is by looking at a
piano keyboardA musical keyboard is the set of adjacent depressible levers or keys on a musical instrument, particularly the piano. Keyboards typically contain keys for playing the twelve notes of the Western musical scale, with a combination of larger, longer keys and smaller, shorter keys that repeats at the...
, and, starting at any key, counting seven keys to the right (both black and white) to get to the next note on the circle shown above. Seven half steps, the distance from the 1st to the 8th key on a piano is a "perfect fifth", called 'perfect' because it is neither major nor minor, but applies to both major and minor scales and chords, and a 'fifth' because though it is a distance of seven semitones on a keyboard, it is a distance of five steps within a major or minor scale.
A simple way to hear the relationship between these notes is by playing them on a piano keyboard. If you traverse the circle of fifths backwards, the notes will feel as though they fall into each other. This aural relationship is what the mathematics describes.
Perfect fifths may be
justly tunedIn music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
or
temperedIn musical tuning, a temperament is a system of tuning which slightly compromises the pure intervals of just intonation in order to meet other requirements of the system. Most instruments in modern Western music are tuned in the equal temperament system...
. Two notes whose frequencies differ by a ratio of 3:2 make the interval known as a justly tuned perfect fifth. Cascading twelve such fifths does not return to the original
pitch classIn music, a pitch class is a set of all pitches that are a whole number of octaves apart, e.g., the pitch class C consists of the Cs in all octaves...
after going round the circle, so the 3:2 ratio may be slightly detuned, or tempered. Temperament allows perfect fifths to cycle, and allows pieces to be
transposedIn music transposition refers to the process, or operation, of moving a collection of notes up or down in pitch by a constant interval.For example, one might transpose an entire piece of music into another key...
, or played in any
keyIn music theory, the term key is used in many different and sometimes contradictory ways. A common use is to speak of music as being "in" a specific key, such as in the key of C major or in the key of F-sharp. Sometimes the terms "major" or "minor" are appended, as in the key of A minor or in the...
on a piano or other fixed-pitch instrument without distorting their harmony. The primary tuning system used for Western (especially
keyboardA keyboard instrument is a musical instrument which is played using a musical keyboard. The most common of these is the piano. Other widely used keyboard instruments include organs of various types as well as other mechanical, electromechanical and electronic instruments...
and
fretA fret is a raised portion on the neck of a stringed instrument, that extends generally across the full width of the neck. On most modern western instruments, frets are metal strips inserted into the fingerboard...
ted) instruments today is called twelve-tone
equal temperamentAn equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
.
History
In 1679 a
treatiseA treatise is a formal and systematic written discourse on some subject, generally longer and treating it in greater depth than an essay, and more concerned with investigating or exposing the principles of the subject.-Noteworthy treatises:...
called Grammatika was written by the composer and theorist Nikolai Diletskii. Diletskii’s Grammatika is a treatise on composition, the first of its kind, which targeted Western-style polyphonic compositions. It taught how to write kontserty, polyphonic
a cappellaA cappella music is specifically solo or group singing without instrumental sound, or a piece intended to be performed in this way. It is the opposite of cantata, which is accompanied singing. A cappella was originally intended to differentiate between Renaissance polyphony and Baroque concertato...
, which were normally based on liturgical texts and were created by putting together musical sections that have contrasting
rhythmRhythm may be generally defined as a "movement marked by the regulated succession of strong and weak elements, or of opposite or different conditions." This general meaning of regular recurrence or pattern in time may be applied to a wide variety of cyclical natural phenomena having a periodicity or...
, meters, melodic material and vocal groupings. Diletskii intended his treatise to be a guide to composition but pertaining to the rules of
music theoryMusic theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
. Within the Grammatika treatise is where the first circle of fifths appeared and was used for students as a composer's tool. Using the circle of fifths Diletskii showed how a series of musical ideas could be expanded by the use of similar letters.
Diatonic circle of fifths
The diatonic circle of fifths is the circle of fifths encompassing only members of the diatonic scale. As such, it contains a diminished fifth, in C major between B and F. See
structure implies multiplicityIn diatonic set theory structure implies multiplicity is a quality of a collection or scale. This is that for the interval series formed by the shortest distance around a diatonic circle of fifths between member of a series indicates the number of unique interval patterns formed by diatonic...
.
The
circle progressionIn music, the circle progression is a chord progression named for the circle of fifths, along which it travels. It is "undoubtedly the most common and the strongest of all harmonic progressions" and consists of "adjacent roots in ascending fourth or descending fifth relationship", with movement by...
is commonly a circle through the diatonic chords by fifths, including one
diminished chordA diminished triad chord or diminished chord is a triad consisting of two minor thirds above the root — if built on C, a diminished chord would have a C, an E and a G. It resembles a minor triad with a lowered fifth....
and one progression by diminished fifth:
Chromatic circle
The circle of fifths is closely related to the
chromatic circleThe chromatic circle is a geometrical space that shows relationships among the 12 equal-tempered pitch classes making up the familiar chromatic scale...
, which also arranges the twelve equal-tempered pitch classes in a circular ordering. A key difference between the two circles is that the
chromatic circleThe chromatic circle is a geometrical space that shows relationships among the 12 equal-tempered pitch classes making up the familiar chromatic scale...
can be understood as a continuous space where every point on the circle corresponds to a conceivable
pitch classIn music, a pitch class is a set of all pitches that are a whole number of octaves apart, e.g., the pitch class C consists of the Cs in all octaves...
, and every conceivable pitch class corresponds to a point on the circle. By contrast, the circle of fifths is fundamentally a
discrete structure, and there is no obvious way to assign pitch classes to each of its points. In this sense, the two circles are mathematically quite different.
However, the twelve equal-tempered
pitch classIn music, a pitch class is a set of all pitches that are a whole number of octaves apart, e.g., the pitch class C consists of the Cs in all octaves...
es can be represented by the
cyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order twelve, or equivalently, the
residue classesIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
modulo twelve,
. The group
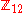has four generators, which can be identified with the ascending and descending semitones and the ascending and descending perfect fifths. The semitonal generator gives rise to the
chromatic circleThe chromatic circle is a geometrical space that shows relationships among the 12 equal-tempered pitch classes making up the familiar chromatic scale...
while the perfect fifth gives rise to the circle of fifths.
Relation with chromatic scale
The circle of fifths, or fourths, may be mapped from the
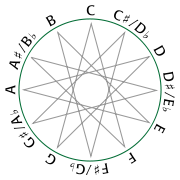
chromatic scaleThe chromatic scale is a musical scale with twelve pitches, each a semitone apart. On a modern piano or other equal-tempered instrument, all the half steps are the same size...
by
multiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, and vice versa. To map between the circle of fifths and the chromatic scale (in integer notation) multiply by 7 (
M7Twelve-tone technique is a method of musical composition devised by Arnold Schoenberg...
), and for the circle of fourths multiply by 5 (P5).
Here is a demonstration of this procedure. Start off with an
orderedOrder theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
12-tuple (
tone rowIn music, a tone row or note row , also series and set, refers to a non-repetitive ordering of a set of pitch-classes, typically of the twelve notes in musical set theory of the chromatic scale, though both larger and smaller sets are sometimes found.-History and usage:Tone rows are the basis of...
) of integers
- (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)
representing the notes of the chromatic scale: 0 = C, 2 = D, 4 = E, 5 = F, 7 = G, 9 = A, 11 = B, 1 = C, 3 = D, 6 = F, 8 = G, 10 = A. Now multiply the entire 12-tuple by 7:
- (0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77)
and then apply a
moduloIn computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
12 reduction to each of the numbers (subtract 12 from each number as many times as necessary until the number becomes smaller than 12):
- (0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5)
which is equivalent to
- (C, G, D, A, E, B, F, C, G, D, A, F)
which is the circle of fifths.
Note that this is
enharmonicIn modern musical notation and tuning, an enharmonic equivalent is a note , interval , or key signature which is equivalent to some other note, interval, or key signature, but "spelled", or named, differently...
ally equivalent to:
- (C, G, D, A, E, B, G, D, A, E, B, F)
Enharmonics
The “bottom keys” of the circle of fifths are often written in flats and sharps, as they are easily interchanged using enharmonics. For example, the key of B, with five sharps, is enharmonically equivalent to the key of C, with 7 flats. But the circle of fifths doesn’t stop at 7 sharps (C) or 7 flats (C). Following the same pattern, one can construct a circle of fifths with all sharp keys, or all flat keys.
After C comes the key of G (following the pattern of being a fifth higher, and, coincidentally, enharmonically equivalent to the key of A). The “8th sharp” is placed on the F, to make it F. The key of D, with 9 sharps, has another sharp placed on the C, making it C. The same for key signatures with flats is true; The key of E (four sharps) is equivalent to the key of F (again, one fifth below the key of C, following the pattern of flat key signatures. The last flat is placed on the B, making it B.)
See also
- Approach chord
In music, an approach chord is a chord one half-step higher or lower than the goal, especially in the context of turnarounds and cycle-of-fourths progressions, for example the two bar 50s progression: |G Em |Am D7 ||may be filled in with approach chords: |G F9 Em Abm |Am D#7 D7 Gb7...
- Array system
- Sonata form
Sonata form is a large-scale musical structure used widely since the middle of the 18th century . While it is typically used in the first movement of multi-movement pieces, it is sometimes used in subsequent movements as well—particularly the final movement...
- Well temperament
Well temperament is a type of tempered tuning described in 20th-century music theory. The term is modelled on the German word wohltemperiert which appears in the title of J.S. Bach's famous composition, The Well-Tempered Clavier...
- Circle of fifths text table
The Circle of fifths, text table, shows the number of flats or sharps in each of the diatonic musical scales and keys. Both C major and A minor keys have no flats or sharps....
Further reading
- Lester, Joel. Between Modes and Keys: German Theory, 1592–1802. 1990.
- Miller, Michael. The Complete Idiot's Guide to Music Theory, 2nd ed. [Indianapolis, IN]: Alpha, 2005. ISBN 1592574378.
- Purwins, Hendrik (2005)."Profiles of Pitch Classes: Circularity of Relative Pitch and Key—Experiments, Models, Computational Music Analysis, and Perspectives". Ph.D. Thesis. Berlin: Technische Universität Berlin.
- Purwins, Hendrik, Benjamin Blankertz, and Klaus Obermayer (2007). " Toroidal Models in Tonal Theory and Pitch-Class Analysis". in: . Computing in Musicology 15 ("Tonal Theory for the Digital Age"): 73–98.
External links