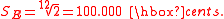Five-limit tuning
Encyclopedia
Five-limit tuning, or 5-limit tuning is a method to obtain a justly tuned
musical scale
. The frequencies of the notes of such a scale are obtained by multiplying the frequency of a given reference note (the base note) by powers
of 2, 3, or 5, or a combination of them. For instance, if the base note is C and its frequency is fC, the frequency of E is

In other words, the ratio between the two frequencies (interval ratio
) is:
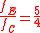
This implies that the tones defined by this system are regular number
harmonic
s of a single fundamental frequency
.
or chromatic scale
in just intonation in many ways, all of which make certain chords purely tuned and as consonant and stable as possible, and the other chords not accommodated and considerably less stable.
The prominent notes of a given scale are tuned so that their frequencies form ratios of relatively small integers. For example, in the key of G major
, the ratio of the frequencies of the notes G to D (a perfect fifth
) is 3/2, while that of G to C (a perfect fourth
) is 4/3. Three basic intervals can be used to construct any interval involving the prime numbers 2, 3, and 5 (known as 5-limit just intonation):
which combine to form:
A just diatonic scale may be derived as follows. Suppose we insist that the chords FAC, CEG, and GBD be just major triads
(then ACE and EGB are just minor triads
, but DFA is not; see syntonic comma
).
Then we obtain this scale:
The major thirds are correct, and two minor thirds are right, and D to F is a semiditone or Pythagorean minor third (equal to three just perfect fifths, descending), a syntonic comma narrower than a justly tuned third. Concerning triads, the triads on I, IV, and V are 4:5:6, the triad on ii is 27:32:40, the triads on iii and vi are 10:12:15, and the triad on vii is 45:54:64.
Another way to do it is as follows. We can insist that the chords DFA, ACE, and EGB
be just minor triads
(then FAC and CEG are just major triads
, but GBD is not).
Then we get the following scale:
The minor thirds are correct, and two major thirds are right, but B to D is not.
If we compare with the scale above, we see that six notes can be lined up, but one note, D, has changed its value. It is evidently not possible to get all six chords mentioned correct.
There are other possibilities; instead of lowering D, we can raise A. But this breaks something else.
The factors listed in the first row and column are powers of 3 and 5, respectively (e.g., 1/9 = 3-2). Colors indicate couples of enharmonic
notes with almost identical pitch. The ratios are all expressed relative to C in the centre of this diagram (the base note for this scale). They are computed in two steps:
Note that the powers of 2 used in the second step may be interpreted as ascending or descending octave
s. For instance, multiplying the frequency of a note by 25 means increasing it by 5 octaves. Moreover, each row of the table may be considered to be a sequence of fifths
(ascending to the right), and each column a sequence of major third
s (ascending upward). For instance, in the first row of the table, there is an ascending fifth from D and A, and another one (followed by a descending octave) from A to E. This suggests an alternative but equivalent method for computing the same ratios. For instance, you can obtain A (5/3 ratio), starting from C, by moving one cell to the left and one upward in the table, which means descending by one fifth (2/3) and ascending by one major third (5/4):
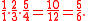
Since this is below C, you need to move up by an octave to end up within the desired range of ratios (from 1/1 to 2/1):

A 12 tone scale is obtained by removing one note for each couple of enharmonic notes. This can be done in at least three ways, which have in common the removal of G, according to a convention which was valid even for C-based Pythagorean and 1/4-comma meantone scales. The first strategy, which we operationally denote here as symmetric scale 1, consists of selecting for removal the tones in the upper left and lower right corners of the table. The second one, denoted as symmetric scale 2, consists of discarding the notes in the first and last cell of the second row (labeled "1"). The third one, denoted as asymmetric scale, consists of discarding the first column (labeled "1/9"). The resulting 12-tone scales are shown below:
In the first and second scale, B and D are exactly the inversion of each other. This is not true for the third one. This is the reason why these two scales are regarded as symmetric (although the removal of G makes all 12 tone scales, including those produced with any other tuning system, slightly asymmetric).
The asymmetric system has the advantage of having the "justest" ratios (those containing smaller numbers), nine pure fifths (factor 3/2), eight pure major thirds (factor 5/4) by design, but also six pure minor third
s (factor 6/5). It contains however also many intervals that are less pure (e.g. D to A is 40/27 rather than 3/2), which practically limits modulation
to a narrow range of keys. The chords of the tonic C, dominant G and subdominant F are pure, as well as D, A, E and the minor chords Fm, Cm, Gm, Am, Bm and Em, but not the Dm.
A drawback of the asymmetric system is that it produces 14 wolf intervals, rather than 12 as for the symmetric ones (see below).
The B in the first symmetric scale differs from the B in the other scales by the syntonic comma
, being over 21 cents. In equally tempered scales, the difference is eliminated by making all steps the same frequency ratio.
The construction of the asymmetric scale is graphically shown in the picture. Each block has the height in cents of the constructive frequency ratios 2, 3 and 5. Recurring patterns can be recognised. For example, many times the next note is created by replacing a 5-block and a 3-block by four 2-blocks in the full picture and one in the simplified, or a ratio of 16/15.
For a similar image, where using frequency factors 2/1, 3/2, and 5/4, rather than 2, 3, and 5, see here.
of intervals in other scales (for instance, see this comparison table). However, 5-limit tuning is not the only method to obtain just intonation
. It is possible to construct just intervals with even "juster" ratios, or with values closer to the equal-tempered equivalents. For instance, a 7-limit tuning is sometimes used to obtain a slightly juster and consequently more consonant interval for the minor seventh (7/4) and its inversion, the major second (8/7). A list of these reference ratios, which may be referred to as pure or strictly just intervals or ratios, is provided below:
Cells highlighted in yellow indicate intervals that are juster than those in the non-coloured cells in the same row. Those highlighted in cyan indicate even juster ratios. The symmetric scale 2 has not been shown because it is a solution equivalent to the symmetric scale 1 (with respect to which has one juster and one less just interval) and is not frequently used for comparisons.
Notice that the ratios 45/32 and 64/45 for the tritone
s (augmented fourth and diminished fifth) are not in all contexts regarded as strictly just, but they are the justest possible in the above mentioned 5-limit tuning scales. An extended asymmetric 5-limit scale (see below) provides slightly juster ratios for both the tritones (25/18 and 36/25), the purity of which is also controversial. 7-limit tuning allows for the justest possible ratios, namely 7/5 (about 582.512 cents, also known as septimal tritone
) and 10/7 (about 617.488 cents). These ratios are more consonant than 17/12 (about 603.000 cents) and 24/17 (about 597.000 cents), which can be obtained in 17-limit tuning, yet the latter are also fairly common, as they are closer to the equal-tempered value of 600.000 cents.
The above mentioned 7/4 interval (about 968.826 cents), also known as the septimal minor seventh, or harmonic seventh, has been a contentious issue throughout the history of music theory; it is 31 cents flatter than an equal-tempered minor seventh. Some assert the 7/4 is one of the blue note
s used in jazz
.
s, twelve intervals composed of 2 semitones, twelve intervals composed of 3 semitones, etc.).
In 5-limit tuning, each of the interval types, except for the unisons and the octaves, has three or even four different sizes. This is the price paid for seeking just intonation. The tables on the right and below show their frequency ratios and their approximate sizes in cents, for the "asymmetric scale". Similar tables, for the "symmetric scale 1", are published here and here. Interval names are given in their standard shortened form. For instance, the size of the interval from C to G, which is a perfect fifth (P5), can be found in the seventh column of the row labeled C. Pure intervals, as defined above, are shown in bold font (notice that, as explained above, the justly intonated ratio 45/32 ≈ 590 cents, for A4, is not considered to be pure).
A color code is used to distinguish the intervals which deviate from the reference sizes shown in the construction table, and to show the amount of their deviation. Wolf intervals are marked in black.
The reason why the interval sizes vary throughout the scale is that the pitches forming the scale are unevenly spaced. Namely, the frequencies defined by construction for the twelve notes determine four different semitone
s (i.e. intervals between adjacent notes). For instance:
Conversely, in an equally tempered chromatic scale, by definition the twelve pitches are equally spaced, all semitones having a size of exactly
As a consequence all intervals of any given type have the same size (e.g., all major thirds have the same size, all fifths have the same size, etc.). The price paid, in this case, is that none of them is justly tuned and perfectly consonant, except, of course, for the unison and the octave.
Note that 5-limit tuning was designed to maximize the number of pure intervals, but even in this system several intervals are markedly impure (for instance, as shown in the figures, 60 out of 144 intervals deviate by at least 19.6 cents from the justly intonated reference sizes shown in the construction table). Also, 5-limit tuning yields a much larger number of wolf intervals with respect to Pythagorean tuning, which can be considered a 3-limit just intonation tuning. Namely, while Pythagorean tuning determines only 2 wolf intervals (a fifth and a fourth), the 5-limit symmetric scales produce 12 of them, and the asymmetric scale 14. It is also important to note that the two fifths, three minor thirds, and three major sixths marked in orange in the tables (ratio 40/27, 32/27, and 27/16 (or G−, E−, and A+), even though they do not completely meet the conditions to be regarded as wolf intervals, deviate from the corresponding pure ratio by an amount (1 syntonic comma
, i.e. 81/80, or about 21.5 cents) large enough to be clearly perceived as dissonant
.
Clearly, the more we try to increase the number of pure and consonant
intervals, the more the remaining ones become impure and dissonant, by compensation. Some of the major seconds (M2) and minor sevenths (m7) represent the only exception to this rule. As you can see in the tables, those marked in orange are pure (10/9 and 16/9), even if their size is 81/80 narrower than the corresponding reference size (9/8 and 9/5).
For a comparison with other tuning systems, see also this table.
may be defined as a minute interval, equal to the difference between two kinds of semitone
s (diatonic and chromatic, also known as minor second, m2, or augmented unison, A1). In this case, however, 4 different kinds of semitones are produced (two A1, S1 and S2, and two m2, S3 and S4), and 12 different commas can be defined as the differences between their sizes in cents, or equivalently as the ratios between their ratios. Among these, we select the six ascending ones (those with ratio larger than 1/1, and positive size in cents):
The other six ratios are discarded because they are just the opposite of these, and hence they have exactly the same length, but an opposite direction (i.e. a descending direction, a ratio smaller than 1/1, and a negative size in cents). We obtain commas of four different sizes: the diaschisma, the lesser diesis, the syntonic comma, and the greater diesis. Since S1 (the just A1) and S3 (the just m2) are the most often occurring semitones in this 12-tone scale (see tables above), the lesser diesis, being defined as the ratio between them, is the most often observed comma.
The syntonic comma is also defined, in 5-limit tuning, as the ratio between the major tone
(M2 with size 9/8) and the minor tone (M2 with size 10/9). Notice that it cannot be defined, in other tuning systems, as the ratio between diatonic and cromatic semitones (m2/A1), but it is an important reference value used to tune the perfect fifth
in any tuning system in the syntonic temperament
continuum (including also meantone temperaments).
, being the difference between the sizes in cents of a diatonic and a chromatic semitone (or equivalently the ratio between their frequency ratios).
On the contrary, the syntonic comma is defined either as the difference in cents between two chromatic semitones (S2 and S1), or between two diatonic semitones (S4 and S3), and cannot be considered to be a diminished second.
For instance, one can obtain 35 pitches by adding rows in each direction like this:
The left column (1/9) is sometimes removed (as in the asymmetric scale shown above), thus creating an asymmetric table with a smaller number of pitches. Notice that a juster ratio is produced for the diminished fifth (C-G = 36/25), with respect to the restricted 5-limit tuning described above (where C to G-
= 64/45).
and its inversion, the perfect fourth
. The Pythagorean major third
(81:64) and minor third
(32:27) were dissonant
, and this prevented musicians from using triad
s and chord
s, forcing them for centuries to write music with relatively simple texture
. In late Middle Ages
, musicians realized that by slightly tempering the pitch of some notes, the Pythagorean thirds could be made consonant
. For instance, if you decrease by a syntonic comma
(81:80) the frequency of E, C-E (a major third), and E-G (a minor third) become just. Namely, C-E is flattened to a justly intonated ratio of

and at the same time E-G is sharpened to the just ratio of
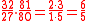
The drawback is that the fifths A-E and E-B, by flattening E, become almost as dissonant as the Pythagorean wolf fifth
. But the fifth C-G stays consonant, since only E has been flattened (C-E * E-G = 5/4 * 6/5 = 3/2), and can be used together with C-E to produce a C-major
triad (C-E-G).
By generalizing this simple rationale, Gioseffo Zarlino
, in the late sixteenth century, created the first justly intonated 7-tone (diatonic
) scale, which contained pure perfect fifths (3:2), pure major thirds, and pure minor thirds:
F → A → C → E → G → B → D
This is a sequence of just major thirds (M3, ratio 5:4) and just minor thirds (m3, ratio 6:5), starting from F:
F + M3 + m3 + M3 + m3 + M3 + m3
Since M3 + m3 = P5 (perfect fifth), i.e. 5/4 * 6/5 = 3/2, this is exactly equivalent to the diatonic scale obtained in 5-limit just intonation, and hence can be viewed as a subset of the construction table used for the 12-tone (chromatic
) scale:
where both rows are sequences of just fifths, and F-A, C-E, G-B are just major thirds:
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
musical scale
Musical scale
In music, a scale is a sequence of musical notes in ascending and descending order. Most commonly, especially in the context of the common practice period, the notes of a scale will belong to a single key, thus providing material for or being used to conveniently represent part or all of a musical...
. The frequencies of the notes of such a scale are obtained by multiplying the frequency of a given reference note (the base note) by powers
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of 2, 3, or 5, or a combination of them. For instance, if the base note is C and its frequency is fC, the frequency of E is

In other words, the ratio between the two frequencies (interval ratio
Interval ratio
In music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth is 3:2 , 1.5, and may be approximated by an equal tempered perfect fifth which is 27/12, 1.498...
) is:
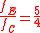
This implies that the tones defined by this system are regular number
Regular number
Regular numbers are numbers that evenly divide powers of 60. As an example, 602 = 3600 = 48 × 75, so both 48 and 75 are divisors of a power of 60...
harmonic
Harmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
s of a single fundamental frequency
Fundamental frequency
The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the lowest frequency of a periodic waveform. In terms of a superposition of sinusoids The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the...
.
Diatonic scale
It is possible to tune the familiar diatonic scaleDiatonic scale
In music theory, a diatonic scale is a seven note, octave-repeating musical scale comprising five whole steps and two half steps for each octave, in which the two half steps are separated from each other by either two or three whole steps...
or chromatic scale
Chromatic scale
The chromatic scale is a musical scale with twelve pitches, each a semitone apart. On a modern piano or other equal-tempered instrument, all the half steps are the same size...
in just intonation in many ways, all of which make certain chords purely tuned and as consonant and stable as possible, and the other chords not accommodated and considerably less stable.
The prominent notes of a given scale are tuned so that their frequencies form ratios of relatively small integers. For example, in the key of G major
G major
G major is a major scale based on G, with the pitches G, A, B, C, D, E, and F. Its key signature has one sharp, F; in treble-clef key signatures, the sharp-symbol for F is usually placed on the first line from the top, though in some Baroque music it is placed on the first space from the bottom...
, the ratio of the frequencies of the notes G to D (a perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
) is 3/2, while that of G to C (a perfect fourth
Perfect fourth
In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
) is 4/3. Three basic intervals can be used to construct any interval involving the prime numbers 2, 3, and 5 (known as 5-limit just intonation):
- s = 16:15 (SemitoneSemitoneA semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
) - t = 10:9 (Minor tone)
- T = 9:8 (Major tone)
which combine to form:
- 6:5 = Ts (minor third)
- 5:4 = Tt (major third)
- 4:3 = Tts (perfect fourth)
- 3:2 = TTts (perfect fifth)
- 2:1 = TTTttss (octave)
A just diatonic scale may be derived as follows. Suppose we insist that the chords FAC, CEG, and GBD be just major triads
Major chord
In music theory, a major chord is a chord having a root, a major third, and a perfect fifth. When a chord has these three notes alone, it is called a major triad...
(then ACE and EGB are just minor triads
Minor chord
In music theory, a minor chord is a chord having a root, a minor third, and a perfect fifth.When a chord has these three notes alone, it is called a minor triad....
, but DFA is not; see syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
).
Then we obtain this scale:
| Note | Name | C | D | E | F | G | A | B | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 | |||||||||
| Natural | 24 | 27 | 30 | 32 | 36 | 40 | 45 | 48 | |||||||||
| Cents | 0 | 204 | 386 | 498 | 702 | 884 | 1088 | 1200 | |||||||||
| Step | Name | T | t | s | T | t | T | s | |||||||||
| Ratio | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 | ||||||||||
| Cents | 204 | 182 | 112 | 204 | 182 | 204 | 112 | ||||||||||
The major thirds are correct, and two minor thirds are right, and D to F is a semiditone or Pythagorean minor third (equal to three just perfect fifths, descending), a syntonic comma narrower than a justly tuned third. Concerning triads, the triads on I, IV, and V are 4:5:6, the triad on ii is 27:32:40, the triads on iii and vi are 10:12:15, and the triad on vii is 45:54:64.
Another way to do it is as follows. We can insist that the chords DFA, ACE, and EGB
be just minor triads
Minor chord
In music theory, a minor chord is a chord having a root, a minor third, and a perfect fifth.When a chord has these three notes alone, it is called a minor triad....
(then FAC and CEG are just major triads
Major chord
In music theory, a major chord is a chord having a root, a major third, and a perfect fifth. When a chord has these three notes alone, it is called a major triad...
, but GBD is not).
Then we get the following scale:
| Note | A | B | C | D | E | F | G | A | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 9/8 | 6/5 | 4/3 | 3/2 | 8/5 | 9/5 | 2/1 | ||||||||
| Natural | 120 | 135 | 144 | 160 | 180 | 192 | 216 | 240 | ||||||||
| Cents | 0 | 204 | 316 | 498 | 702 | 814 | 1018 | 1200 | ||||||||
| Step | T | s | t | T | s | T | t | |||||||||
| Cent step | 204 | 112 | 182 | 204 | 112 | 204 | 182 | |||||||||
The minor thirds are correct, and two major thirds are right, but B to D is not.
If we compare with the scale above, we see that six notes can be lined up, but one note, D, has changed its value. It is evidently not possible to get all six chords mentioned correct.
There are other possibilities; instead of lowering D, we can raise A. But this breaks something else.
Twelve tone scale
To build a twelve tone scale in 5-limit tuning, we start by constructing a table containing fifteen justly intonated pitches:| Factor | 1/9 | 1/3 | 1 | 3 | 9 | |
|---|---|---|---|---|---|---|
| 5 | note ratio cents |
D− 10/9 182 |
A 5/3 884 |
E 5/4 386 |
B 15/8 1088 |
F+ 45/32 590 |
| 1 | note ratio cents |
B− 16/9 996 |
F 4/3 498 |
C 1 0 |
G 3/2 702 |
D 9/8 204 |
| 1/5 | note ratio cents |
G− 64/45 610 |
D− 16/15 112 |
A 8/5 814 |
E 6/5 316 |
B 9/5 1018 |
The factors listed in the first row and column are powers of 3 and 5, respectively (e.g., 1/9 = 3-2). Colors indicate couples of enharmonic
Enharmonic
In modern musical notation and tuning, an enharmonic equivalent is a note , interval , or key signature which is equivalent to some other note, interval, or key signature, but "spelled", or named, differently...
notes with almost identical pitch. The ratios are all expressed relative to C in the centre of this diagram (the base note for this scale). They are computed in two steps:
- For each cell of the table, a base ratio is obtained by multiplying the corresponding factors. For instance, the base ratio for the lower-left cell is 1/9 · 1/5 = 1/45.
- The base ratio is then multiplied by a negative or positive power of 2, as large as needed to bring it within the range of the octave starting from C (from 1/1 to 2/1). For instance, the base ratio for the lower left cell (1/45) is multiplied by 25, and the resulting ratio is 64/45, which is a number between 1/1 and 2/1.
Note that the powers of 2 used in the second step may be interpreted as ascending or descending octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
s. For instance, multiplying the frequency of a note by 25 means increasing it by 5 octaves. Moreover, each row of the table may be considered to be a sequence of fifths
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
(ascending to the right), and each column a sequence of major third
Major third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
s (ascending upward). For instance, in the first row of the table, there is an ascending fifth from D and A, and another one (followed by a descending octave) from A to E. This suggests an alternative but equivalent method for computing the same ratios. For instance, you can obtain A (5/3 ratio), starting from C, by moving one cell to the left and one upward in the table, which means descending by one fifth (2/3) and ascending by one major third (5/4):
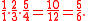
Since this is below C, you need to move up by an octave to end up within the desired range of ratios (from 1/1 to 2/1):

A 12 tone scale is obtained by removing one note for each couple of enharmonic notes. This can be done in at least three ways, which have in common the removal of G, according to a convention which was valid even for C-based Pythagorean and 1/4-comma meantone scales. The first strategy, which we operationally denote here as symmetric scale 1, consists of selecting for removal the tones in the upper left and lower right corners of the table. The second one, denoted as symmetric scale 2, consists of discarding the notes in the first and last cell of the second row (labeled "1"). The third one, denoted as asymmetric scale, consists of discarding the first column (labeled "1/9"). The resulting 12-tone scales are shown below:
| Symmetric scale 1 | |||||
|---|---|---|---|---|---|
| Factor | 1/9 | 1/3 | 1 | 3 | 9 |
| 5 | A 5/3 |
E 5/4 |
B 15/8 |
F+ 45/32 |
|
| 1 | B− 16/9 |
F 4/3 |
C 1 |
G 3/2 |
D 9/8 |
| 1/5 | D− 16/15 |
A 8/5 |
E 6/5 |
| Symmetric scale 2 | |||||
|---|---|---|---|---|---|
| Factor | 1/9 | 1/3 | 1 | 3 | 9 |
| 5 | D− 10/9 |
A 5/3 |
E 5/4 |
B 15/8 |
F+ 45/32 |
| 1 | F 4/3 |
C 1 |
G 3/2 |
||
| 1/5 | D− 16/15 |
A 8/5 |
E 6/5 |
B 9/5 |
| Asymmetric scale | |||||
|---|---|---|---|---|---|
| Factor | 1/9 | 1/3 | 1 | 3 | 9 |
| 5 | A 5/3 |
E 5/4 |
B 15/8 |
F+ 45/32 |
|
| 1 | F 4/3 |
C 1 |
G 3/2 |
D 9/8 |
|
| 1/5 | D− 16/15 |
A 8/5 |
E 6/5 |
B 9/5 |
In the first and second scale, B and D are exactly the inversion of each other. This is not true for the third one. This is the reason why these two scales are regarded as symmetric (although the removal of G makes all 12 tone scales, including those produced with any other tuning system, slightly asymmetric).
The asymmetric system has the advantage of having the "justest" ratios (those containing smaller numbers), nine pure fifths (factor 3/2), eight pure major thirds (factor 5/4) by design, but also six pure minor third
Minor third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major...
s (factor 6/5). It contains however also many intervals that are less pure (e.g. D to A is 40/27 rather than 3/2), which practically limits modulation
Modulation (music)
In music, modulation is most commonly the act or process of changing from one key to another. This may or may not be accompanied by a change in key signature. Modulations articulate or create the structure or form of many pieces, as well as add interest...
to a narrow range of keys. The chords of the tonic C, dominant G and subdominant F are pure, as well as D, A, E and the minor chords Fm, Cm, Gm, Am, Bm and Em, but not the Dm.
A drawback of the asymmetric system is that it produces 14 wolf intervals, rather than 12 as for the symmetric ones (see below).
The B in the first symmetric scale differs from the B in the other scales by the syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
, being over 21 cents. In equally tempered scales, the difference is eliminated by making all steps the same frequency ratio.
The construction of the asymmetric scale is graphically shown in the picture. Each block has the height in cents of the constructive frequency ratios 2, 3 and 5. Recurring patterns can be recognised. For example, many times the next note is created by replacing a 5-block and a 3-block by four 2-blocks in the full picture and one in the simplified, or a ratio of 16/15.
For a similar image, where using frequency factors 2/1, 3/2, and 5/4, rather than 2, 3, and 5, see here.
The justest ratios
The just ratios used to build these scales can be used as a reference to evaluate the consonanceConsonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
of intervals in other scales (for instance, see this comparison table). However, 5-limit tuning is not the only method to obtain just intonation
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
. It is possible to construct just intervals with even "juster" ratios, or with values closer to the equal-tempered equivalents. For instance, a 7-limit tuning is sometimes used to obtain a slightly juster and consequently more consonant interval for the minor seventh (7/4) and its inversion, the major second (8/7). A list of these reference ratios, which may be referred to as pure or strictly just intervals or ratios, is provided below:
| Interval name | Short | Number of semitones |
5-limit tuning | 7-limit tuning | 17-limit tuning | |||
|---|---|---|---|---|---|---|---|---|
| Symmetric scales | Asymmetric scales | |||||||
| N. 1 | N. 2 | Standard | Extended | |||||
| Perfect unison | P1 | 0 | 1/1 | 1/1 | 1/1 | 1/1 | 1/1 | 1/1 |
| Minor second Minor second In modern Western tonal music theory a minor second is the interval between two notes on adjacent staff positions, or having adjacent note letters, whose alterations cause them to be one semitone or half-step apart, such as B and C or C and D.... |
m2 | 1 | 16/15 | 16/15 | 16/15 | 16/15 | 16/15 | 16/15 |
| Major second Major second In Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions... |
M2 | 2 | 9/8 | 10/9 | 9/8 | 9/8 | 8/7 | 8/7 |
| Minor third Minor third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major... |
m3 | 3 | 6/5 | 6/5 | 6/5 | 6/5 | 6/5 | 6/5 |
| Major third Major third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three... |
M3 | 4 | 5/4 | 5/4 | 5/4 | 5/4 | 5/4 | 5/4 |
| Perfect fourth Perfect fourth In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there... |
P4 | 5 | 4/3 | 4/3 | 4/3 | 4/3 | 4/3 | 4/3 |
| Augmented fourth | A4 | 6 | 45/32 | 45/32 | 45/32 | 25/18 | 7/5 Septimal tritone The lesser septimal tritone is the interval with ratio 7:5 . The inverse of that interval, the greater septimal tritone, is an interval with ratio 10:7... |
7/5 Septimal tritone The lesser septimal tritone is the interval with ratio 7:5 . The inverse of that interval, the greater septimal tritone, is an interval with ratio 10:7... or 17/12 |
| Diminished fifth | d5 | 6 | 64/45 | 64/45 | 64/45 | 36/25 | 10/7 | 10/7 or 24/17 |
| Perfect fifth Perfect fifth In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones... |
P5 | 7 | 3/2 | 3/2 | 3/2 | 3/2 | 3/2 | 3/2 |
| Minor sixth Minor sixth -Subminor sixth:In music, a subminor sixth or septimal sixth is an interval that is noticeably narrower than a minor sixth but noticeably wider than a diminished sixth.The sub-minor sixth is an interval of a 14:9 ratio or alternately 11:7.... |
m6 | 8 | 8/5 | 8/5 | 8/5 | 8/5 | 8/5 | 8/5 |
| Major sixth Major sixth In classical music from Western culture, a sixth is a musical interval encompassing six staff positions , and the major sixth is one of two commonly occurring sixths. It is qualified as major because it is the largest of the two... |
M6 | 9 | 5/3 | 5/3 | 5/3 | 5/3 | 5/3 | 5/3 |
| Minor seventh Minor seventh In classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the minor seventh is one of two commonly occurring sevenths. The minor quality specification identifies it as being the smallest of the two: the minor seventh spans ten semitones, the... |
m7 | 10 | 16/9 | 9/5 | 9/5 | 9/5 | 7/4 Harmonic seventh The harmonic seventh interval , also known as the septimal minor seventh, or subminor seventh, is one with an exact 7:4 ratio . This is somewhat narrower than and is "sweeter in quality" than an "ordinary" minor seventh, which has a just-intonation ratio of 9:5 , or an equal-temperament ratio of... |
7/4 Harmonic seventh The harmonic seventh interval , also known as the septimal minor seventh, or subminor seventh, is one with an exact 7:4 ratio . This is somewhat narrower than and is "sweeter in quality" than an "ordinary" minor seventh, which has a just-intonation ratio of 9:5 , or an equal-temperament ratio of... |
| Major seventh Major seventh In classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the major seventh is one of two commonly occurring sevenths. It is qualified as major because it is the larger of the two... |
M7 | 11 | 15/8 | 15/8 | 15/8 | 15/8 | 15/8 | |
| Perfect octave | P8 | 12 | 2/1 | 2/1 | 2/1 | 2/1 | 2/1 | |
Cells highlighted in yellow indicate intervals that are juster than those in the non-coloured cells in the same row. Those highlighted in cyan indicate even juster ratios. The symmetric scale 2 has not been shown because it is a solution equivalent to the symmetric scale 1 (with respect to which has one juster and one less just interval) and is not frequently used for comparisons.
Notice that the ratios 45/32 and 64/45 for the tritone
Tritone
In classical music from Western culture, the tritone |tone]]) is traditionally defined as a musical interval composed of three whole tones. In a chromatic scale, each whole tone can be further divided into two semitones...
s (augmented fourth and diminished fifth) are not in all contexts regarded as strictly just, but they are the justest possible in the above mentioned 5-limit tuning scales. An extended asymmetric 5-limit scale (see below) provides slightly juster ratios for both the tritones (25/18 and 36/25), the purity of which is also controversial. 7-limit tuning allows for the justest possible ratios, namely 7/5 (about 582.512 cents, also known as septimal tritone
Septimal tritone
The lesser septimal tritone is the interval with ratio 7:5 . The inverse of that interval, the greater septimal tritone, is an interval with ratio 10:7...
) and 10/7 (about 617.488 cents). These ratios are more consonant than 17/12 (about 603.000 cents) and 24/17 (about 597.000 cents), which can be obtained in 17-limit tuning, yet the latter are also fairly common, as they are closer to the equal-tempered value of 600.000 cents.
The above mentioned 7/4 interval (about 968.826 cents), also known as the septimal minor seventh, or harmonic seventh, has been a contentious issue throughout the history of music theory; it is 31 cents flatter than an equal-tempered minor seventh. Some assert the 7/4 is one of the blue note
Blue note
In jazz and blues, a blue note is a note sung or played at a slightly lower pitch than that of the major scale for expressive purposes. Typically the alteration is a semitone or less, but this varies among performers and genres. Country blues, in particular, features wide variations from the...
s used in jazz
Jazz
Jazz is a musical style that originated at the beginning of the 20th century in African American communities in the Southern United States. It was born out of a mix of African and European music traditions. From its early development until the present, jazz has incorporated music from 19th and 20th...
.
Size of intervals
The tables above show only the frequency ratios of each tone with respect to the base note C. However, intervals can be formed by starting from each of the twelve notes. Thus, twelve intervals can be defined for each interval type (twelve unisons, twelve semitoneSemitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s, twelve intervals composed of 2 semitones, twelve intervals composed of 3 semitones, etc.).
In 5-limit tuning, each of the interval types, except for the unisons and the octaves, has three or even four different sizes. This is the price paid for seeking just intonation. The tables on the right and below show their frequency ratios and their approximate sizes in cents, for the "asymmetric scale". Similar tables, for the "symmetric scale 1", are published here and here. Interval names are given in their standard shortened form. For instance, the size of the interval from C to G, which is a perfect fifth (P5), can be found in the seventh column of the row labeled C. Pure intervals, as defined above, are shown in bold font (notice that, as explained above, the justly intonated ratio 45/32 ≈ 590 cents, for A4, is not considered to be pure).
A color code is used to distinguish the intervals which deviate from the reference sizes shown in the construction table, and to show the amount of their deviation. Wolf intervals are marked in black.
The reason why the interval sizes vary throughout the scale is that the pitches forming the scale are unevenly spaced. Namely, the frequencies defined by construction for the twelve notes determine four different semitone
Semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s (i.e. intervals between adjacent notes). For instance:
-
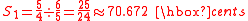
("Just" augmented unisonAugmented unisonIn modern Western tonal music theory an augmented unison is the interval between two notes on the same staff position, or having the same note letter, whose alterations cause them, in ordinary equal temperament, to be one semitone apart. In other words, it is a unison where one note has been raised...
between E and E) -

(Augmented unison between D and D) -

("Just" minor secondMinor secondIn modern Western tonal music theory a minor second is the interval between two notes on adjacent staff positions, or having adjacent note letters, whose alterations cause them to be one semitone or half-step apart, such as B and C or C and D....
between C and D) -
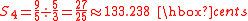
(Minor second between A and B)
Conversely, in an equally tempered chromatic scale, by definition the twelve pitches are equally spaced, all semitones having a size of exactly
As a consequence all intervals of any given type have the same size (e.g., all major thirds have the same size, all fifths have the same size, etc.). The price paid, in this case, is that none of them is justly tuned and perfectly consonant, except, of course, for the unison and the octave.
Note that 5-limit tuning was designed to maximize the number of pure intervals, but even in this system several intervals are markedly impure (for instance, as shown in the figures, 60 out of 144 intervals deviate by at least 19.6 cents from the justly intonated reference sizes shown in the construction table). Also, 5-limit tuning yields a much larger number of wolf intervals with respect to Pythagorean tuning, which can be considered a 3-limit just intonation tuning. Namely, while Pythagorean tuning determines only 2 wolf intervals (a fifth and a fourth), the 5-limit symmetric scales produce 12 of them, and the asymmetric scale 14. It is also important to note that the two fifths, three minor thirds, and three major sixths marked in orange in the tables (ratio 40/27, 32/27, and 27/16 (or G−, E−, and A+), even though they do not completely meet the conditions to be regarded as wolf intervals, deviate from the corresponding pure ratio by an amount (1 syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
, i.e. 81/80, or about 21.5 cents) large enough to be clearly perceived as dissonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
.
Clearly, the more we try to increase the number of pure and consonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
intervals, the more the remaining ones become impure and dissonant, by compensation. Some of the major seconds (M2) and minor sevenths (m7) represent the only exception to this rule. As you can see in the tables, those marked in orange are pure (10/9 and 16/9), even if their size is 81/80 narrower than the corresponding reference size (9/8 and 9/5).
For a comparison with other tuning systems, see also this table.
Commas
In other tuning systems, a commaComma (music)
In music theory, a comma is a minute interval, the difference resulting from tuning one note two different ways. The word "comma" used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F tuned using the D-based Pythagorean tuning...
may be defined as a minute interval, equal to the difference between two kinds of semitone
Semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s (diatonic and chromatic, also known as minor second, m2, or augmented unison, A1). In this case, however, 4 different kinds of semitones are produced (two A1, S1 and S2, and two m2, S3 and S4), and 12 different commas can be defined as the differences between their sizes in cents, or equivalently as the ratios between their ratios. Among these, we select the six ascending ones (those with ratio larger than 1/1, and positive size in cents):
| Name of comma Comma (music) In music theory, a comma is a minute interval, the difference resulting from tuning one note two different ways. The word "comma" used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F tuned using the D-based Pythagorean tuning... |
Equivalent definitions | Size | ||
|---|---|---|---|---|
| In meantone temperament Meantone temperament Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of... |
In 5-limit tuning (asymmetric scale) |
Ratio Interval ratio In music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth is 3:2 , 1.5, and may be approximated by an equal tempered perfect fifth which is 27/12, 1.498... |
Cents Cent (music) The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each... |
|
| Diaschisma Diaschisma The diaschisma is a small musical interval defined as the difference between three octaves and four perfect fifths plus two major thirds . It can be represented by the ratio 2048:2025 and is about 19.5 cents... (DS) |
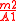 in 1/6-comma meantone Meantone temperament Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of... |
 |
 |
 |
| Syntonic comma Syntonic comma In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents... (SC) |
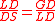 |
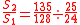 |
 |
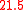 |
 |
||||
| Lesser diesis Diesis In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents... (LD) |
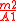 in 1/4-comma meantone Quarter-comma meantone Quarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning... |
 |
 |
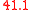 |
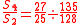 |
||||
| Greater diesis (GD) |  in 1/3-comma meantone |
 |
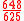 |
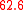 |
The other six ratios are discarded because they are just the opposite of these, and hence they have exactly the same length, but an opposite direction (i.e. a descending direction, a ratio smaller than 1/1, and a negative size in cents). We obtain commas of four different sizes: the diaschisma, the lesser diesis, the syntonic comma, and the greater diesis. Since S1 (the just A1) and S3 (the just m2) are the most often occurring semitones in this 12-tone scale (see tables above), the lesser diesis, being defined as the ratio between them, is the most often observed comma.
The syntonic comma is also defined, in 5-limit tuning, as the ratio between the major tone
Major second
In Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions...
(M2 with size 9/8) and the minor tone (M2 with size 10/9). Notice that it cannot be defined, in other tuning systems, as the ratio between diatonic and cromatic semitones (m2/A1), but it is an important reference value used to tune the perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
in any tuning system in the syntonic temperament
Syntonic temperament
The syntonic temperament is a system of musical tuning in which the frequency ratio of each musical interval is a product of powers of an octave and a tempered perfect fifth, with the width of the tempered major third being equal to four tempered perfect fifths minus two octaves and the width of...
continuum (including also meantone temperaments).
Diminished seconds
Three of the above mentioned commas, namely the diaschisma, the diesis and the greater diesis, meet the definition of the diminished secondDiminished second
In modern Western tonal music theory a diminished second is the interval between notes on two adjacent staff positions, or having adjacent note letters, whose alterations cause them, in ordinary equal temperament, to have no pitch difference, such as B and C or B and C...
, being the difference between the sizes in cents of a diatonic and a chromatic semitone (or equivalently the ratio between their frequency ratios).
On the contrary, the syntonic comma is defined either as the difference in cents between two chromatic semitones (S2 and S1), or between two diatonic semitones (S4 and S3), and cannot be considered to be a diminished second.
Extension of the twelve tone scale
The table above uses only low powers of 3 and 5 to build the base ratios. However, it can be easily extended by using higher positive and negative powers of the same numbers, such as 52 = 25, 5−2 = 1/25, 33 = 27, or 3−3 = 1/27. A scale with 25, 35, or even more pitches can be obtained by combining these base ratios.For instance, one can obtain 35 pitches by adding rows in each direction like this:
| Factor | 1/9 | 1/3 | 1 | 3 | 9 | |
|---|---|---|---|---|---|---|
| 125 | note ratio cents |
A 125/72 955.0 |
E 125/96 457.0 |
B 125/64 1158.9 |
F+ 375/256 660.9 |
C+ 1125/1024 162.9 |
| 25 | note ratio cents |
F 25/18 568.7 |
C 25/24 70.7 |
G 25/16 772.6 |
D 75/64 274.6 |
A+ 225/128 976.5 |
| 5 | note ratio cents |
D− 10/9 182.4 |
A 5/3 884.4 |
E 5/4 386.3 |
B 15/8 1088.3 |
F+ 45/32 590.2 |
| 1 | note ratio cents |
B− 16/9 996.1 |
F 4/3 498.0 |
C 1/1 0.0 |
G 3/2 702.0 |
D 9/8 203.9 |
| 1/5 | note ratio cents |
G− 64/45 609.8 |
D− 16/15 111.7 |
A 8/5 813.7 |
E 6/5 315.6 |
B 9/5 1017.6 |
| 1/25 | note ratio cents |
E− 256/225 223.5 |
B− 128/75 925.4 |
F 32/25 427.4 |
C 48/25 1129.3 |
G 36/25 631.3 |
| 1/125 | note ratio cents |
C− 2048/1125 1037.1 |
G− 512/375 539.1 |
D Diesis In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents... − 128/125 41.1 |
A 192/125 743.0 |
E 144/125 245.0 |
The left column (1/9) is sometimes removed (as in the asymmetric scale shown above), thus creating an asymmetric table with a smaller number of pitches. Notice that a juster ratio is produced for the diminished fifth (C-G = 36/25), with respect to the restricted 5-limit tuning described above (where C to G-
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
= 64/45).
History
In Pythagorean tuning, perhaps the first tuning system to be theorized in the West, the only highly consonant intervals were the perfect fifthPerfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
and its inversion, the perfect fourth
Perfect fourth
In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
. The Pythagorean major third
Major third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
(81:64) and minor third
Minor third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major...
(32:27) were dissonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
, and this prevented musicians from using triad
Triad (music)
In music and music theory, a triad is a three-note chord that can be stacked in thirds. Its members, when actually stacked in thirds, from lowest pitched tone to highest, are called:* the Root...
s and chord
Chord (music)
A chord in music is any harmonic set of two–three or more notes that is heard as if sounding simultaneously. These need not actually be played together: arpeggios and broken chords may for many practical and theoretical purposes be understood as chords...
s, forcing them for centuries to write music with relatively simple texture
Texture (music)
In music, texture is the way the melodic, rhythmic, and harmonic materials are combined in a composition , thus determining the overall quality of sound of a piece...
. In late Middle Ages
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
, musicians realized that by slightly tempering the pitch of some notes, the Pythagorean thirds could be made consonant
Consonance and dissonance
In music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
. For instance, if you decrease by a syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
(81:80) the frequency of E, C-E (a major third), and E-G (a minor third) become just. Namely, C-E is flattened to a justly intonated ratio of

and at the same time E-G is sharpened to the just ratio of
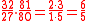
The drawback is that the fifths A-E and E-B, by flattening E, become almost as dissonant as the Pythagorean wolf fifth
Wolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
. But the fifth C-G stays consonant, since only E has been flattened (C-E * E-G = 5/4 * 6/5 = 3/2), and can be used together with C-E to produce a C-major
Major chord
In music theory, a major chord is a chord having a root, a major third, and a perfect fifth. When a chord has these three notes alone, it is called a major triad...
triad (C-E-G).
By generalizing this simple rationale, Gioseffo Zarlino
Gioseffo Zarlino
Gioseffo Zarlino was an Italian music theorist and composer of the Renaissance. He was possibly the most famous music theorist between Aristoxenus and Rameau, and made a large contribution to the theory of counterpoint as well as to musical tuning.-Life:Zarlino was born in Chioggia, near Venice...
, in the late sixteenth century, created the first justly intonated 7-tone (diatonic
Diatonic scale
In music theory, a diatonic scale is a seven note, octave-repeating musical scale comprising five whole steps and two half steps for each octave, in which the two half steps are separated from each other by either two or three whole steps...
) scale, which contained pure perfect fifths (3:2), pure major thirds, and pure minor thirds:
F → A → C → E → G → B → D
This is a sequence of just major thirds (M3, ratio 5:4) and just minor thirds (m3, ratio 6:5), starting from F:
F + M3 + m3 + M3 + m3 + M3 + m3
Since M3 + m3 = P5 (perfect fifth), i.e. 5/4 * 6/5 = 3/2, this is exactly equivalent to the diatonic scale obtained in 5-limit just intonation, and hence can be viewed as a subset of the construction table used for the 12-tone (chromatic
Chromatic scale
The chromatic scale is a musical scale with twelve pitches, each a semitone apart. On a modern piano or other equal-tempered instrument, all the half steps are the same size...
) scale:
| A | → | E | → | B | ||
| ↑ | ↑ | ↑ | ||||
| F | → | C | → | G | → | D |
where both rows are sequences of just fifths, and F-A, C-E, G-B are just major thirds:
| M3 | M3 | M3 | ||||
| + | + | + | ||||
| F | + | P5 | + | P5 | + | P5 |
See also
- Mathematics of musical scales
- Microtonal musicMicrotonal musicMicrotonal music is music using microtones—intervals of less than an equally spaced semitone. Microtonal music can also refer to music which uses intervals not found in the Western system of 12 equal intervals to the octave.-Terminology:...
- MicrotunerMicrotunerA microtuner or microtonal tuner is an electronic device or software program designed to modify and test the tuning of musical instruments with microtonal precision, allowing for the design and construction of microtonal scales and just intonation scales, and for tuning intervals that differ from...
- Pythagorean intervalPythagorean intervalIn musical tuning theory, a Pythagorean interval is a musical interval with frequency ratio equal to a power of two divided by a power of three, or vice versa...
- SemitoneSemitoneA semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
- List of intervals in 5-limit just intonation
- List of meantone intervals
- List of musical intervals
- Whole-tone scale
- Regular numberRegular numberRegular numbers are numbers that evenly divide powers of 60. As an example, 602 = 3600 = 48 × 75, so both 48 and 75 are divisors of a power of 60...
- HexanyHexanyIn music theory, the hexany is a six-note just intonation scale, with the notes placed on the vertices of an octahedron, equivalently the faces of a cube...
- Electronic tunerElectronic tunerThe term electronic tuner can refer to a number of different things, depending which discipline you wish to study.In the Discipline of radio frequency electronics an electronic tuner is a device which tunes across a part of the radio frequency spectrum by the application of a voltage or appropriate...
- Consonance and dissonanceConsonance and dissonanceIn music, a consonance is a harmony, chord, or interval considered stable, as opposed to a dissonance , which is considered to be unstable...
External links
- Art of the States: microtonal/just intonation works using just intonation by American composers
- The Chrysalis Foundation -- Just Intonation: Two Definitions
- Dante Rosati's 21 Tone Just Intonation guitar
- Just Intonation by Mark Nowitzky
- Just Intonation Explained by Kyle GannKyle GannKyle Eugene Gann is an American professor of music, critic and composer born in Dallas, Texas. As a critic for The Village Voice and other publications he has been a supporter of progressive music including such Downtown movements as postminimalism and totalism.- As composer :As a composer his...
- Just Intonation Network
- A selection of Just Intonation works edited by the Just Intonation Network web published on the Tellus Audio Cassette MagazineTellus Audio Cassette MagazineLaunched from the Lower East Side, Manhattan, in 1983 as a subscription only bimonthly publication, the Tellus cassette series took full advantage of the popular cassette medium to promote cutting-edge downtown music, documenting the New York scene and advancing experimental composers of the time...
project archive at UbuwebUbuWebUbuWeb is a large web-based educational resource for avant-garde material available on the internet, founded in 1996 by poet Kenneth Goldsmith. It offers visual, concrete and sound poetry, expanding to include film and sound art mp3 archives.-Philosophy:... - Medieval Music and Arts Foundation
- Music Novatory - Just Intonation
- Why does Just Intonation sound so good?
- The Wilson Archives
- Barbieri, Patrizio. Enharmonic instruments and music, 1470-1900. (2008) Latina, Il Levante
- 22 Note Just Intonation Keyboard Software with 12 Indian Instrument Sounds Libreria Editrice
- PLAINSOUND MUSIC EDITION - JI music and research, information about the Helmholtz-Ellis JI Pitch Notation