
Entropy of mixing
Encyclopedia
In thermodynamics
the entropy of mixing is the increase in the total entropy
of a compound system, when different and chemically non-reacting chemical substance
s or material components
are mixed by removing partition(s) between the system's initially separate volumes. The materials are each at a common temperature and pressure, and the whole compound system may change its volume, while being maintained at constant temperature, pressure, and chemical component masses. The volume available for each material to explore is increased, from that of its initially separate compartment, to the total common final volume. The final volume need not be the sum of the initially separate volumes, so that work can be done on or by the system during the process of mixing, as well as heat being transferred to or from the surroundings, because of the maintenance of constant pressure and temperature.
For concision in this article, the term 'ideal material' is used to refer to an ideal gas
(mixture) or an ideal solution
.
In a process of mixing of ideal materials, the final common volume is the sum of the initial separate compartment volumes. There is no heat transfer and no work is done. The entropy of mixing is entirely accounted for by the diffusive expansion of each material into a final volume not initially accessible to it.
On the mixing of non-ideal materials, the total final common volume may be different from the sum of the separate initial volumes, and there may occur transfer of work or heat, to or from the surroundings; also there may be a departure of the entropy of mixing from that of the corresponding ideal case. That departure is the main reason for interest in entropy of mixing. These energy and entropy variables and their temperature dependences provide valuable information about the properties of the materials.
On a molecular level, the entropy of mixing is of interest because it is a macroscopic variable that provides information about molecular properties. In ideal materials, intermolecular forces are the same between every pair of molecular kinds, so that a molecule feels no difference between itself and its molecular neighbours. Consequently, there may be differences of intermolecular forces or specific molecular effects between different species, even though they are chemically non-reacting. The entropy of mixing provides information about differences of intermolecular forces or specific molecular effects in the materials.
The statistical concept of randomness is used for statistical mechanical explanation of the entropy of mixing. Mixing of ideal materials is regarded as random at a molecular level, and, correspondingly, mixing of non-ideal materials may be non-random.
For example, two ideal gases, at the same temperature and pressure, are initially separated by a dividing partition.
Upon removal of the dividing partition, they expand into a final common volume (the sum of the two initial volumes), and the entropy of mixing
 is given by
is given by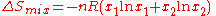 .
.
where is the gas constant
is the gas constant
, the total number of moles
the total number of moles
and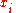 the mole fraction of component
the mole fraction of component 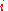 which initially occupies volume
which initially occupies volume 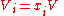 . After the removal of the partition, the
. After the removal of the partition, the  moles of component
moles of component 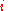 may explore the combined volume
may explore the combined volume 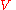 , which causes an entropy increase equal to
, which causes an entropy increase equal to  for each component gas.
for each component gas.
In this case, the increase in entropy is due entirely to the irreversible processes of expansion of the two gases, and involves no heat or work flow between the system and its surroundings.
change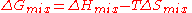 determines whether mixing at constant (absolute) temperature
determines whether mixing at constant (absolute) temperature 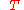 and pressure
and pressure  is a spontaneous process
is a spontaneous process
. This quantity combines two physical effects - the enthalpy
of mixing which is a measure of the energy change, and the entropy of mixing considered here.
For an ideal gas
mixture or an ideal solution
, there is no enthalpy of mixing (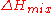 ), so that the Gibbs free energy of mixing is given by the entropy term only:
), so that the Gibbs free energy of mixing is given by the entropy term only: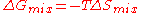
For an ideal solution, the Gibbs free energy of mixing is always negative, meaning that mixing as ideal solutions is always spontaneous. The lowest value is when the mole fraction is 0.5 for a mixture of two components, or 1/n for a mixture of n components.
s and for regular solution
s, and approximately so for many real solutions.
For binary mixtures the entropy of random mixing can be considered as a function of the mole fraction of one component.
For all possible mixtures, , so that
, so that 
 and
and 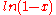 are both negative and the entropy of mixing
are both negative and the entropy of mixing  is positive and favors mixing of the pure components.
is positive and favors mixing of the pure components.
Also the curvature of as a function of
as a function of  is given by the second derivative
is given by the second derivative 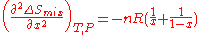
This curvature is negative for all possible mixtures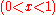 , so that mixing two solutions to form a solution of intermediate composition will also increase the entropy of the system. Random mixing therefore always favors miscibility and opposes phase separation.
, so that mixing two solutions to form a solution of intermediate composition will also increase the entropy of the system. Random mixing therefore always favors miscibility and opposes phase separation.
For ideal solutions, the enthalpy of mixing is zero so that the components are miscible in all proportions. For regular solutions a positive enthalpy of mixing may cause incomplete miscibility (phase separation for some compositions) at temperatures below the upper critical solution temperature
(UCST). This is the minimum temperature at which the term in the Gibbs energy of mixing is sufficient to produce miscibility in all proportions.
term in the Gibbs energy of mixing is sufficient to produce miscibility in all proportions.
(LCST) or lower limiting temperature for phase separation.
For example, triethylamine
and water are miscible in all proportions below 19oC, but above this critical temperature, solutions of certain compositions separate into two phases at equilibrium with each other. This means that is negative for mixing of the two phases below 19oC and positive above this temperature. Therefore
is negative for mixing of the two phases below 19oC and positive above this temperature. Therefore 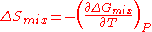 is negative for mixing of these two equilibrium phases. This is due to the formation of attractive hydrogen bond
is negative for mixing of these two equilibrium phases. This is due to the formation of attractive hydrogen bond
s between the two components which prevent random mixing. Triethylamine molecules cannot form hydrogen bonds with each other but only with water molecules, so in solution they remain associated to water molecules with loss of entropy. The mixing which occurs below 19oC is due not to entropy but to the enthalpy of formation of the hydrogen bonds.
Lower critical solution temperatures also occur in many polymer-solvent mixtures. For polar systems such as polyacrylic acid
in 1,4-dioxane
, this is often due to the formation of hydrogen bonds between polymer and solvent. For nonpolar systems such as polystyrene
in cyclohexane
, phase separation has been observed in sealed tubes (at high pressure) at temperatures approaching the liquid-vapor critical point
of the solvent. At such temperatures the solvent expands much more rapidly than the polymer, whose segments are covalently linked. Mixing therefore requires contraction of the solvent for compatibility of the polymer, resulting in a loss of entropy.
.) This is a crystal
-like conceptual model
to identify the molecular centers of mass
. If the two phases
are liquid
s, there is no spatial uncertainty in each one individually. (This is, of course, an approximation. Liquids have a “free volume” which is why they are (usually) less dense
than solid
s.) Everywhere we look in component 1, there is a molecule present, and likewise for component 2. After the two different substances are intermingled (assuming they are miscible), the liquid is still dense with molecules, but now there is uncertainty about what kind of molecule is in which location. Of course, any idea of identifying molecules in given locations is a thought experiment
, not something one could do, but the calculation of the uncertainty is well-defined.
We can use Boltzmann's equation
for the entropy change as applied to the mixing process

where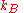 is Boltzmann’s constant. We then calculate the number of ways
is Boltzmann’s constant. We then calculate the number of ways  of arranging
of arranging 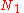 molecules of component 1 and
molecules of component 1 and 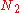 molecules of component 2 on a lattice, where
molecules of component 2 on a lattice, where
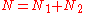
is the total number of molecules, and therefore the number of lattice sites.
Calculating the number of permutations of objects, correcting for the fact that
objects, correcting for the fact that  of them are identical to one another, and likewise for
of them are identical to one another, and likewise for 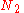 ,
,
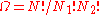
After applying Stirling's approximation
for the factorial
of a large integer m: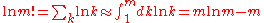 ,
,
the result is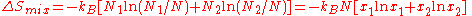
where we have introduced the mole fractions, which are also the probabilities
of finding any particular component in a given lattice site.
Since the Boltzmann constant , where
, where  is Avogadro's number, and the number of molecules
is Avogadro's number, and the number of molecules 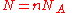 , we recover the thermodynamic expression for the mixing of two ideal gases,
, we recover the thermodynamic expression for the mixing of two ideal gases, 
This expression can be generalized to a mixture of components,
components, 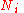 , with
, with 
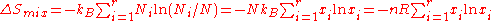
, which is defined without requiring Stirling's approximation. Claude Shannon
introduced this expression for use in information theory
, but similar formulas can be found as far back as the work of Ludwig Boltzmann
and J. Willard Gibbs
. The Shannon uncertainty is completely unrelated to the Heisenberg
uncertainty principle
in quantum mechanics
, and is defined by

To relate this quantity to the entropy of mixing, we consider that the summation is over the various chemical species, so that this is the uncertainty about which kind of molecule is in any one site. It must be multiplied by the number of sites to get the uncertainty for the whole system. Since the probability
to get the uncertainty for the whole system. Since the probability 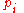 of finding species
of finding species 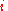 in a given site equals the mole fraction
in a given site equals the mole fraction  , we again obtain the entropy of mixing on multiplying by the Boltzmann constant
, we again obtain the entropy of mixing on multiplying by the Boltzmann constant 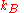 .
.
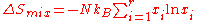
also join. The total number of empty cells is the sum of the numbers of empty cells in the two components prior to mixing. Consequently, that part of the spatial uncertainty concerning whether any molecule is present in a lattice cell is the sum of the initial values, and does not increase upon "mixing".
Almost everywhere we look, we find empty lattice cells. But we do find molecules in those few cells which are occupied. When there is real mixing, for each cell occupied, there is a contingent uncertainty about which kind of molecule it is. When there is no real mixing because the two substances are identical, there is no uncertainty about which kind of molecule it is. Using conditional probabilities, it turns out that the analytical problem for the small subset
of occupied cells is exactly the same as for mixed liquids, and the increase in the entropy, or spatial uncertainty, has exactly the same form as obtained previously. Obviously the subset of occupied cells is not the same at different times. But only when there is real mixing and an occupied cell is found do we ask which kind of molecule is there.
See also: Gibbs paradox
, in which it would seem that "mixing" two samples of the same gas would produce entropy.
is a crystal
line solid
, the argument is much the same. A crystal has no spatial uncertainty at all, except for crystallographic defect
s, and a (perfect) crystal allows us to localize the molecules using the crystal symmetry group
. The fact that volumes do not add when dissolving a solid in a liquid is not important for condensed phase
s. If the solute is not crystalline, we can still use a spatial lattice, as good an approximation for an amorphous solid as it is for a liquid.
The Flory-Huggins solution theory
provides the entropy of mixing for polymer
solutions, in which the macromolecule
s are huge compared to the solvent molecules. In this case, the assumption is made that each monomer
subunit in the polymer chain occupies a lattice site.
Note that solids in contact with each other also slowly interdiffuse
, and solid mixtures of two or more components may be made at will (alloy
s, semiconductor
s, etc.). Again, the same equations for the entropy of mixing apply, but only for homogeneous, uniform phases.
According to Fowler and Guggenheim (1939/1965), the conflating of the just-mentioned two mechanisms for the entropy of mixing is well established in customary terminology, but can be confusing unless it is borne in mind that the independent variables are the common initial and final temperature and total pressure; if the respective partial pressures or the total volume are chosen as independent variables instead of the total pressure, the description is different.
In contrast to the established customary usage, "mixing" might be conducted at constant volume for each of two fixed masses of gases of equal volume, being mixed by gradually merging their initially separate volumes by use of two ideal semipermeable membranes, each permeable only to one of the respective gases, so that the respective volumes available to each gas remain constant during the merge; either one of the common temperature or the common pressure is chosen to be independently controlled by the experimenter, the other being allowed to vary so as to maintain constant volume for each mass of gas. In this kind of "mixing", the final common volume is equal to each of the respective separate initial volumes, and each gas finally occupies the same volume as it did initially.
This kind of "mixing", in the special case of perfect gases, is referred to in what is sometimes called Gibbs' theorem. It states that the entropy of such "mixing" is zero.
" which states that if the molecular species are identical, there will be no entropy change, because, as defined in proper thermodynamic terms, there is no process and no mixing, yet the slightest detectable distinction between the two will yield a thermodynamically recognized process of mixing and a considerable entropy change, which is just the entropy of mixing. The word "paradox" is used here to refer to the specious appearance that a slightest detectable distinction can lead to a considerably large change. For ideal gases, the entropy of mixing does not depend on the degree of difference between the distinct molecular species, but only on the fact that they are distinct; for non-ideal gases, the entropy of mixing can depend on the degree of difference of the distinct molecular species. The specious "mixing" of identical molecular species is not in thermodynamic terms a mixing at all, because thermodynamics refers to states specified by state variables, not allowing talk of an imaginary labelling of particles. If the molecular species are different, then there is mixing in the thermodynamic sense; but if they are the same then there is no mixing in the thermodynamic sense.
Gibbs himself was clearly aware of the physics here, and he did not say that he saw any paradox in it. The "paradox" is the work of textbook writers.
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
the entropy of mixing is the increase in the total entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of a compound system, when different and chemically non-reacting chemical substance
Chemical substance
In chemistry, a chemical substance is a form of matter that has constant chemical composition and characteristic properties. It cannot be separated into components by physical separation methods, i.e. without breaking chemical bonds. They can be solids, liquids or gases.Chemical substances are...
s or material components
Component (thermodynamics)
In thermodynamics, a component is a chemically distinct constituent ofa system. Calculating the number of components in a system is necessary, for example, when applying Gibbs phase rule in determination of the number of degrees of freedom of a system....
are mixed by removing partition(s) between the system's initially separate volumes. The materials are each at a common temperature and pressure, and the whole compound system may change its volume, while being maintained at constant temperature, pressure, and chemical component masses. The volume available for each material to explore is increased, from that of its initially separate compartment, to the total common final volume. The final volume need not be the sum of the initially separate volumes, so that work can be done on or by the system during the process of mixing, as well as heat being transferred to or from the surroundings, because of the maintenance of constant pressure and temperature.
For concision in this article, the term 'ideal material' is used to refer to an ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
(mixture) or an ideal solution
Ideal solution
In chemistry, an ideal solution or ideal mixture is a solution with thermodynamic properties analogous to those of a mixture of ideal gases. The enthalpy of solution is zero as is the volume change on mixing; the closer to zero the enthalpy of solution is, the more "ideal" the behavior of the...
.
In a process of mixing of ideal materials, the final common volume is the sum of the initial separate compartment volumes. There is no heat transfer and no work is done. The entropy of mixing is entirely accounted for by the diffusive expansion of each material into a final volume not initially accessible to it.
On the mixing of non-ideal materials, the total final common volume may be different from the sum of the separate initial volumes, and there may occur transfer of work or heat, to or from the surroundings; also there may be a departure of the entropy of mixing from that of the corresponding ideal case. That departure is the main reason for interest in entropy of mixing. These energy and entropy variables and their temperature dependences provide valuable information about the properties of the materials.
On a molecular level, the entropy of mixing is of interest because it is a macroscopic variable that provides information about molecular properties. In ideal materials, intermolecular forces are the same between every pair of molecular kinds, so that a molecule feels no difference between itself and its molecular neighbours. Consequently, there may be differences of intermolecular forces or specific molecular effects between different species, even though they are chemically non-reacting. The entropy of mixing provides information about differences of intermolecular forces or specific molecular effects in the materials.
The statistical concept of randomness is used for statistical mechanical explanation of the entropy of mixing. Mixing of ideal materials is regarded as random at a molecular level, and, correspondingly, mixing of non-ideal materials may be non-random.
Mixing of ideal materials at constant temperature and pressure
In ideal materials, intermolecular forces are the same between every pair of molecular kinds, so that a molecule feels no difference between itself and its molecular neighbours. This is the reference case against which are examined corresponding mixings of non-ideal materials.For example, two ideal gases, at the same temperature and pressure, are initially separated by a dividing partition.
Upon removal of the dividing partition, they expand into a final common volume (the sum of the two initial volumes), and the entropy of mixing
 is given by
is given by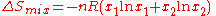 .
.where
 is the gas constant
is the gas constantGas constant
The gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
,
 the total number of moles
the total number of molesMole (unit)
The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
and
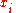 the mole fraction of component
the mole fraction of component 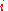 which initially occupies volume
which initially occupies volume 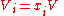 . After the removal of the partition, the
. After the removal of the partition, the  moles of component
moles of component 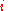 may explore the combined volume
may explore the combined volume 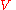 , which causes an entropy increase equal to
, which causes an entropy increase equal to  for each component gas.
for each component gas.In this case, the increase in entropy is due entirely to the irreversible processes of expansion of the two gases, and involves no heat or work flow between the system and its surroundings.
Gibbs free energy of mixing
The Gibbs free energyGibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
change
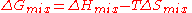 determines whether mixing at constant (absolute) temperature
determines whether mixing at constant (absolute) temperature 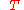 and pressure
and pressure  is a spontaneous process
is a spontaneous processSpontaneous process
A spontaneous process is the time-evolution of a system in which it releases free energy and moves to a lower, more thermodynamically stable energy state...
. This quantity combines two physical effects - the enthalpy
Enthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
of mixing which is a measure of the energy change, and the entropy of mixing considered here.
For an ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
mixture or an ideal solution
Ideal solution
In chemistry, an ideal solution or ideal mixture is a solution with thermodynamic properties analogous to those of a mixture of ideal gases. The enthalpy of solution is zero as is the volume change on mixing; the closer to zero the enthalpy of solution is, the more "ideal" the behavior of the...
, there is no enthalpy of mixing (
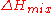 ), so that the Gibbs free energy of mixing is given by the entropy term only:
), so that the Gibbs free energy of mixing is given by the entropy term only: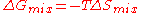
For an ideal solution, the Gibbs free energy of mixing is always negative, meaning that mixing as ideal solutions is always spontaneous. The lowest value is when the mole fraction is 0.5 for a mixture of two components, or 1/n for a mixture of n components.
Ideal and regular solutions
The above equation for the entropy of mixing of ideal gases is valid also for certain liquid (or solid) solutions - those which are formed by completely random mixing so that the components move independently in the total volume. Such random mixing of solutions occurs if the interaction energies between unlike molecules are similar to the average interaction energies between like molecules. The value of the entropy corresponds exactly to random mixing for ideal solutionIdeal solution
In chemistry, an ideal solution or ideal mixture is a solution with thermodynamic properties analogous to those of a mixture of ideal gases. The enthalpy of solution is zero as is the volume change on mixing; the closer to zero the enthalpy of solution is, the more "ideal" the behavior of the...
s and for regular solution
Regular solution
In chemistry, a regular solution is a solution that diverges from the behavior of an ideal solution only moderately. Its entropy of mixing is equal to that of an ideal solution with the same composition, due to random mixing without strong specific interactions...
s, and approximately so for many real solutions.
For binary mixtures the entropy of random mixing can be considered as a function of the mole fraction of one component.

For all possible mixtures,
 , so that
, so that 
 and
and 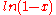 are both negative and the entropy of mixing
are both negative and the entropy of mixing  is positive and favors mixing of the pure components.
is positive and favors mixing of the pure components.Also the curvature of
 as a function of
as a function of  is given by the second derivative
is given by the second derivative 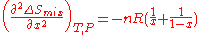
This curvature is negative for all possible mixtures
 , so that mixing two solutions to form a solution of intermediate composition will also increase the entropy of the system. Random mixing therefore always favors miscibility and opposes phase separation.
, so that mixing two solutions to form a solution of intermediate composition will also increase the entropy of the system. Random mixing therefore always favors miscibility and opposes phase separation.For ideal solutions, the enthalpy of mixing is zero so that the components are miscible in all proportions. For regular solutions a positive enthalpy of mixing may cause incomplete miscibility (phase separation for some compositions) at temperatures below the upper critical solution temperature
Upper critical solution temperature
The upper critical solution temperature or upper consolute temperature is the critical temperature above which the components of a mixture are miscible in all proportions. The word upper indicates that the UCST is an upper bound to a temperature range of partial miscibility, or miscibility for...
(UCST). This is the minimum temperature at which the
 term in the Gibbs energy of mixing is sufficient to produce miscibility in all proportions.
term in the Gibbs energy of mixing is sufficient to produce miscibility in all proportions.Systems with a lower critical solution temperature
Nonrandom mixing with a lower entropy of mixing can occur when the attractive interactions between unlike molecules are significantly stronger (or weaker) than the mean interactions between like molecules. For some systems this can lead to a lower critical solution temperatureLower critical solution temperature
The lower critical solution temperature or lower consolute temperature is the critical temperature below which the components of a mixture are miscible for all compositions...
(LCST) or lower limiting temperature for phase separation.
For example, triethylamine
Triethylamine
Triethylamine is the chemical compound with the formula N3, commonly abbreviated Et3N. It is also abbreviated TEA, yet this abbreviation must be used carefully to avoid confusion with triethanolamine, for which TEA is also a common abbreviation....
and water are miscible in all proportions below 19oC, but above this critical temperature, solutions of certain compositions separate into two phases at equilibrium with each other. This means that
 is negative for mixing of the two phases below 19oC and positive above this temperature. Therefore
is negative for mixing of the two phases below 19oC and positive above this temperature. Therefore 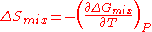 is negative for mixing of these two equilibrium phases. This is due to the formation of attractive hydrogen bond
is negative for mixing of these two equilibrium phases. This is due to the formation of attractive hydrogen bondHydrogen bond
A hydrogen bond is the attractive interaction of a hydrogen atom with an electronegative atom, such as nitrogen, oxygen or fluorine, that comes from another molecule or chemical group. The hydrogen must be covalently bonded to another electronegative atom to create the bond...
s between the two components which prevent random mixing. Triethylamine molecules cannot form hydrogen bonds with each other but only with water molecules, so in solution they remain associated to water molecules with loss of entropy. The mixing which occurs below 19oC is due not to entropy but to the enthalpy of formation of the hydrogen bonds.
Lower critical solution temperatures also occur in many polymer-solvent mixtures. For polar systems such as polyacrylic acid
Polyacrylic acid
Poly or PAA or Carbomer is a type of anionic polymer. The monomer of poly is acrylic acid. In a water solution at neutral pH, many of the side chains of PAA will lose their protons and acquire a negative charge. This makes PAA a polyelectrolyte.Dry PAA is a white solid...
in 1,4-dioxane
1,4-Dioxane
1,4-Dioxane, often called dioxane because the other isomers of dioxane are rare, is a heterocyclic organic compound. It is a colorless liquid with a faint sweet odor similar to that of diethyl ether. It is classified as an ether. This colorless liquid is mainly used as a stabilizer for the solvent...
, this is often due to the formation of hydrogen bonds between polymer and solvent. For nonpolar systems such as polystyrene
Polystyrene
Polystyrene ) also known as Thermocole, abbreviated following ISO Standard PS, is an aromatic polymer made from the monomer styrene, a liquid hydrocarbon that is manufactured from petroleum by the chemical industry...
in cyclohexane
Cyclohexane
Cyclohexane is a cycloalkane with the molecular formula C6H12. Cyclohexane is used as a nonpolar solvent for the chemical industry, and also as a raw material for the industrial production of adipic acid and caprolactam, both of which being intermediates used in the production of nylon...
, phase separation has been observed in sealed tubes (at high pressure) at temperatures approaching the liquid-vapor critical point
Critical point (thermodynamics)
In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
of the solvent. At such temperatures the solvent expands much more rapidly than the polymer, whose segments are covalently linked. Mixing therefore requires contraction of the solvent for compatibility of the polymer, resulting in a loss of entropy.
Statistical thermodynamical explanation of the entropy of mixing of ideal gases
Since thermodynamic entropy can be related to statistical mechanics or to information theory, it is possible to calculate the entropy of mixing using these two approaches. Here we consider the simple case of mixing ideal gases.Proof from statistical mechanics
Assume that the molecules of two different substances are approximately the same size, and regard space as subdivided into a square lattice whose cells are the size of the molecules. (In fact, any lattice would do, including close packingClose-packing
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement . Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a regular lattice...
.) This is a crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
-like conceptual model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
to identify the molecular centers of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
. If the two phases
Phase (matter)
In the physical sciences, a phase is a region of space , throughout which all physical properties of a material are essentially uniform. Examples of physical properties include density, index of refraction, and chemical composition...
are liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
s, there is no spatial uncertainty in each one individually. (This is, of course, an approximation. Liquids have a “free volume” which is why they are (usually) less dense
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
than solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
s.) Everywhere we look in component 1, there is a molecule present, and likewise for component 2. After the two different substances are intermingled (assuming they are miscible), the liquid is still dense with molecules, but now there is uncertainty about what kind of molecule is in which location. Of course, any idea of identifying molecules in given locations is a thought experiment
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
, not something one could do, but the calculation of the uncertainty is well-defined.
We can use Boltzmann's equation
Boltzmann's entropy formula
In statistical thermodynamics, Boltzmann's equation is a probability equation relating the entropy S of an ideal gas to the quantity W, which is the number of microstates corresponding to a given macrostate:...
for the entropy change as applied to the mixing process

where
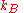 is Boltzmann’s constant. We then calculate the number of ways
is Boltzmann’s constant. We then calculate the number of ways  of arranging
of arranging 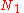 molecules of component 1 and
molecules of component 1 and 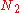 molecules of component 2 on a lattice, where
molecules of component 2 on a lattice, where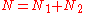
is the total number of molecules, and therefore the number of lattice sites.
Calculating the number of permutations of
 objects, correcting for the fact that
objects, correcting for the fact that  of them are identical to one another, and likewise for
of them are identical to one another, and likewise for 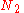 ,
,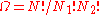
After applying Stirling's approximation
Stirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
for the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
of a large integer m:
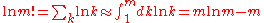 ,
,the result is
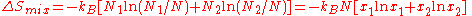
where we have introduced the mole fractions, which are also the probabilities
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of finding any particular component in a given lattice site.
Since the Boltzmann constant
 , where
, where  is Avogadro's number, and the number of molecules
is Avogadro's number, and the number of molecules 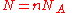 , we recover the thermodynamic expression for the mixing of two ideal gases,
, we recover the thermodynamic expression for the mixing of two ideal gases, 
This expression can be generalized to a mixture of
 components,
components, 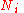 , with
, with 
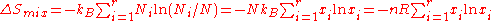
Relationship to information theory
The entropy of mixing is also proportional to the Shannon entropy or compositional uncertainty of information theoryInformation theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, which is defined without requiring Stirling's approximation. Claude Shannon
Claude Elwood Shannon
Claude Elwood Shannon was an American mathematician, electronic engineer, and cryptographer known as "the father of information theory"....
introduced this expression for use in information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, but similar formulas can be found as far back as the work of Ludwig Boltzmann
Ludwig Boltzmann
Ludwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...
and J. Willard Gibbs
Josiah Willard Gibbs
Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...
. The Shannon uncertainty is completely unrelated to the Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, and is defined by

To relate this quantity to the entropy of mixing, we consider that the summation is over the various chemical species, so that this is the uncertainty about which kind of molecule is in any one site. It must be multiplied by the number of sites
 to get the uncertainty for the whole system. Since the probability
to get the uncertainty for the whole system. Since the probability 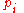 of finding species
of finding species 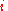 in a given site equals the mole fraction
in a given site equals the mole fraction  , we again obtain the entropy of mixing on multiplying by the Boltzmann constant
, we again obtain the entropy of mixing on multiplying by the Boltzmann constant 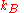 .
.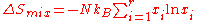
Application to gases
In gases there is a lot more spatial uncertainty because most of their volume is merely empty space. We can regard the mixing process as allowing the contents of the two originally separate contents to expand into the combined volume of the two conjoined containers. The two lattices which allow us to conceptually localize molecular centers of massCenter of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
also join. The total number of empty cells is the sum of the numbers of empty cells in the two components prior to mixing. Consequently, that part of the spatial uncertainty concerning whether any molecule is present in a lattice cell is the sum of the initial values, and does not increase upon "mixing".
Almost everywhere we look, we find empty lattice cells. But we do find molecules in those few cells which are occupied. When there is real mixing, for each cell occupied, there is a contingent uncertainty about which kind of molecule it is. When there is no real mixing because the two substances are identical, there is no uncertainty about which kind of molecule it is. Using conditional probabilities, it turns out that the analytical problem for the small subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of occupied cells is exactly the same as for mixed liquids, and the increase in the entropy, or spatial uncertainty, has exactly the same form as obtained previously. Obviously the subset of occupied cells is not the same at different times. But only when there is real mixing and an occupied cell is found do we ask which kind of molecule is there.
See also: Gibbs paradox
Gibbs paradox
In statistical mechanics, a semi-classical derivation of the entropy that doesn't take into account the indistinguishability of particles, yields an expression for the entropy which is not extensive...
, in which it would seem that "mixing" two samples of the same gas would produce entropy.
Application to solutions
If the soluteSolution
In chemistry, a solution is a homogeneous mixture composed of only one phase. In such a mixture, a solute is dissolved in another substance, known as a solvent. The solvent does the dissolving.- Types of solutions :...
is a crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
line solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
, the argument is much the same. A crystal has no spatial uncertainty at all, except for crystallographic defect
Crystallographic defect
Crystalline solids exhibit a periodic crystal structure. The positions of atoms or molecules occur on repeating fixed distances, determined by the unit cell parameters. However, the arrangement of atom or molecules in most crystalline materials is not perfect...
s, and a (perfect) crystal allows us to localize the molecules using the crystal symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
. The fact that volumes do not add when dissolving a solid in a liquid is not important for condensed phase
Phase (matter)
In the physical sciences, a phase is a region of space , throughout which all physical properties of a material are essentially uniform. Examples of physical properties include density, index of refraction, and chemical composition...
s. If the solute is not crystalline, we can still use a spatial lattice, as good an approximation for an amorphous solid as it is for a liquid.
The Flory-Huggins solution theory
Flory-Huggins solution theory
Flory-Huggins solution theory is a mathematical model of the thermodynamics of polymer solutions which takes account of the great dissimilarity in molecular sizes in adapting the usual expression for the entropy of mixing. The result is an equation for the Gibbs free energy change \Delta G_m for...
provides the entropy of mixing for polymer
Polymer
A polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...
solutions, in which the macromolecule
Macromolecule
A macromolecule is a very large molecule commonly created by some form of polymerization. In biochemistry, the term is applied to the four conventional biopolymers , as well as non-polymeric molecules with large molecular mass such as macrocycles...
s are huge compared to the solvent molecules. In this case, the assumption is made that each monomer
Monomer
A monomer is an atom or a small molecule that may bind chemically to other monomers to form a polymer; the term "monomeric protein" may also be used to describe one of the proteins making up a multiprotein complex...
subunit in the polymer chain occupies a lattice site.
Note that solids in contact with each other also slowly interdiffuse
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
, and solid mixtures of two or more components may be made at will (alloy
Alloy
An alloy is a mixture or metallic solid solution composed of two or more elements. Complete solid solution alloys give single solid phase microstructure, while partial solutions give two or more phases that may or may not be homogeneous in distribution, depending on thermal history...
s, semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
s, etc.). Again, the same equations for the entropy of mixing apply, but only for homogeneous, uniform phases.
Mixing with and without change of available volume
In the established customary usage, expressed in the lead section of this article, the entropy of mixing comes from two mechanisms, the intermingling and possible interactions of the distinct molecular species, and the change in the volume available for each molecular species, or the change in concentration of each molecular species. For ideal gases, the entropy of mixing has nothing to do with mixing in the sense of intermingling and interactions of molecular species, but is only to do with expansion into the common volume.According to Fowler and Guggenheim (1939/1965), the conflating of the just-mentioned two mechanisms for the entropy of mixing is well established in customary terminology, but can be confusing unless it is borne in mind that the independent variables are the common initial and final temperature and total pressure; if the respective partial pressures or the total volume are chosen as independent variables instead of the total pressure, the description is different.
In contrast to the established customary usage, "mixing" might be conducted at constant volume for each of two fixed masses of gases of equal volume, being mixed by gradually merging their initially separate volumes by use of two ideal semipermeable membranes, each permeable only to one of the respective gases, so that the respective volumes available to each gas remain constant during the merge; either one of the common temperature or the common pressure is chosen to be independently controlled by the experimenter, the other being allowed to vary so as to maintain constant volume for each mass of gas. In this kind of "mixing", the final common volume is equal to each of the respective separate initial volumes, and each gas finally occupies the same volume as it did initially.
This kind of "mixing", in the special case of perfect gases, is referred to in what is sometimes called Gibbs' theorem. It states that the entropy of such "mixing" is zero.
Gibbs' paradox: "mixing" of identical species
The molecular species must be distinct for the entropy of mixing to exist. Thus arises the so-called "Gibbs paradoxGibbs paradox
In statistical mechanics, a semi-classical derivation of the entropy that doesn't take into account the indistinguishability of particles, yields an expression for the entropy which is not extensive...
" which states that if the molecular species are identical, there will be no entropy change, because, as defined in proper thermodynamic terms, there is no process and no mixing, yet the slightest detectable distinction between the two will yield a thermodynamically recognized process of mixing and a considerable entropy change, which is just the entropy of mixing. The word "paradox" is used here to refer to the specious appearance that a slightest detectable distinction can lead to a considerably large change. For ideal gases, the entropy of mixing does not depend on the degree of difference between the distinct molecular species, but only on the fact that they are distinct; for non-ideal gases, the entropy of mixing can depend on the degree of difference of the distinct molecular species. The specious "mixing" of identical molecular species is not in thermodynamic terms a mixing at all, because thermodynamics refers to states specified by state variables, not allowing talk of an imaginary labelling of particles. If the molecular species are different, then there is mixing in the thermodynamic sense; but if they are the same then there is no mixing in the thermodynamic sense.
Gibbs himself was clearly aware of the physics here, and he did not say that he saw any paradox in it. The "paradox" is the work of textbook writers.
Books
- Adkins, C.J. (1968/1975). Equilibrium Thermodynamics, second edition, McGraw-Hill, London, ISBN 0-07-084057-1.
- Atkins, P.W., de Paula, J. (2006). Atkins' Physical Chemistry, eighth edition, W.H. Freeman, New York, ISBN 978-0716787594.
- Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics, New York, ISBN 0-88318-797-3.


