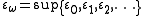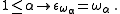Epsilon nought
Encyclopedia
In mathematics
, the epsilon numbers are a collection of transfinite number
s whose defining property is that they are fixed point
s of an exponential map
. Consequently, they are not reachable from 0 via a finite series of applications of the chosen exponential map and of "weaker" operations like addition and multiplication. The original epsilon numbers were introduced by Georg Cantor
in the context of ordinal arithmetic
; they are the ordinal numbers ε that satisfy the equation
,
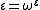in which ω is the smallest transfinite ordinal. Any solution to this equation has Cantor normal form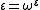
.
The least such ordinal is ε0 , which can be viewed as the "limit" obtained by transfinite recursion from a sequence of smaller limit ordinals:
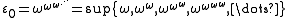
Larger ordinal fixed points of the exponential map are indexed by ordinal subscripts, resulting in ε1, ε2, ... εω, εω+1, ...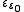
, ... 
, ... 
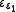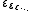, .... The ordinal ε0 is still countable, as is any epsilon number whose index is countable (there exist uncountable ordinals, and uncountable epsilon numbers whose index is an uncountable ordinal).
The smallest epsilon number ε0 is very important in many induction
proofs, because for many purposes, transfinite induction
is only required up to ε0 (as in Gentzen's consistency proof
and the proof of Goodstein's theorem
). Its use by Gentzen to prove the consistency of Peano arithmetic, along with Gödel's second incompleteness theorem, show that Peano arithmetic cannot prove the well-foundedness of this ordering (it is in fact the least ordinal with this property, and as such, in proof-theoretic ordinal analysis
, is used as a measure of the strength of the theory of Peano arithmetic).
Many larger epsilon numbers can be defined using the Veblen function
.
A more general class of epsilon numbers has been identified by John Horton Conway
and Donald Knuth
in the surreal number
system, consisting of all surreals that are fixed points of the base ω exponential map x → ωx.
From this definition, it follows that for any fixed ordinal α>1, the mapping
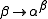is a normal function
, so it has arbitrarily large fixed points
by the fixed-point lemma for normal functions
. When
, these fixed points are precisely the ordinal epsilon numbers. The smallest of these, ε₀, is the supremum of the sequence
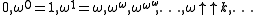
in which every element is the image of its predecessor under the mapping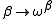
. (The general term is given using Knuth's up-arrow notation
; the
operator is equivalent to tetration
.) Just as ωω is defined as the supremum of { ωk } for natural numbers k, the smallest ordinal epsilon number ε₀ may also be denoted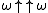
; this notation is much less common than ε₀.
The next epsilon number after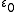
is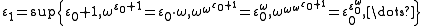
,
in which the sequence is again constructed by repeated base ω exponentiation but starts at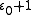
instead of at 0. (Note that 
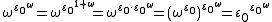.) A different sequence with the same supremum is obtained by starting from 0 and exponentiating with base ε₀ instead:
,
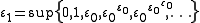The epsilon number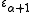
indexed by any successor ordinal α+1 is constructed similarly, by base ω exponentiation starting from 
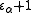(or by base 
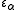exponentiation starting from 0).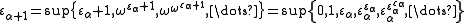
An epsilon number indexed by a limit ordinal α is constructed differently. The number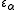
is the supremum of the set of epsilon numbers 
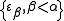. The first such number is 
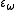. Whether or not the index α is a limit ordinal, 
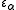is a fixed point not only of base ω exponentiation but also of base γ exponentiation for all ordinals 
.
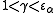Since the epsilon numbers are an unbounded subclass of the ordinal numbers, they are enumerated using the ordinal numbers themselves. For any ordinal number
, 
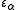is the least epsilon number (fixed point of the exponential map) not already in the set 
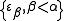. It might appear that this is the non-constructive equivalent of the constructive definition using iterated exponentiation; but the two definitions are equally non-constructive at steps indexed by limit ordinals, which represent transfinite recursion of a higher order than taking the supremum of an exponential series.
The following facts about epsilon numbers are very straightforward to prove:
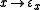form a normal function, whose fixed points form a normal function, whose …; this is known as the Veblen hierarchy
(the Veblen functions with base φ0(α)=ωα). In the notation of the Veblen hierarchy, the epsilon mapping is φ1, and its fixed points are enumerated by φ2.
Continuing in this vein, one can define maps φα for progressively larger ordinals α (including, by this rarefied form of transfinite recursion, limit ordinals), with progressively larger least fixed points φα+1(0). The least ordinal not reachable from 0 by this procedure—i. e., the least ordinal α for which φα(0)=α, or equivalently the first fixed point of the map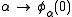
—is the Feferman–Schütte ordinal
Γ0. In a set theory where such an ordinal can be proven to exist, one has a map Γ that enumerates the fixed points Γ0, Γ1, Γ2, ... of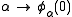
; these are all still epsilon numbers, as they lie in the image of φβ for every β≤Γ0, including of the map φ1 that enumerates epsilon numbers.
, the classic exposition on surreal number
s, John Horton Conway
provided a number of examples of concepts that had natural extensions from the ordinals to the surreals. One such function is the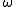
-map 
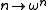; this mapping generalises naturally to include all surreal numbers in its domain, which in turn provides a natural generalisation of the Cantor normal form for surreal numbers.
It is natural to consider any fixed point of this expanded map to be an epsilon number, whether or not it happens to be strictly an ordinal number. Some examples of non-ordinal epsilon numbers are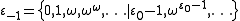
and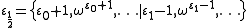
.
There is a natural way to define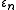
for every surreal number n, and the map remains order-preserving. Conway goes on to define a broader class of "irreducible" surreal numbers that includes the epsilon numbers as a particularly-interesting subclass.
The surreal epsilon numbers form a subclass of the class of surreals that are fixed points of the base 2 exponential map x → 2x (or equivalently of the base y exponential map for any other finite base y > 1). This latter class is the most general idea of "epsilon number" (exponential fixed point), in the same sense in which the surreals are the most general kind of "number" (ordered field); but it differs from the ordinal epsilon numbers in critical respects (beginning with the fact that ω is a fixed point of x → 2x but not of x → ωx). The fixed points of x → 2x can also be indexed by the surreals; for every surreal x with birthday α, there is a fixed point F(x) with birthday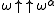
.
If the birthday of x is a successor ordinal α+1, Sα contains either a greatest element y such that y<x or a least element z such that z>x (or both). The fixed point F(x) is the exponential attractor of F(y)+1 and/or F(z)−1, i. e., the surreal number obtained by transfinite recursion from a series formed by iterated base 2 exponentiation starting at F(y)+1 or F(z)−1. (More precisely, iterated exponentiation attracts any non-fixed-point surreal number to one of the gaps above the reals in the surreal number system. The exponential attractor is the result of transfinite recursion "into the gap", i. e., the simplest surreal number lying beyond the gap.) As usual, the case where the birthday of x is a limit ordinal α is handled using Conway cuts in the transfinite union of previous generations.
The unique fixed point of x → 2x with birthday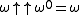
is ω itself, which we may label F(0). The two fixed points with birthday 
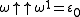are 
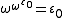and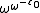 
(the smallest infinite number in generation ε₀); they are the exponential attractors of ω+1 and ω−1 respectively, and may be labeled F(1) and F(−1). The largest and smallest infinite numbers in generation ε1 are F(2)=ε1 and F(−2) respectively; Conway's ε−1 also appears in generation ε1 as F(1/2), and his 
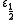appears in generation ε2 as F(3/2).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the epsilon numbers are a collection of transfinite number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s whose defining property is that they are fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of an exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
. Consequently, they are not reachable from 0 via a finite series of applications of the chosen exponential map and of "weaker" operations like addition and multiplication. The original epsilon numbers were introduced by Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
in the context of ordinal arithmetic
Ordinal arithmetic
In the mathematical field of set theory, ordinal arithmetic describes the three usual operations on ordinal numbers: addition, multiplication, and exponentiation. Each can be defined in essentially two different ways: either by constructing an explicit well-ordered set which represents the...
; they are the ordinal numbers ε that satisfy the equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
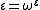,in which ω is the smallest transfinite ordinal. Any solution to this equation has Cantor normal form
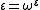.The least such ordinal is ε0 , which can be viewed as the "limit" obtained by transfinite recursion from a sequence of smaller limit ordinals:
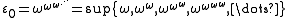
Larger ordinal fixed points of the exponential map are indexed by ordinal subscripts, resulting in ε1, ε2, ... εω, εω+1, ...
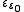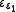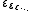, ... , ... , .... The ordinal ε0 is still countable, as is any epsilon number whose index is countable (there exist uncountable ordinals, and uncountable epsilon numbers whose index is an uncountable ordinal).The smallest epsilon number ε0 is very important in many induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
proofs, because for many purposes, transfinite induction
Transfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
is only required up to ε0 (as in Gentzen's consistency proof
Gentzen's consistency proof
Gentzen's consistency proof is a result of proof theory in mathematical logic. It "reduces" the consistency of a simplified part of mathematics, not to something that could be proved , but to clarified logical principles.-Gentzen's theorem:In 1936 Gerhard Gentzen proved the consistency of...
and the proof of Goodstein's theorem
Goodstein's theorem
In mathematical logic, Goodstein's theorem is a statement about the natural numbers, made by Reuben Goodstein, which states that every Goodstein sequence eventually terminates at 0. showed that it is unprovable in Peano arithmetic...
). Its use by Gentzen to prove the consistency of Peano arithmetic, along with Gödel's second incompleteness theorem, show that Peano arithmetic cannot prove the well-foundedness of this ordering (it is in fact the least ordinal with this property, and as such, in proof-theoretic ordinal analysis
Ordinal analysis
In proof theory, ordinal analysis assigns ordinals to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε0.-Definition:Ordinal...
, is used as a measure of the strength of the theory of Peano arithmetic).
Many larger epsilon numbers can be defined using the Veblen function
Veblen function
In mathematics, the Veblen functions are a hierarchy of normal functions , introduced by Oswald Veblen in...
.
A more general class of epsilon numbers has been identified by John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
and Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
in the surreal number
Surreal number
In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number...
system, consisting of all surreals that are fixed points of the base ω exponential map x → ωx.
Ordinal ε numbers
The standard definition of ordinal exponentiation with base α is: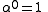
,
,
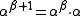for limit 
.
From this definition, it follows that for any fixed ordinal α>1, the mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
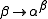is a normal functionNormal function
In axiomatic set theory, a function f : Ord → Ord is called normal iff it is continuous and strictly monotonically increasing. This is equivalent to the following two conditions:...
, so it has arbitrarily large fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
by the fixed-point lemma for normal functions
Fixed-point lemma for normal functions
The fixed-point lemma for normal functions is a basic result in axiomatic set theory stating that any normal function has arbitrarily large fixed points...
. When
, these fixed points are precisely the ordinal epsilon numbers. The smallest of these, ε₀, is the supremum of the sequence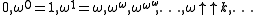in which every element is the image of its predecessor under the mapping
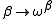. (The general term is given using Knuth's up-arrow notationKnuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
; the
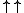operator is equivalent to tetrationTetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
.) Just as ωω is defined as the supremum of { ωk } for natural numbers k, the smallest ordinal epsilon number ε₀ may also be denoted
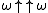; this notation is much less common than ε₀.The next epsilon number after
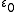is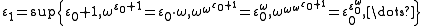,in which the sequence is again constructed by repeated base ω exponentiation but starts at
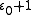instead of at 0. (Note that 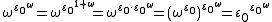.) A different sequence with the same supremum is obtained by starting from 0 and exponentiating with base ε₀ instead: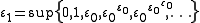,The epsilon number
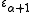indexed by any successor ordinal α+1 is constructed similarly, by base ω exponentiation starting from 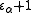(or by base 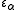exponentiation starting from 0).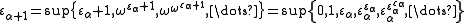An epsilon number indexed by a limit ordinal α is constructed differently. The number
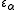is the supremum of the set of epsilon numbers 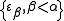. The first such number is 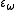. Whether or not the index α is a limit ordinal, 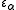is a fixed point not only of base ω exponentiation but also of base γ exponentiation for all ordinals 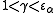.Since the epsilon numbers are an unbounded subclass of the ordinal numbers, they are enumerated using the ordinal numbers themselves. For any ordinal number
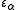, is the least epsilon number (fixed point of the exponential map) not already in the set 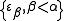. It might appear that this is the non-constructive equivalent of the constructive definition using iterated exponentiation; but the two definitions are equally non-constructive at steps indexed by limit ordinals, which represent transfinite recursion of a higher order than taking the supremum of an exponential series.The following facts about epsilon numbers are very straightforward to prove:
- Although it is quite a large number,
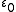is still countable, being a countable union of countable ordinals; in fact, 
is countable if and only if 
is countable. - The union (or supremum) of any nonempty set of epsilon numbers is an epsilon number; so for instance
-
- is an epsilon number. Thus, the mapping
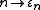is a normal function.
- Every uncountableUncountable setIn mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
cardinal numberCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
is an epsilon number.
- Every uncountable
Veblen hierarchy
The fixed points of the "epsilon mapping"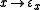 form a normal function, whose fixed points form a normal function, whose …; this is known as the Veblen hierarchyVeblen function
In mathematics, the Veblen functions are a hierarchy of normal functions , introduced by Oswald Veblen in...
(the Veblen functions with base φ0(α)=ωα). In the notation of the Veblen hierarchy, the epsilon mapping is φ1, and its fixed points are enumerated by φ2.
Continuing in this vein, one can define maps φα for progressively larger ordinals α (including, by this rarefied form of transfinite recursion, limit ordinals), with progressively larger least fixed points φα+1(0). The least ordinal not reachable from 0 by this procedure—i. e., the least ordinal α for which φα(0)=α, or equivalently the first fixed point of the map
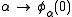—is the Feferman–Schütte ordinalFeferman–Schütte ordinal
In mathematics, the Feferman–Schütte ordinal Γ0 is a large countable ordinal.It is the proof theoretic ordinal of several mathematical theories, such as arithmetical transfinite recursion.It is named after Solomon Feferman and Kurt Schütte....
Γ0. In a set theory where such an ordinal can be proven to exist, one has a map Γ that enumerates the fixed points Γ0, Γ1, Γ2, ... of
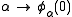; these are all still epsilon numbers, as they lie in the image of φβ for every β≤Γ0, including of the map φ1 that enumerates epsilon numbers.Surreal ε numbers
In On Numbers and GamesOn Numbers and Games
On Numbers and Games is a mathematics book by John Horton Conway. The book is a serious mathematics book, written by a pre-eminent mathematician, and is directed at other mathematicians...
, the classic exposition on surreal number
Surreal number
In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number...
s, John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
provided a number of examples of concepts that had natural extensions from the ordinals to the surreals. One such function is the
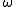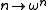-map ; this mapping generalises naturally to include all surreal numbers in its domain, which in turn provides a natural generalisation of the Cantor normal form for surreal numbers.It is natural to consider any fixed point of this expanded map to be an epsilon number, whether or not it happens to be strictly an ordinal number. Some examples of non-ordinal epsilon numbers are
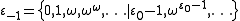
and
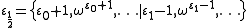.There is a natural way to define
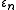for every surreal number n, and the map remains order-preserving. Conway goes on to define a broader class of "irreducible" surreal numbers that includes the epsilon numbers as a particularly-interesting subclass.The surreal epsilon numbers form a subclass of the class of surreals that are fixed points of the base 2 exponential map x → 2x (or equivalently of the base y exponential map for any other finite base y > 1). This latter class is the most general idea of "epsilon number" (exponential fixed point), in the same sense in which the surreals are the most general kind of "number" (ordered field); but it differs from the ordinal epsilon numbers in critical respects (beginning with the fact that ω is a fixed point of x → 2x but not of x → ωx). The fixed points of x → 2x can also be indexed by the surreals; for every surreal x with birthday α, there is a fixed point F(x) with birthday
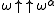.If the birthday of x is a successor ordinal α+1, Sα contains either a greatest element y such that y<x or a least element z such that z>x (or both). The fixed point F(x) is the exponential attractor of F(y)+1 and/or F(z)−1, i. e., the surreal number obtained by transfinite recursion from a series formed by iterated base 2 exponentiation starting at F(y)+1 or F(z)−1. (More precisely, iterated exponentiation attracts any non-fixed-point surreal number to one of the gaps above the reals in the surreal number system. The exponential attractor is the result of transfinite recursion "into the gap", i. e., the simplest surreal number lying beyond the gap.) As usual, the case where the birthday of x is a limit ordinal α is handled using Conway cuts in the transfinite union of previous generations.
The unique fixed point of x → 2x with birthday
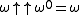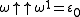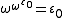is ω itself, which we may label F(0). The two fixed points with birthday are and 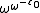(the smallest infinite number in generation ε₀); they are the exponential attractors of ω+1 and ω−1 respectively, and may be labeled F(1) and F(−1). The largest and smallest infinite numbers in generation ε1 are F(2)=ε1 and F(−2) respectively; Conway's ε−1 also appears in generation ε1 as F(1/2), and his 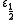appears in generation ε2 as F(3/2).