Ordinal analysis
Encyclopedia
In proof theory
, ordinal analysis assigns ordinals
(often large countable ordinals) to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen
in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε0.
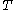is the smallest recursive ordinal that the theory cannot prove is well founded
— the supremum of all ordinals
for which there exists a notation 
in Kleene's sense such that 
proves that 
is an ordinal notation
. Equivalently, it is the supremum of all ordinals
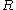such that there exists a recursive relation
on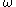 
(the set of natural numbers) which well-order
s it with ordinal
and such that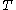 
proves transfinite induction
of arithmetical statements for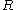
.
The existence of any recursive ordinal which the theory fails to prove is well ordered follows from the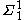
bounding theorem, as the set of natural numbers which an effective theory proves to be ordinal notations is a 
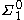set (see Hyperarithmetical theory
). Thus the proof theoretic ordinal of a theory will always be a countable ordinal less than the Church-Kleene ordinal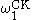
.
In practice, the proof theoretic ordinal of a theory is a good measure of the strength of a theory. If theories have the same proof theoretic ordinal they are often equiconsistent
, and if one theory has a larger proof theoretic ordinal than another it can often prove the consistency of the second theory.
suggests that much "ordinary" mathematics can be proved in weak systems having this as their proof-theoretic ordinal.
Most theories capable of describing the power set of the natural numbers have proof theoretic ordinals
that are so large that no explicit combinatorial description has yet been given. This includes second order arithmetic and set theories with powersets. (Kripke-Platek set theory mentioned above is a weak set theory without power sets.)
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
, ordinal analysis assigns ordinals
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
(often large countable ordinals) to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen
Gerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε0.
Definition
Ordinal analysis concerns true, effective (recursive) theories that can interpret a sufficient portion of arithmetic to make statements about ordinal notations. The proof theoretic ordinal of such a theory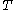 is the smallest recursive ordinal that the theory cannot prove is well foundedWell-founded relation
In mathematics, a binary relation, R, is well-founded on a class X if and only if every non-empty subset of X has a minimal element with respect to R; that is, for every non-empty subset S of X, there is an element m of S such that for every element s of S, the pair is not in R:\forall S...
— the supremum of all ordinals
for which there exists a notation in Kleene's sense such that proves that is an ordinal notationOrdinal notation
In mathematical logic and set theory, an ordinal notation is a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language....
. Equivalently, it is the supremum of all ordinals
such that there exists a recursive relationComputable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
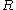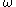on (the set of natural numbers) which well-orderWell-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
s it with ordinal
and such that 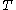proves transfinite inductionTransfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
of arithmetical statements for
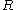.The existence of any recursive ordinal which the theory fails to prove is well ordered follows from the
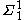bounding theorem, as the set of natural numbers which an effective theory proves to be ordinal notations is a 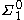set (see Hyperarithmetical theoryHyperarithmetical theory
In recursion theory, hyperarithmetic theory is a generalization of Turing computability. It has close connections with definability in second-order arithmetic and with weak systems of set theory such as Kripke–Platek set theory...
). Thus the proof theoretic ordinal of a theory will always be a countable ordinal less than the Church-Kleene ordinal
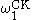.In practice, the proof theoretic ordinal of a theory is a good measure of the strength of a theory. If theories have the same proof theoretic ordinal they are often equiconsistent
Equiconsistency
In mathematical logic, two theories are equiconsistent if, roughly speaking, they are "as consistent as each other".It is not in general possible to prove the absolute consistency of a theory T...
, and if one theory has a larger proof theoretic ordinal than another it can often prove the consistency of the second theory.
Theories with proof theoretic ordinal ω2
- RFA, rudimentary function arithmetic.
- IΔ0, arithmetic with induction on Δ0-predicates without any axiom asserting that exponentiation is total.
Theories with proof theoretic ordinal ω3
Friedman's grand conjectureGrand conjecture
In proof theory, a branch of mathematical logic, elementary function arithmetic or exponential function arithmetic is the system of arithmetic with the usual elementary properties of 0, 1, +, ×, xy, together with induction for formulas with bounded quantifiers.EFA is a...
suggests that much "ordinary" mathematics can be proved in weak systems having this as their proof-theoretic ordinal.
- EFA, elementary function arithmetic.
- IΔ0 + exp, arithmetic with induction on Δ0-predicates augmented by an axiom asserting that exponentiation is total.
- RCA, a second order form of EFA sometimes used in reverse mathematicsReverse mathematicsReverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...
. - WKL, a second order form of EFA sometimes used in reverse mathematicsReverse mathematicsReverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...
.
Theories with proof theoretic ordinal ωn
- IΔ0 or EFA augmented by an axiom ensuring that each element of the n-th level
of the Grzegorczyk hierarchyGrzegorczyk hierarchyThe Grzegorczyk hierarchy , named after the Polish logician Andrzej Grzegorczyk, is a hierarchy of functions used in computability theory . Every function in the Grzegorczyk hierarchy is a primitive recursive function, and every primitive recursive function appears in the hierarchy at some level...
is total.
Theories with proof theoretic ordinal ωω
- RCA0, recursive comprehension.
- WKL0, weak König's lemma.
- PRA, primitive recursive arithmeticPrimitive recursive arithmeticPrimitive recursive arithmetic, or PRA, is a quantifier-free formalization of the natural numbers. It was first proposed by Skolem as a formalization of his finitist conception of the foundations of arithmetic, and it is widely agreed that all reasoning of PRA is finitist...
. - IΣ1, arithmetic with induction on Σ1-predicates.
Theories with proof theoretic ordinal ε0
- PA, Peano arithmetic (shownGentzen's consistency proofGentzen's consistency proof is a result of proof theory in mathematical logic. It "reduces" the consistency of a simplified part of mathematics, not to something that could be proved , but to clarified logical principles.-Gentzen's theorem:In 1936 Gerhard Gentzen proved the consistency of...
by Gentzen using cut elimination). - ACA0, arithmetical comprehension.
Theories with proof theoretic ordinal the Feferman-Schütte ordinal Γ0
This ordinal is sometimes considered to be the upper limit for "predicative" theories.- ATR0, arithmetical transfinite recursion.
- Martin-Löf type theory.
Theories with proof theoretic ordinal the Bachmann-Howard ordinal
- ID1, the theory of inductive definitions.
- KP, Kripke-Platek set theory with the axiom of infinityAxiom of infinityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
. - CZF, Aczel's constructive Zermelo-Fraenkel set theory.
Theories with larger proof theoretic ordinals
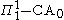, Π11 comprehension has a rather large proof theoretic ordinal, which was described by Takeuti in terms of "ordinal diagrams", and which is bounded by ψ0(Ωω)Psi0(Omega omega)In mathematics, Ψ0 is a large countable ordinal that is used to measure the proof-theoretic strength of some mathematical systems. In particular, it is the proof theoretic ordinal of the subsystem \Pi_1^1-CA0 of second-order arithmetic; this is one of the "big five" subsystems studied in reverse...
in Buchholz's notation. It is also the ordinal of
, the theory of finitely iterated inductive definitions.- KPM, an extension of Kripke-Platek set theory based on a Mahlo cardinalMahlo cardinalIn mathematics, a Mahlo cardinal is a certain kind of large cardinal number. Mahlo cardinals were first described by . As with all large cardinals, none of these varieties of Mahlo cardinals can be proved to exist by ZFC ....
, has a very large proof theoretic ordinal, which was described by .
Most theories capable of describing the power set of the natural numbers have proof theoretic ordinals
that are so large that no explicit combinatorial description has yet been given. This includes second order arithmetic and set theories with powersets. (Kripke-Platek set theory mentioned above is a weak set theory without power sets.)
See also
- EquiconsistencyEquiconsistencyIn mathematical logic, two theories are equiconsistent if, roughly speaking, they are "as consistent as each other".It is not in general possible to prove the absolute consistency of a theory T...
- Large cardinal propertyLarge cardinal propertyIn the mathematical field of set theory, a large cardinal property is a certain kind of property of transfinite cardinal numbers. Cardinals with such properties are, as the name suggests, generally very "large"...
- Feferman–Schütte ordinalFeferman–Schütte ordinalIn mathematics, the Feferman–Schütte ordinal Γ0 is a large countable ordinal.It is the proof theoretic ordinal of several mathematical theories, such as arithmetical transfinite recursion.It is named after Solomon Feferman and Kurt Schütte....
- Bachmann–Howard ordinalBachmann–Howard ordinalIn mathematics, the Bachmann–Howard ordinal is a large countable ordinal.It is the proof theoretic ordinal of several mathematical theories, such as Kripke–Platek set theory and the system CZF of constructive set theory.It is named after William Alvin Howard and Heinz Bachmann.-Definition:The...