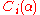Psi0(Omega omega)
Encyclopedia
In mathematics, Ψ0 is a large countable ordinal
that is used to measure the proof-theoretic strength of some mathematical systems. In particular, it is the proof theoretic ordinal of the subsystem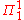
-CA0 of second-order arithmetic
; this is one of the "big five" subsystems studied in reverse mathematics
(Simpson 1999).
Large countable ordinal
In the mathematical discipline of set theory, there are many ways of describing specific countable ordinals. The smallest ones can be usefully and non-circularly expressed in terms of their Cantor normal forms. Beyond that, many ordinals of relevance to proof theory still have computable ordinal...
that is used to measure the proof-theoretic strength of some mathematical systems. In particular, it is the proof theoretic ordinal of the subsystem
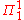-CA0 of second-order arithmeticSecond-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
; this is one of the "big five" subsystems studied in reverse mathematics
Reverse mathematics
Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...
(Simpson 1999).
Definition
-
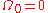, and 
for n > 0. -
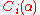is the smallest set of ordinals that contains 
for n finite, and contains all ordinals less than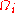 
, and is closed under ordinal addition and exponentiation, and contains 
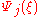if j ≥ i and 
and 
. -
is the smallest ordinal not in 