Second-order arithmetic
Encyclopedia
In mathematical logic
, second-order arithmetic is a collection of axiom
atic systems that formalize the natural number
s and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert
and Paul Bernays
in their book Grundlagen der Mathematik
. The standard axiomatization of second-order arithmetic is denoted Z2.
Second-order arithmetic includes, but is significantly stronger than, its first-order counterpart Peano arithmetic. Unlike Peano arithmetic, second-order arithmetic allows quantification
over sets of numbers as well as numbers themselves. Because real number
s can be represented as (infinite) sets of natural numbers in well-known ways, and because second order arithmetic allows quantification
over such sets, it is possible to formalize the real number
s in second-order arithmetic. For this reason, second-order arithmetic is sometimes called “analysis
”.
Second-order arithmetic can also be seen as a weak version of set theory
in which every element is either a natural number or a set of natural numbers. Although it is much weaker than Zermelo-Fraenkel set theory, second-order arithmetic can prove essentially all of the results of classical mathematics
expressible in its language.
A subsystem of second-order arithmetic is a theory in the language of second-order arithmetic each axiom of which is a theorem of full second-order arithmetic (Z2). Such subsystems are essential to reverse mathematics
, a research program investigating how much of classical mathematics can be derived in certain weak subsystems of varying strength. Much of core mathematics can be formalized in these weak subsystems, some of which are defined below. Reverse mathematics also clarifies the extent and manner in which classical mathematics is nonconstructive.
and variables
, usually denoted by lower case letters, consists of individual
s, whose intended interpretation is as natural numbers. The other sort of variables, variously called “set variables,” “class variables,” or even “predicates” are usually denoted by upper case letters. They refer to classes/predicates/properties of individuals, and so can be thought of as sets of natural numbers. Both individuals and set variables can be quantified universally or existentially. A formula with no bound set variables (that is, no quantifiers over set variables) is called arithmetical. An arithmetical formula may have free set variables and bound individual variables.
Individual terms are formed from the constant 0, the unary function S (the successor function), and the binary operations + and · (addition and multiplication). The successor function adds 1 (=S0) to its input. The relations = (equality) and < (comparison of natural numbers) relate two individuals, whereas the relation ∈ (membership) relates an individual and a set (or class).
For example,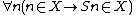
, is a well-formed formula
of second-order arithmetic that is arithmetical, has one free set variable X and one bound individual variable n (but no bound set variables, as is required of an arithmetical formula)—whereas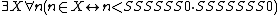
is a well-formed formula that is not arithmetical with one bound set variable X and one bound individual variable n.
then the set quantifiers range over all subsets of the range of the number variables. If second-order arithmetic is formalized using the semantics of first-order logic
then any model includes a domain for the set variables to range over, and this domain may be a proper subset of the full powerset of the domain of number variables.
Although second-order arithmetic was originally studied using full second-order semantics, the vast majority of current research treats second-order arithmetic in first-order predicate calculus. This is because the model theory of subsystems of second-order arithmetic is more interesting in the setting of first-order logic.
, is essentially Peano arithmetic without induction. The domain of discourse
for the quantified variable
s is the natural number
s, collectively denoted by N, and including the distinguished member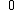
, called "zero."
The primitive functions are the unary successor function, denoted by prefix
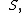, and two binary operation
s, addition
and multiplication
, denoted by infix
"+" and "
", respectively. There is also a primitive binary relation
called order, denoted by infix "<".
Axioms governing the successor function and zero:
Addition
defined recursively
:
Multiplication
defined recursively:
Axioms governing the order relation "<":
These axioms are all first order statements. That is, all variables range over the natural number
s and not sets
thereof, a fact even stronger than their being arithmetical. Moreover, there is but one existential quantifier, in axiom 3. Axioms 1 and 2, together with an axiom schema of induction
make up the usual Peano-Dedekind
definition of N. Adding to these axioms any sort of axiom schema of induction
makes redundant the axioms 3, 10, and 11.
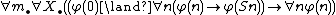
The (full) second-order induction scheme consists of all instances of this axiom, over all second-order formulas.
One particularly important instance of the induction scheme is when φ is the formula “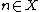
” expressing the fact that n is a member of X (X being a free set variable): in this case, the induction axiom for φ is
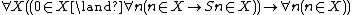
This sentence is called the second-order induction axiom.
Returning to the case where φ(n) is a formula with a free variable n and possibly other free variables, we define the comprehension axiom for φ to be:
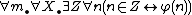
Essentially, this allows us to form the set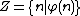
of natural numbers satisfying φ(n). There is a technical restriction that the formula φ may not contain the variable Z, for otherwise the formula 
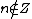would lead to the comprehension axiom
,
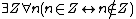which is inconsistent. This convention is assumed in the remainder of this article.
In the presence of the unrestricted comprehension scheme, the single second-order induction axiom implies each instance of the full induction scheme. Subsystems that limit comprehension in some way may offset this limitation by including part of the induction scheme. Examples of such systems are provided below.
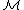of the language of second-order arithmetic consists of a set M (which forms the range of individual variables) together with a constant 0 (an element of M),
a function S from M to M, two binary operations + and · on M, a binary relation < on M, and a collection D of subsets of M, which is the range of the set variables. By omitting D we obtain a model of the language of first order arithmetic.
When D is the full powerset of M, the model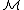
is called a full model. The use of full second-order semantics is equivalent to limiting the models of second-order arithmetic to the full models. In fact, the axioms of second-order arithmetic have only one full model. This follows from the fact that the axioms of Peano arithmetic with the second-order induction axiom have only one model under second-order semantics.
When M is the usual set of natural numbers with its usual operations,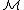
is called an ω-model. In this case we may identify the model with D, its collection of sets of naturals, because this set is enough to completely determine an ω-model.
The unique full model, which is the usual set of natural numbers with its usual structure and all its subsets, is called the intended or standard model of second-order arithmetic.
(Girard et al., 1987, pp. 122–123). Almost equivalently, system F is the theory of functionals corresponding to second-order arithmetic in a manner parallel to how Gödel's system T
corresponds to first-order arithmetic in the Dialectica interpretation
.
A subscript 0 in the name of a subsystem indicates that it includes only
a restricted portion of the full second-order induction scheme (Friedman 1976). Such a restriction lowers the proof-theoretic strength of the system significantly. For example, the system ACA0 described below is equiconsistent
with Peano arithmetic. The corresponding theory ACA, consisting of ACA0 plus the full second-order induction scheme, is stronger than Peano arithmetic.
, but not every ω-model closed under Turing jump is a model of full second-order arithmetic. We may ask whether there is a subsystem of second-order arithmetic satisfied by every ω-model that is closed under Turing jump and satisfies some other, more mild, closure conditions.
The subsystem just described is called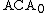
.
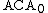is defined as the theory consisting of the basic axioms, the arithmetical comprehension axiom scheme, in other words the comprehension axiom for every arithmetical formula φ, and the ordinary second-order induction axiom; again, we could also choose to include the arithmetical induction axiom scheme, in other words the induction axiom for every arithmetical formula φ, without making a difference.
It can be seen that a collection S of subsets of ω determines an ω-model of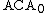
if and only if S is closed under Turing jump, Turing reducibility, and Turing join.
The subscript 0 in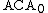
indicates that we have not included every instance of the induction axiom in this subsystem. This makes no difference when we study only ω-models, which automatically satisfy every instance of the induction axiom. It is of crucial importance, however, when we study models that are not ω-models. The system consisting of 
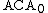plus induction for all formulas is sometimes called 
.
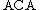The system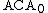
is a conservative extension of first-order arithmetic (or first-order Peano axioms), defined as the basic axioms, plus the first order induction axiom scheme (for all formulas φ involving no class variables at all, bound or otherwise), in the language of first order arithmetic (which does not permit class variables at all). In particular it has the same proof-theoretic ordinal
ε0 as first-order arithmetic, owing to the limited induction schema.
A formula is called bounded arithmetical, or Δ00, when all its quantifiers are of the form ∀n<t or ∃n<t (where n is the individual variable being quantified and t is an individual term), where
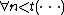
stands for
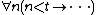
and
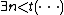
stands for
.
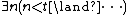A formula is called Σ01 (or sometimes Σ1), respectively Π01 (or sometimes Π1) when it of the form ∃m•(φ), respectively ∀m•(φ) where φ is a bounded arithmetical formula and m is an individual variable (that is free in φ). More generally, a formula is called Σ0n, respectively Π0n when it is obtained by adding existential, respectively universal, individual quantifiers to a Π0n−1, respectively Σ0n−1 formula (and Σ00 and Π00 are all equivalent to Δ00). Note that by construction all these formulas are arithmetical (no class variables are ever bound) and, in fact, by putting the formula in Skolem prenex form one can see that every arithmetical formula is equivalent to a Σ0n or Π0n formula for all large enough n.
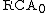is an even weaker system than 
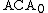and is often used as the base system in reverse mathematics
. It consists of: the basic axioms, the Σ01 induction scheme, and the Δ01 comprehension scheme. The former term is clear: the Σ01 induction scheme is the induction axiom for every Σ01 formula φ. The term “Δ01 comprehension” requires a little more explaining, however: there is no such thing as a Δ01 formula (the intended meaning is a formula that is both Σ01 and Π01), but we are instead postulating the comprehension axiom for every Σ01 formula subject to the condition that it is equivalent to a Π01 formula, in other words, for every Σ01 formula φ and every Π01 formula ψ we postulate
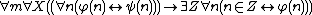
The set of first-order consequences of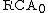
is the same as those of the subsystem IΣ1 of Peano arithmetic in which induction is restricted to Σ01 formulas. In turn, IΣ1 is conservative over primitive recursive arithmetic
(PRA) for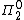
sentences. Moreover, the proof-theoretic ordinal of 
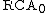is ωω, the same as that of PRA.
It can be seen that a collection S of subsets of ω determines an ω-model of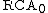
if and only if S is closed under Turing reducibility and Turing join. In particular, the collection of all computable subsets of ω gives an ω-model of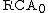
. This is the motivation behind the name of this system—if a set can be proved to exist using 
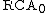, then the set is computable (i.e. recursive).
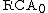is desired. One such system is defined as follows: one must first augment the language of arithmetic with an exponential function (in stronger systems the exponential can be defined in terms of addition and multiplication by the usual trick, but when the system becomes too weak this is no longer possible) and the basic axioms by the obvious axioms defining exponentiation inductively from multiplication; then the system consists of the (enriched) basic axioms, plus Δ01 comprehension plus Δ00 induction.
It is not too hard to see that over a not too weak system, any formula of second-order arithmetic is equivalent to a Σ1n or Π1n formula for all large enough n. The system Π11-comprehension is the system consisting of the basic axioms, plus the ordinary second-order induction axiom and the comprehension axiom for every Π11 formula φ. It is an easy exercise to show that this is actually equivalent to Σ11-comprehension (on the other hand, Δ11-comprehension, defined by the same trick as introduced earlier for Δ01 comprehension, is actually weaker).
s or rational number
s are first-class citizens in the same manner as natural numbers. Functions
between these sets can be encoded as sets of pairs, and hence as subset
s of the natural numbers, without difficulty. Real number
s can be defined as Cauchy sequence
s of rational number
s, but for technical reasons not discussed here, it is preferable (in the weak axiom systems above) to constrain the convergence rate (say by requiring that the distance between the n-th and (n+1)-th term be less than 2−n). These systems cannot speak of real functions, or subsets of the reals. Nevertheless, continuous
real functions are legitimate objects of study, since they are defined by their values on the rationals. Moreover, a related trick makes it possible to speak of open subsets of the reals. Even Borel set
s of reals can be coded in the language of second-order arithmetic, although doing so is a bit tricky.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, second-order arithmetic is a collection of axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
atic systems that formalize the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
and Paul Bernays
Paul Bernays
Paul Isaac Bernays was a Swiss mathematician, who made significant contributions to mathematical logic, axiomatic set theory, and the philosophy of mathematics. He was an assistant to, and close collaborator of, David Hilbert.-Biography:Bernays spent his childhood in Berlin. Bernays attended the...
in their book Grundlagen der Mathematik
Grundlagen der Mathematik
Grundlagen der Mathematik is a 2-volume work by David Hilbert and Paul Bernays describing Hilbert's approach to the foundations of mathematics...
. The standard axiomatization of second-order arithmetic is denoted Z2.
Second-order arithmetic includes, but is significantly stronger than, its first-order counterpart Peano arithmetic. Unlike Peano arithmetic, second-order arithmetic allows quantification
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
over sets of numbers as well as numbers themselves. Because real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s can be represented as (infinite) sets of natural numbers in well-known ways, and because second order arithmetic allows quantification
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
over such sets, it is possible to formalize the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s in second-order arithmetic. For this reason, second-order arithmetic is sometimes called “analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
”.
Second-order arithmetic can also be seen as a weak version of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
in which every element is either a natural number or a set of natural numbers. Although it is much weaker than Zermelo-Fraenkel set theory, second-order arithmetic can prove essentially all of the results of classical mathematics
Classical mathematics
In the foundations of mathematics, classical mathematics refers generally to the mainstream approach to mathematics, which is based on classical logic and ZFC set theory. It stands in contrast to other types of mathematics such as constructive mathematics or predicative mathematics; theories other...
expressible in its language.
A subsystem of second-order arithmetic is a theory in the language of second-order arithmetic each axiom of which is a theorem of full second-order arithmetic (Z2). Such subsystems are essential to reverse mathematics
Reverse mathematics
Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...
, a research program investigating how much of classical mathematics can be derived in certain weak subsystems of varying strength. Much of core mathematics can be formalized in these weak subsystems, some of which are defined below. Reverse mathematics also clarifies the extent and manner in which classical mathematics is nonconstructive.
Syntax
The language of second-order arithmetic is two-sorted. The first sort of termsTerm (mathematics)
A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
and variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, usually denoted by lower case letters, consists of individual
Individual
An individual is a person or any specific object or thing in a collection. Individuality is the state or quality of being an individual; a person separate from other persons and possessing his or her own needs, goals, and desires. Being self expressive...
s, whose intended interpretation is as natural numbers. The other sort of variables, variously called “set variables,” “class variables,” or even “predicates” are usually denoted by upper case letters. They refer to classes/predicates/properties of individuals, and so can be thought of as sets of natural numbers. Both individuals and set variables can be quantified universally or existentially. A formula with no bound set variables (that is, no quantifiers over set variables) is called arithmetical. An arithmetical formula may have free set variables and bound individual variables.
Individual terms are formed from the constant 0, the unary function S (the successor function), and the binary operations + and · (addition and multiplication). The successor function adds 1 (=S0) to its input. The relations = (equality) and < (comparison of natural numbers) relate two individuals, whereas the relation ∈ (membership) relates an individual and a set (or class).
For example,
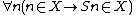, is a well-formed formulaWell-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
of second-order arithmetic that is arithmetical, has one free set variable X and one bound individual variable n (but no bound set variables, as is required of an arithmetical formula)—whereas
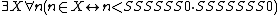is a well-formed formula that is not arithmetical with one bound set variable X and one bound individual variable n.Semantics
Several different interpretations of the quantifiers are possible. If second-order arithmetic is studied using the full semantics of second-order logicSecond-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
then the set quantifiers range over all subsets of the range of the number variables. If second-order arithmetic is formalized using the semantics of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
then any model includes a domain for the set variables to range over, and this domain may be a proper subset of the full powerset of the domain of number variables.
Although second-order arithmetic was originally studied using full second-order semantics, the vast majority of current research treats second-order arithmetic in first-order predicate calculus. This is because the model theory of subsystems of second-order arithmetic is more interesting in the setting of first-order logic.
Basic
The following axioms are known as the basic axioms, or sometimes the Robinson axioms. The resulting first-order theory, known as Robinson arithmeticRobinson arithmetic
In mathematics, Robinson arithmetic, or Q, is a finitely axiomatized fragment of Peano arithmetic , first set out in R. M. Robinson . Q is essentially PA without the axiom schema of induction. Since Q is weaker than PA, it is incomplete...
, is essentially Peano arithmetic without induction. The domain of discourse
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
for the quantified variable
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
s is the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, collectively denoted by N, and including the distinguished member
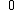, called "zero."The primitive functions are the unary successor function, denoted by prefix
Prefix
A prefix is an affix which is placed before the root of a word. Particularly in the study of languages,a prefix is also called a preformative, because it alters the form of the words to which it is affixed.Examples of prefixes:...
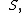, and two binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s, addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, denoted by infix
Infix
An infix is an affix inserted inside a word stem . It contrasts with adfix, a rare term for an affix attached to the end of a stem, such as a prefix or suffix.-Indonesian:...
"+" and "
", respectively. There is also a primitive binary relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
called order, denoted by infix "<".
Axioms governing the successor function and zero:
- 1.
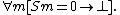(“the successor of a natural number is never zero”)
- 2.
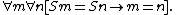(“the successor function is injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
”)
- 3.
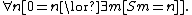(“every natural number is zero or a successor”)
Addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
defined recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
:
- 4.
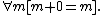
- 5.
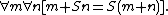
Multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
defined recursively:
- 6.
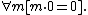
- 7.
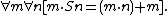
Axioms governing the order relation "<":
- 8.
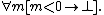(“no natural number is smaller than zero”)
- 9.
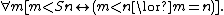
- 10.
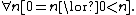(“every natural number is zero or bigger than zero”)
- 11.
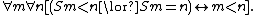
These axioms are all first order statements. That is, all variables range over the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s and not sets
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
thereof, a fact even stronger than their being arithmetical. Moreover, there is but one existential quantifier, in axiom 3. Axioms 1 and 2, together with an axiom schema of induction
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
make up the usual Peano-Dedekind
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
definition of N. Adding to these axioms any sort of axiom schema of induction
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
makes redundant the axioms 3, 10, and 11.
Induction and comprehension schema
If φ(n) is a formula of second-order arithmetic with a free number variable n and possible other free number or set variables (written m• and X•), the induction axiom for φ is the axiom: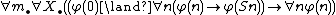The (full) second-order induction scheme consists of all instances of this axiom, over all second-order formulas.
One particularly important instance of the induction scheme is when φ is the formula “
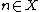” expressing the fact that n is a member of X (X being a free set variable): in this case, the induction axiom for φ is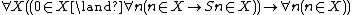This sentence is called the second-order induction axiom.
Returning to the case where φ(n) is a formula with a free variable n and possibly other free variables, we define the comprehension axiom for φ to be:
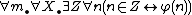
Essentially, this allows us to form the set
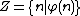of natural numbers satisfying φ(n). There is a technical restriction that the formula φ may not contain the variable Z, for otherwise the formula 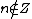would lead to the comprehension axiom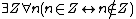,which is inconsistent. This convention is assumed in the remainder of this article.
The full system
The formal theory of second-order arithmetic (in the language of second-order arithmetic) consists of the basic axioms, the comprehension axiom for every formula φ, (arithmetic or otherwise) and the second-order induction axiom. This theory is sometimes called full second order arithmetic to distinguish it from its subsystems, defined below. Second-order semantics eliminates the need for the comprehension axiom, because these semantics imply that every possible set exists.In the presence of the unrestricted comprehension scheme, the single second-order induction axiom implies each instance of the full induction scheme. Subsystems that limit comprehension in some way may offset this limitation by including part of the induction scheme. Examples of such systems are provided below.
Models of second-order arithmetic
Recall that we view second-order arithmetic as a theory in first-order predicate calculus. Thus a model of the language of second-order arithmetic consists of a set M (which forms the range of individual variables) together with a constant 0 (an element of M),a function S from M to M, two binary operations + and · on M, a binary relation < on M, and a collection D of subsets of M, which is the range of the set variables. By omitting D we obtain a model of the language of first order arithmetic.
When D is the full powerset of M, the model
is called a full model. The use of full second-order semantics is equivalent to limiting the models of second-order arithmetic to the full models. In fact, the axioms of second-order arithmetic have only one full model. This follows from the fact that the axioms of Peano arithmetic with the second-order induction axiom have only one model under second-order semantics.When M is the usual set of natural numbers with its usual operations,
is called an ω-model. In this case we may identify the model with D, its collection of sets of naturals, because this set is enough to completely determine an ω-model.The unique full model, which is the usual set of natural numbers with its usual structure and all its subsets, is called the intended or standard model of second-order arithmetic.
Definable functions of second-order arithmetic
The first-order functions that are provably total in second-order arithmetic are precisely the same as those representable in system FSystem F
System F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...
(Girard et al., 1987, pp. 122–123). Almost equivalently, system F is the theory of functionals corresponding to second-order arithmetic in a manner parallel to how Gödel's system T
System T
In mathematics, System T can refer to:* A theory of arithmetic in all finite types use in Gödel's Dialectica interpretation* An axiom system of modal logic...
corresponds to first-order arithmetic in the Dialectica interpretation
Dialectica interpretation
In proof theory, the Dialectica interpretation is a proof interpretation of intuitionistic arithmetic into a finite type extension of primitive recursive arithmetic, the so-called System T. It was developed by Kurt Gödel to provide a consistency proof of arithmetic...
.
Subsystems of second-order arithmetic
There are many named subsystems of second-order arithmetic.A subscript 0 in the name of a subsystem indicates that it includes only
a restricted portion of the full second-order induction scheme (Friedman 1976). Such a restriction lowers the proof-theoretic strength of the system significantly. For example, the system ACA0 described below is equiconsistent
Equiconsistency
In mathematical logic, two theories are equiconsistent if, roughly speaking, they are "as consistent as each other".It is not in general possible to prove the absolute consistency of a theory T...
with Peano arithmetic. The corresponding theory ACA, consisting of ACA0 plus the full second-order induction scheme, is stronger than Peano arithmetic.
Arithmetical comprehension
Many of the well-studied subsystems are related to closure properties of models. For example, it can be shown that every ω-model of full second-order arithmetic is closed under Turing jumpTuring jump
In computability theory, the Turing jump or Turing jump operator, named for Alan Turing, is an operation that assigns to each decision problem a successively harder decision problem with the property that is not decidable by an oracle machine with an oracle for .The operator is called a jump...
, but not every ω-model closed under Turing jump is a model of full second-order arithmetic. We may ask whether there is a subsystem of second-order arithmetic satisfied by every ω-model that is closed under Turing jump and satisfies some other, more mild, closure conditions.
The subsystem just described is called
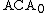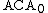. is defined as the theory consisting of the basic axioms, the arithmetical comprehension axiom scheme, in other words the comprehension axiom for every arithmetical formula φ, and the ordinary second-order induction axiom; again, we could also choose to include the arithmetical induction axiom scheme, in other words the induction axiom for every arithmetical formula φ, without making a difference.It can be seen that a collection S of subsets of ω determines an ω-model of
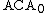if and only if S is closed under Turing jump, Turing reducibility, and Turing join.The subscript 0 in
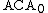indicates that we have not included every instance of the induction axiom in this subsystem. This makes no difference when we study only ω-models, which automatically satisfy every instance of the induction axiom. It is of crucial importance, however, when we study models that are not ω-models. The system consisting of 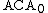plus induction for all formulas is sometimes called 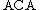.The system
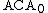is a conservative extension of first-order arithmetic (or first-order Peano axioms), defined as the basic axioms, plus the first order induction axiom scheme (for all formulas φ involving no class variables at all, bound or otherwise), in the language of first order arithmetic (which does not permit class variables at all). In particular it has the same proof-theoretic ordinalOrdinal analysis
In proof theory, ordinal analysis assigns ordinals to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε0.-Definition:Ordinal...
ε0 as first-order arithmetic, owing to the limited induction schema.
The arithmetical hierarchy for formulas
To define a second subsystem, we will need a bit more terminology.A formula is called bounded arithmetical, or Δ00, when all its quantifiers are of the form ∀n<t or ∃n<t (where n is the individual variable being quantified and t is an individual term), where
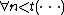
stands for
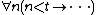
and
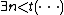
stands for
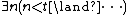.A formula is called Σ01 (or sometimes Σ1), respectively Π01 (or sometimes Π1) when it of the form ∃m•(φ), respectively ∀m•(φ) where φ is a bounded arithmetical formula and m is an individual variable (that is free in φ). More generally, a formula is called Σ0n, respectively Π0n when it is obtained by adding existential, respectively universal, individual quantifiers to a Π0n−1, respectively Σ0n−1 formula (and Σ00 and Π00 are all equivalent to Δ00). Note that by construction all these formulas are arithmetical (no class variables are ever bound) and, in fact, by putting the formula in Skolem prenex form one can see that every arithmetical formula is equivalent to a Σ0n or Π0n formula for all large enough n.
Recursive comprehension
The subsystem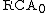 is an even weaker system than 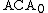and is often used as the base system in reverse mathematicsReverse mathematics
Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...
. It consists of: the basic axioms, the Σ01 induction scheme, and the Δ01 comprehension scheme. The former term is clear: the Σ01 induction scheme is the induction axiom for every Σ01 formula φ. The term “Δ01 comprehension” requires a little more explaining, however: there is no such thing as a Δ01 formula (the intended meaning is a formula that is both Σ01 and Π01), but we are instead postulating the comprehension axiom for every Σ01 formula subject to the condition that it is equivalent to a Π01 formula, in other words, for every Σ01 formula φ and every Π01 formula ψ we postulate
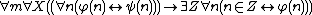
The set of first-order consequences of
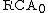is the same as those of the subsystem IΣ1 of Peano arithmetic in which induction is restricted to Σ01 formulas. In turn, IΣ1 is conservative over primitive recursive arithmeticPrimitive recursive arithmetic
Primitive recursive arithmetic, or PRA, is a quantifier-free formalization of the natural numbers. It was first proposed by Skolem as a formalization of his finitist conception of the foundations of arithmetic, and it is widely agreed that all reasoning of PRA is finitist...
(PRA) for
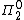sentences. Moreover, the proof-theoretic ordinal of 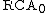is ωω, the same as that of PRA.It can be seen that a collection S of subsets of ω determines an ω-model of
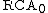
if and only if S is closed under Turing reducibility and Turing join. In particular, the collection of all computable subsets of ω gives an ω-model of
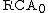. This is the motivation behind the name of this system—if a set can be proved to exist using 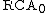, then the set is computable (i.e. recursive).Weaker systems
Sometimes an even weaker system than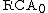 is desired. One such system is defined as follows: one must first augment the language of arithmetic with an exponential function (in stronger systems the exponential can be defined in terms of addition and multiplication by the usual trick, but when the system becomes too weak this is no longer possible) and the basic axioms by the obvious axioms defining exponentiation inductively from multiplication; then the system consists of the (enriched) basic axioms, plus Δ01 comprehension plus Δ00 induction.Stronger systems
Much as we have defined Σn and Πn (or, more accurately, Σ0n and Π0n) formulae, we can define Σ1n and Π1n formulae in the following way: a Δ10 (or Σ10 or Π10) formula is just an arithmetical formula, and a Σ1n, respectively Π1n, formula is obtained by adding existential, respectively universal, class quantifiers in front of a Π1n−1, respectively Σ1n−1.It is not too hard to see that over a not too weak system, any formula of second-order arithmetic is equivalent to a Σ1n or Π1n formula for all large enough n. The system Π11-comprehension is the system consisting of the basic axioms, plus the ordinary second-order induction axiom and the comprehension axiom for every Π11 formula φ. It is an easy exercise to show that this is actually equivalent to Σ11-comprehension (on the other hand, Δ11-comprehension, defined by the same trick as introduced earlier for Δ01 comprehension, is actually weaker).
Coding mathematics in second-order arithmetic
Second-order arithmetic allows us to speak directly (without coding) of natural numbers and sets of natural numbers. Pairs of natural numbers can be coded in the usual way as natural numbers, so arbitrary integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s or rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s are first-class citizens in the same manner as natural numbers. Functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
between these sets can be encoded as sets of pairs, and hence as subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of the natural numbers, without difficulty. Real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s can be defined as Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, but for technical reasons not discussed here, it is preferable (in the weak axiom systems above) to constrain the convergence rate (say by requiring that the distance between the n-th and (n+1)-th term be less than 2−n). These systems cannot speak of real functions, or subsets of the reals. Nevertheless, continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
real functions are legitimate objects of study, since they are defined by their values on the rationals. Moreover, a related trick makes it possible to speak of open subsets of the reals. Even Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s of reals can be coded in the language of second-order arithmetic, although doing so is a bit tricky.
See also
- Paris-Harrington theorem
- Reverse mathematicsReverse mathematicsReverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...
- Presburger arithmeticPresburger arithmeticPresburger arithmetic is the first-order theory of the natural numbers with addition, named in honor of Mojżesz Presburger, who introduced it in 1929. The signature of Presburger arithmetic contains only the addition operation and equality, omitting the multiplication operation entirely...
- Peano arithmetic
- Robinson arithmeticRobinson arithmeticIn mathematics, Robinson arithmetic, or Q, is a finitely axiomatized fragment of Peano arithmetic , first set out in R. M. Robinson . Q is essentially PA without the axiom schema of induction. Since Q is weaker than PA, it is incomplete...
- Second order logic