Large countable ordinal
Encyclopedia
In the mathematical discipline of set theory
, there are many ways of describing specific countable
ordinals
. The smallest ones can be usefully and non-circularly expressed in terms of their Cantor normal forms. Beyond that, many ordinals of relevance to proof theory
still have computable
ordinal notation
s. However, it is not possible to decide effectively whether a given putative ordinal notation is a notation or not (for reasons somewhat analogous to the unsolvability of the halting problem
); various more-concrete ways of defining ordinals that definitely have notations are available.
Since there are only countably many notations, all ordinals with notations are exhausted well below the first uncountable ordinal ω1
; their supremum
is called Church–Kleene ω1 or ω1CK (not to be confused with the first uncountable ordinal, ω1), described below. Ordinal numbers below ω1CK are the recursive ordinals (see below). Countable ordinals larger than this may still be defined, but do not have notations.
Due to the focus on countable ordinals, ordinal arithmetic
is used throughout, except where otherwise noted. The ordinals described here are not as large as the ones described in large cardinals, but they are large among those that have constructive notations (descriptions). Larger and larger ordinals can be defined, but they become more and more difficult to describe.
s (or computable ordinals) are certain countable ordinals: loosely speaking those represented by a computable function
. There are several equivalent definitions of this: the simplest is to say that a computable ordinal is the order-type of some recursive (i.e., computable) well-ordering of the natural numbers; so, essentially, an ordinal is recursive when we can present the set of smaller ordinals in such a way that a computer (Turing machine
, say) can manipulate them (and, essentially, compare them).
A different definition uses Kleene
's system of ordinal notation
s. Briefly, an ordinal notation is either the name zero (describing the ordinal 0), or the successor of an ordinal notation (describing the successor of the ordinal described by that notation), or a Turing machine (computable function) that produces an increasing sequence of ordinal notations (that describe the ordinal that is the limit of the sequence), and ordinal notations are (partially) ordered so as to make the successor of o greater than o and to make the limit greater than any term of the sequence (this order is computable; however, the set O of ordinal notations itself is highly non-recursive, owing to the impossibility of deciding whether a given Turing machine does indeed produce a sequence of notations); a recursive ordinal is then an ordinal described by some ordinal notation.
Any ordinal smaller than a recursive ordinal is itself recursive, so the set of all recursive ordinals forms a certain (countable) ordinal, the Church-Kleene ordinal (see below).
It is tempting to forget about ordinal notations, and only speak of the recursive ordinals themselves: and some statements are made about recursive ordinals which, in fact, concern the notations for these ordinals. This leads to difficulties, however, as even the smallest infinite ordinal, ω, has many notations, some of which cannot be proven to be equivalent to the obvious notation (the limit of the simplest program that enumerates all natural numbers).
s (containing arithmetic
, that is, at least a reasonable fragment of Peano arithmetic
).
Certain computable ordinals are so large that while they can be given by a certain ordinal notation o, a given formal system might not be sufficiently powerful to show that o is, indeed, an ordinal notation: the system does not show transfinite induction for such large ordinals.
For example, the usual first-order
Peano axioms
do not prove transfinite induction for (or beyond) ε0: while the ordinal ε0 can easily be arithmetically described (it is countable), the Peano axioms are not strong enough to show that it is indeed an ordinal; in fact, transfinite induction on ε0 proves the consistency of Peano's axioms (a theorem by Gentzen
), so by Gödel's second incompleteness theorem, Peano's axioms cannot formalize that reasoning. (This is at the basis of the Kirby–Paris theorem on Goodstein sequences
.) We say that ε0 measures the proof-theoretic strength of Peano's axioms.
But we can do this for systems far beyond Peano's axioms. For example, the proof-theoretic strength of Kripke–Platek set theory
is the Bachmann-Howard ordinal (see below), and, in fact, merely adding to Peano's axioms the axioms that state the well-ordering of all ordinals below the Bachmann–Howard ordinal
is sufficient to obtain all arithmetical consequences of Kripke–Platek set theory
.
, which is the smallest satisfying the equation
, so it is the limit of the sequence 0, 1, 
, 
, 
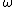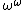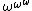, etc. The next ordinal satisfying this equation is called ε1: it is the limit of the sequence
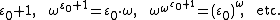
More generally, the
-th ordinal such that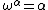 
is called 
. We could define 
as the smallest ordinal such that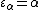 
, but since the Greek alphabet does not have transfinitely many letters it is better to use a more robust notation: define ordinals 
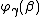by transfinite induction as follows: let 
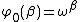and let 
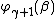be the 
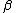-th fixed point of 
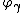(i.e., the 
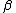-th ordinal such that 
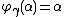; so for example, 
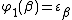), and when 
is a limit ordinal, define 
as the 
-th common fixed point of the 
for all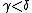 
. This family of functions is known as the Veblen hierarchy. (There are inessential variations in the definition, such as letting, for 
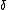a limit ordinal, 
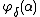be the limit of the 
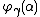for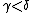 
: this essentially just shifts the indices by 1, which is harmless.) 
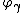is called the 
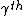Veblen function
(to the base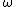
).
Ordering:
if and only if either (
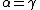and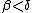 
) or (
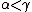and 
) or (
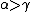and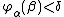 
).
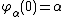is known as the Feferman–Schütte ordinal
and generally written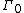
. It can be described as the set of all ordinals that can be written as finite expressions, starting from zero, using only the Veblen hierarchy and addition. The Feferman-Schütte ordinal is important because, in a sense that is complicated to make precise, it is the smallest (infinite) ordinal that cannot be (“predicatively
”) described using smaller ordinals. It measures the strength of such systems as “arithmetical transfinite recursion”.
More generally, Γα enumerates the ordinals that cannot be obtained from smaller ordinals using addition and the Veblen functions.
It is, of course, possible to describe ordinals beyond the Feferman-Schütte ordinal. One could continue to seek fixed points in more and more complicated manner: enumerate the fixed points of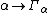
(the first of which is the Ackermann ordinal
), then enumerate the fixed points of that, and so on, and then look for the first ordinal α such that α is obtained in α steps of this process, and continue diagonalizing in this ad hoc manner. This leads to the definition of the “small” and “large” Veblen ordinal
s.
:
Here Ω = ω1 is the first uncountable ordinal. It is put in because otherwise the function ψ gets "stuck" at the smallest ordinal σ such that εσ=σ: in particular ψ(α)=σ for any ordinal α satisfying σ≤α≤Ω. However the fact that we included Ω allows us to get past this point: ψ(Ω+1) is greater than σ. The key property of Ω that we used is that it is greater than any ordinal produced by ψ. This definition is impredicative, because it uses the uncountable ordinal Ω, which, in some sense, already uses all the countable ordinals we are trying to construct in its construction. Likewise, the least-fixed-point operator used in the Veblen hierarchy is not predicative.
To construct still larger ordinals, we can extend the definition of ψ by throwing in more ways of constructing uncountable ordinals. There are several ways to do this, described to some extent in the article on ordinal collapsing function
.
The Bachmann-Howard ordinal (sometimes just called the Howard ordinal, ψ(εΩ+1) with the notation above) is an important one, because it describes the proof-theoretic strength of Kripke-Platek set theory. Indeed, the main importance of these large ordinals, and the reason to describe them, is their relation to certain formal systems as explained above. However, such powerful formal systems as full second-order arithmetic
, let alone Zermelo-Fraenkel set theory, seem beyond reach for the moment.
, Zermelo set theory
, Zermelo-Fraenkel set theory, or Zermelo-Fraenkel set theory with various large cardinal axioms, one gets some extremely large recursive ordinals. (Strictly speaking it is not known that all of these really are ordinals: by construction, the ordinal strength of a theory can only be proven to be an ordinal from an even stronger theory. So for the large cardinal axioms this becomes quite unclear.)
s is an ordinal that is the smallest ordinal that cannot be described in a recursive way. (It is not the order type of any recursive well-ordering of the integers.) That ordinal is a countable ordinal called the Church–Kleene ordinal,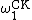
. Thus, 
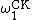is the smallest non-recursive ordinal, and there is no hope of precisely “describing” any ordinals from this point on — we can only define them. But it is still far less than the first uncountable ordinal, 
. However, as its symbol suggests, it behaves in many ways rather like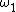 
.
, L, up to stage α, yields a model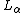
of KP. Such ordinals are called admissible, thus 
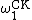is the smallest admissible ordinal (beyond ω in case the axiom of infinity is not included in KP).
By a theorem of Sacks
, the countable admissible ordinals are exactly those constructed in a manner similar to the Church-Kleene ordinal but for Turing machines with oracles
. One sometimes writes
for the 
-th ordinal that is either admissible or a limit of admissible.
is the 
-th admissible ordinal, is called recursively inaccessible. There exists a theory of large ordinals in this manner that is highly parallel to that of (small) large cardinals
. For example, we can define recursively Mahlo ordinals: these are the
such that every 
-recursive closed unbounded subset of 
contains an admissible ordinal (a recursive analog of the definition of a Mahlo cardinal
). But note that we are still talking about possibly countable ordinals here! (While the existence of inaccessible or Mahlo cardinals cannot be proved in Zermelo-Fraenkel set theory, that of recursively inaccessible or recursively Mahlo ordinals is a theorem of ZFC: in fact, any regular cardinal
is recursively Mahlo and more, but even if we limit ourselves to countable ordinals, ZFC proves the existence of recursively Mahlo ordinals. They are, however, beyond the reach of Kripke-Platek set theory.)
An admissible ordinal
is called nonprojectible if there is no total 
-recursive injective function mapping 
into a smaller ordinal. (This is trivially true for regular cardinals; however, we are mainly interested in countable ordinals.) Being nonprojectible is a much stronger condition than being admissible, recursively inaccessible, or even recursively Mahlo. It is equivalent to the statement that the Gödel universe
, L, up to stage α, yields a model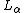
of KP + 
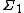-separation.
such that 
is a model of ZFC. Such ordinals are beyond the strength of ZFC in the sense that it cannot (by construction) prove their existence.
Even larger countable ordinals, called the stable ordinals, can be defined by indescribability conditions or as those
such that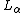 
is a 1-elementary submodel
of L; the existence of these ordinals can be proven in ZFC, and they are closely related to the nonprojectible ordinals.
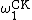. Every recursively enumerable (or even hyperarithmetic) nonempty subset of this total ordering has a least element. So it resembles a well-ordering in some respects. For example, one can define the arithmetic operations on it. Yet it is not possible to effectively determine exactly where the initial well-ordered part ends and the part lacking a least element begins.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, there are many ways of describing specific countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
ordinals
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
. The smallest ones can be usefully and non-circularly expressed in terms of their Cantor normal forms. Beyond that, many ordinals of relevance to proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
still have computable
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
ordinal notation
Ordinal notation
In mathematical logic and set theory, an ordinal notation is a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language....
s. However, it is not possible to decide effectively whether a given putative ordinal notation is a notation or not (for reasons somewhat analogous to the unsolvability of the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
); various more-concrete ways of defining ordinals that definitely have notations are available.
Since there are only countably many notations, all ordinals with notations are exhausted well below the first uncountable ordinal ω1
First uncountable ordinal
In mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
; their supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
is called Church–Kleene ω1 or ω1CK (not to be confused with the first uncountable ordinal, ω1), described below. Ordinal numbers below ω1CK are the recursive ordinals (see below). Countable ordinals larger than this may still be defined, but do not have notations.
Due to the focus on countable ordinals, ordinal arithmetic
Ordinal arithmetic
In the mathematical field of set theory, ordinal arithmetic describes the three usual operations on ordinal numbers: addition, multiplication, and exponentiation. Each can be defined in essentially two different ways: either by constructing an explicit well-ordered set which represents the...
is used throughout, except where otherwise noted. The ordinals described here are not as large as the ones described in large cardinals, but they are large among those that have constructive notations (descriptions). Larger and larger ordinals can be defined, but they become more and more difficult to describe.
Ordinal notations
Recursive ordinalRecursive ordinal
In mathematics, specifically set theory, an ordinal \alpha is said to be recursive if there is a recursive binary relation R that well-orders a subset of the natural numbers and the order type of that ordering is \alpha....
s (or computable ordinals) are certain countable ordinals: loosely speaking those represented by a computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
. There are several equivalent definitions of this: the simplest is to say that a computable ordinal is the order-type of some recursive (i.e., computable) well-ordering of the natural numbers; so, essentially, an ordinal is recursive when we can present the set of smaller ordinals in such a way that a computer (Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
, say) can manipulate them (and, essentially, compare them).
A different definition uses Kleene
Stephen Cole Kleene
Stephen Cole Kleene was an American mathematician who helped lay the foundations for theoretical computer science...
's system of ordinal notation
Ordinal notation
In mathematical logic and set theory, an ordinal notation is a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language....
s. Briefly, an ordinal notation is either the name zero (describing the ordinal 0), or the successor of an ordinal notation (describing the successor of the ordinal described by that notation), or a Turing machine (computable function) that produces an increasing sequence of ordinal notations (that describe the ordinal that is the limit of the sequence), and ordinal notations are (partially) ordered so as to make the successor of o greater than o and to make the limit greater than any term of the sequence (this order is computable; however, the set O of ordinal notations itself is highly non-recursive, owing to the impossibility of deciding whether a given Turing machine does indeed produce a sequence of notations); a recursive ordinal is then an ordinal described by some ordinal notation.
Any ordinal smaller than a recursive ordinal is itself recursive, so the set of all recursive ordinals forms a certain (countable) ordinal, the Church-Kleene ordinal (see below).
It is tempting to forget about ordinal notations, and only speak of the recursive ordinals themselves: and some statements are made about recursive ordinals which, in fact, concern the notations for these ordinals. This leads to difficulties, however, as even the smallest infinite ordinal, ω, has many notations, some of which cannot be proven to be equivalent to the obvious notation (the limit of the simplest program that enumerates all natural numbers).
Relationship to systems of arithmetic
There is a relation between computable ordinals and certain formal systemFormal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
s (containing arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
, that is, at least a reasonable fragment of Peano arithmetic
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
).
Certain computable ordinals are so large that while they can be given by a certain ordinal notation o, a given formal system might not be sufficiently powerful to show that o is, indeed, an ordinal notation: the system does not show transfinite induction for such large ordinals.
For example, the usual first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
Peano axioms
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
do not prove transfinite induction for (or beyond) ε0: while the ordinal ε0 can easily be arithmetically described (it is countable), the Peano axioms are not strong enough to show that it is indeed an ordinal; in fact, transfinite induction on ε0 proves the consistency of Peano's axioms (a theorem by Gentzen
Gerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
), so by Gödel's second incompleteness theorem, Peano's axioms cannot formalize that reasoning. (This is at the basis of the Kirby–Paris theorem on Goodstein sequences
Goodstein's theorem
In mathematical logic, Goodstein's theorem is a statement about the natural numbers, made by Reuben Goodstein, which states that every Goodstein sequence eventually terminates at 0. showed that it is unprovable in Peano arithmetic...
.) We say that ε0 measures the proof-theoretic strength of Peano's axioms.
But we can do this for systems far beyond Peano's axioms. For example, the proof-theoretic strength of Kripke–Platek set theory
Kripke–Platek set theory
The Kripke–Platek axioms of set theory are a system of axioms for axiomatic set theory developed by Saul Kripke and Richard Platek. The axiom system, written in first-order logic, has an infinite number of axioms because an infinite axiom schema is used.KP is weaker than Zermelo–Fraenkel set theory...
is the Bachmann-Howard ordinal (see below), and, in fact, merely adding to Peano's axioms the axioms that state the well-ordering of all ordinals below the Bachmann–Howard ordinal
Bachmann–Howard ordinal
In mathematics, the Bachmann–Howard ordinal is a large countable ordinal.It is the proof theoretic ordinal of several mathematical theories, such as Kripke–Platek set theory and the system CZF of constructive set theory.It is named after William Alvin Howard and Heinz Bachmann.-Definition:The...
is sufficient to obtain all arithmetical consequences of Kripke–Platek set theory
Kripke–Platek set theory
The Kripke–Platek axioms of set theory are a system of axioms for axiomatic set theory developed by Saul Kripke and Richard Platek. The axiom system, written in first-order logic, has an infinite number of axioms because an infinite axiom schema is used.KP is weaker than Zermelo–Fraenkel set theory...
.
Predicative definitions and the Veblen hierarchy
We have already mentioned (see Cantor normal form) the ordinal ε0Epsilon nought
In mathematics, the epsilon numbers are a collection of transfinite numbers whose defining property is that they are fixed points of an exponential map. Consequently, they are not reachable from 0 via a finite series of applications of the chosen exponential map and of "weaker" operations like...
, which is the smallest satisfying the equation
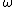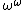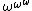, so it is the limit of the sequence 0, 1, , , , etc. The next ordinal satisfying this equation is called ε1: it is the limit of the sequence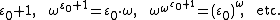More generally, the
-th ordinal such that 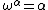is called . We could define as the smallest ordinal such that 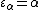, but since the Greek alphabet does not have transfinitely many letters it is better to use a more robust notation: define ordinals 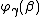by transfinite induction as follows: let 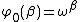and let 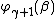be the 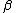-th fixed point of 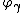(i.e., the 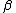-th ordinal such that 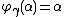; so for example, 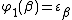), and when is a limit ordinal, define as the -th common fixed point of the for all 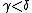. This family of functions is known as the Veblen hierarchy. (There are inessential variations in the definition, such as letting, for 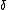a limit ordinal, 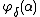be the limit of the 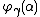for 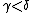: this essentially just shifts the indices by 1, which is harmless.) 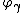is called the 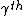Veblen functionVeblen function
In mathematics, the Veblen functions are a hierarchy of normal functions , introduced by Oswald Veblen in...
(to the base
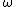).Ordering:
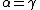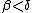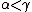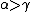if and only if either ( and ) or ( and ) or ( and 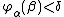).The Feferman–Schütte ordinal and beyond
The smallest ordinal such that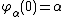 is known as the Feferman–Schütte ordinalFeferman–Schütte ordinal
In mathematics, the Feferman–Schütte ordinal Γ0 is a large countable ordinal.It is the proof theoretic ordinal of several mathematical theories, such as arithmetical transfinite recursion.It is named after Solomon Feferman and Kurt Schütte....
and generally written
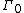. It can be described as the set of all ordinals that can be written as finite expressions, starting from zero, using only the Veblen hierarchy and addition. The Feferman-Schütte ordinal is important because, in a sense that is complicated to make precise, it is the smallest (infinite) ordinal that cannot be (“predicativelyImpredicative
In mathematics and logic, impredicativity is the property of a self-referencing definition. More precisely, a definition is said to be impredicative if it invokes the set being defined, or another set which contains the thing being defined.Russell's paradox is a famous example of an impredicative...
”) described using smaller ordinals. It measures the strength of such systems as “arithmetical transfinite recursion”.
More generally, Γα enumerates the ordinals that cannot be obtained from smaller ordinals using addition and the Veblen functions.
It is, of course, possible to describe ordinals beyond the Feferman-Schütte ordinal. One could continue to seek fixed points in more and more complicated manner: enumerate the fixed points of
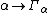(the first of which is the Ackermann ordinalAckermann ordinal
In mathematics, the Ackermann ordinal is a certain large countable ordinal, named after Wilhelm Ackermann. The term "Ackermann ordinal" is also occasionally used for the small Veblen ordinal, a somewhat larger ordinal....
), then enumerate the fixed points of that, and so on, and then look for the first ordinal α such that α is obtained in α steps of this process, and continue diagonalizing in this ad hoc manner. This leads to the definition of the “small” and “large” Veblen ordinal
Veblen ordinal
In mathematics, the Veblen ordinal is either of two large countable ordinals:*The small Veblen ordinal*The large Veblen ordinal...
s.
Impredicative ordinals
To go far beyond the Feferman-Schütte ordinal, one needs to introduce new methods. Unfortunately there is not yet any standard way to do this: every author in the subject seems to have invented their own system of notation, and it is quite hard to translate between the different systems. The first such system was introduced by Bachmann in 1950 (in an ad hoc manner), and different extensions and variations of it were described by Buchholz, Takeuti (ordinal diagrams), Feferman (θ systems), Aczel, Bridge, Schütte, and Pohlers. However most systems use the same basic idea, of constructing new countable ordinals by using the existence of certain uncountable ordinals. Here is an example of such a definition, described in much greater detail in the article on ordinal collapsing functionOrdinal collapsing function
In mathematical logic and set theory, an ordinal collapsing function is a technique for defining certain recursive large countable ordinals, whose principle is to give names to certain ordinals much larger than the one being defined, perhaps even large cardinals In mathematical logic and set...
:
- ψ(α) is defined to be the smallest ordinal that cannot be constructed by starting with 0, 1, ω and Ω, and repeatedly applying addition, multiplication and exponentiation, and ψ to previously constructed ordinals (except that ψ can only be applied to arguments less than α, to ensure that it is well defined).
Here Ω = ω1 is the first uncountable ordinal. It is put in because otherwise the function ψ gets "stuck" at the smallest ordinal σ such that εσ=σ: in particular ψ(α)=σ for any ordinal α satisfying σ≤α≤Ω. However the fact that we included Ω allows us to get past this point: ψ(Ω+1) is greater than σ. The key property of Ω that we used is that it is greater than any ordinal produced by ψ. This definition is impredicative, because it uses the uncountable ordinal Ω, which, in some sense, already uses all the countable ordinals we are trying to construct in its construction. Likewise, the least-fixed-point operator used in the Veblen hierarchy is not predicative.
To construct still larger ordinals, we can extend the definition of ψ by throwing in more ways of constructing uncountable ordinals. There are several ways to do this, described to some extent in the article on ordinal collapsing function
Ordinal collapsing function
In mathematical logic and set theory, an ordinal collapsing function is a technique for defining certain recursive large countable ordinals, whose principle is to give names to certain ordinals much larger than the one being defined, perhaps even large cardinals In mathematical logic and set...
.
The Bachmann-Howard ordinal (sometimes just called the Howard ordinal, ψ(εΩ+1) with the notation above) is an important one, because it describes the proof-theoretic strength of Kripke-Platek set theory. Indeed, the main importance of these large ordinals, and the reason to describe them, is their relation to certain formal systems as explained above. However, such powerful formal systems as full second-order arithmetic
Second-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
, let alone Zermelo-Fraenkel set theory, seem beyond reach for the moment.
“Unrecursable” recursive ordinals
By dropping the requirement of having a useful description, even larger recursive countable ordinals can be obtained as the ordinals measuring the strengths of various strong theories; roughly speaking, these ordinals are the smallest ordinals that the theories cannot prove are well ordered. By taking stronger and stronger theories such as second-order arithmeticSecond-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
, Zermelo set theory
Zermelo set theory
Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
, Zermelo-Fraenkel set theory, or Zermelo-Fraenkel set theory with various large cardinal axioms, one gets some extremely large recursive ordinals. (Strictly speaking it is not known that all of these really are ordinals: by construction, the ordinal strength of a theory can only be proven to be an ordinal from an even stronger theory. So for the large cardinal axioms this becomes quite unclear.)
The Church–Kleene ordinal
The set of recursive ordinalRecursive ordinal
In mathematics, specifically set theory, an ordinal \alpha is said to be recursive if there is a recursive binary relation R that well-orders a subset of the natural numbers and the order type of that ordering is \alpha....
s is an ordinal that is the smallest ordinal that cannot be described in a recursive way. (It is not the order type of any recursive well-ordering of the integers.) That ordinal is a countable ordinal called the Church–Kleene ordinal,
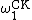. Thus, 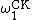is the smallest non-recursive ordinal, and there is no hope of precisely “describing” any ordinals from this point on — we can only define them. But it is still far less than the first uncountable ordinal, . However, as its symbol suggests, it behaves in many ways rather like 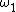.Admissible ordinals
The Church-Kleene ordinal is again related to Kripke-Platek set theory, but now in a different way: whereas the Bachmann-Howard ordinal (described above) was the smallest ordinal for which KP does not prove transfinite induction, the Church-Kleene ordinal is the smallest α such that the construction of the Gödel universeConstructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
, L, up to stage α, yields a model
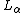of KP. Such ordinals are called admissible, thus 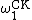is the smallest admissible ordinal (beyond ω in case the axiom of infinity is not included in KP).By a theorem of Sacks
Gerald Sacks
Gerald Sacks is a logician who holds a joint appointment at Harvard University as a Professor of Mathematical Logic and the Massachusetts Institute of Technology as a Professor Emeritus. His most important contributions have been in recursion theory...
, the countable admissible ordinals are exactly those constructed in a manner similar to the Church-Kleene ordinal but for Turing machines with oracles
Oracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
. One sometimes writes
for the -th ordinal that is either admissible or a limit of admissible.Beyond admissible ordinals
An ordinal that is both admissible and a limit of admissibles, or equivalently such that is the -th admissible ordinal, is called recursively inaccessible. There exists a theory of large ordinals in this manner that is highly parallel to that of (small) large cardinalsLarge cardinal property
In the mathematical field of set theory, a large cardinal property is a certain kind of property of transfinite cardinal numbers. Cardinals with such properties are, as the name suggests, generally very "large"...
. For example, we can define recursively Mahlo ordinals: these are the
such that every -recursive closed unbounded subset of contains an admissible ordinal (a recursive analog of the definition of a Mahlo cardinalMahlo cardinal
In mathematics, a Mahlo cardinal is a certain kind of large cardinal number. Mahlo cardinals were first described by . As with all large cardinals, none of these varieties of Mahlo cardinals can be proved to exist by ZFC ....
). But note that we are still talking about possibly countable ordinals here! (While the existence of inaccessible or Mahlo cardinals cannot be proved in Zermelo-Fraenkel set theory, that of recursively inaccessible or recursively Mahlo ordinals is a theorem of ZFC: in fact, any regular cardinal
Regular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
is recursively Mahlo and more, but even if we limit ourselves to countable ordinals, ZFC proves the existence of recursively Mahlo ordinals. They are, however, beyond the reach of Kripke-Platek set theory.)
An admissible ordinal
is called nonprojectible if there is no total -recursive injective function mapping into a smaller ordinal. (This is trivially true for regular cardinals; however, we are mainly interested in countable ordinals.) Being nonprojectible is a much stronger condition than being admissible, recursively inaccessible, or even recursively Mahlo. It is equivalent to the statement that the Gödel universeConstructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
, L, up to stage α, yields a model
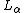of KP + 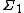-separation.“Unprovable” ordinals
We can imagine even larger ordinals that are still countable. For example, if ZFC has a transitive model (a hypothesis stronger than the mere hypothesis of consistency, and implied by the existence of an inaccessible cardinal), then there exists a countable such that is a model of ZFC. Such ordinals are beyond the strength of ZFC in the sense that it cannot (by construction) prove their existence.Even larger countable ordinals, called the stable ordinals, can be defined by indescribability conditions or as those
such that 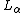is a 1-elementary submodelElementary equivalence
In model theory, a field within mathematical logic, two structures M and N of the same signature σ are called elementarily equivalent if they satisfy the same first-order σ-sentences....
of L; the existence of these ordinals can be proven in ZFC, and they are closely related to the nonprojectible ordinals.
A pseudo-well-ordering
Within the scheme of notations of Kleene some represent ordinals and some do not. One can define a recursive total ordering that is a subset of the Kleene notations and has an initial segment which is well-ordered with order-type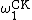. Every recursively enumerable (or even hyperarithmetic) nonempty subset of this total ordering has a least element. So it resembles a well-ordering in some respects. For example, one can define the arithmetic operations on it. Yet it is not possible to effectively determine exactly where the initial well-ordered part ends and the part lacking a least element begins.On recursive ordinals
- Wolfram Pohlers, Proof theory, Springer 1989 ISBN 0-387-51842-8 (for Veblen hierarchy and some impredicative ordinals). This is probably the most readable book on large countable ordinals (which is not saying much).
- Gaisi TakeutiGaisi Takeutiis a Japanese mathematician, known for his work in proof theory.After graduating from Tokyo University, he went to Princeton to study under Kurt Gödel.He later became a professor at the University of Illinois at Urbana-Champaign...
, Proof theory, 2nd edition 1987 ISBN 0-444-10492-5 (for ordinal diagrams) - Kurt SchütteKurt SchütteKurt Schütte was a German mathematician who worked on proof theory and ordinal analysis. The Feferman-Schütte ordinal, which he showed to be the precise ordinal bound for predicativity, is named after him.-References:...
, Proof theory, Springer 1977 ISBN 0-387-07911-4 (for Veblen hierarchy and some impredicative ordinals) - Craig Smorynski, The varieties of arboreal experience Math. Intelligencer 4 (1982), no. 4, 182–189; contains an informal description of the Veblen hierarchy.
- Hartley Rogers, Jr., Theory of Recursive Functions and Effective Computability McGraw-Hill (1967) ISBN 0-262-68052-1 (describes recursive ordinals and the Church–Kleene ordinal)
- Larry W. Miller, Normal Functions and Constructive Ordinal Notations, The Journal of Symbolic Logic, volume 41, number 2, June 1976, pages 439 to 459, ,
- Hilbert Levitz, Transfinite Ordinals and Their Notations: For The Uninitiated, expository article (8 pages, in PostScriptPostScriptPostScript is a dynamically typed concatenative programming language created by John Warnock and Charles Geschke in 1982. It is best known for its use as a page description language in the electronic and desktop publishing areas. Adobe PostScript 3 is also the worldwide printing and imaging...
) - Herman Ruge Jervell, Truth and provability, manuscript in progress.
Both recursive and nonrecursive ordinals
- Michael Rathjen, "The realm of ordinal analysis." in S. Cooper and J. Truss (eds.): Sets and Proofs. (Cambridge University Press, 1999) 219–279. At Postscript file.