Elementary equivalence
Encyclopedia
In model theory
, a field within mathematical logic
, two structure
s M and N of the same signature σ are called elementarily equivalent if they satisfy the same first-order
σ-sentences.
If N is a substructure
of M, one often needs a stronger condition. In this case N is called an elementary substructure of M if every first-order σ-formula φ(a1, …, an) with parameters a1, …, an from N is true in N if and only if it is true in M.
If N is an elementary substructure of M, M is called an elementary extension of N. An embedding h: N → M is called an elementary embedding of N into M if h(N) is an elementary substructure of M.
A substructure
N of M is elementary if and only if it passes the Tarski–Vaught test: Every first-order formula φ(x, b1, …, bn) with parameters in N that has a solution in M also has a solution in N when evaluated in M. One can prove that two structures are elementary equivalent with the Ehrenfeucht–Fraïssé games.
.
If M and N are elementarily equivalent, one writes M ≡ N.
A first-order theory
is complete if and only if any two of its models are elementarily equivalent.
For example, consider the language with one binary relation symbol '<'. The model R of real numbers with its usual order and the model Q of rational numbers with its usual order are elementarily equivalent, since they both interpret '<' as an unbounded dense linear ordering. This is sufficient to ensure elementary equivalence, because the theory of unbounded dense linear orderings is complete, as can be shown by Vaught's test.
More generally, any first-order theory has non-isomorphic, elementary equivalent models, which can be obtained via the Löwenheim–Skolem theorem
. Thus, for example, there are non-standard model
s of Peano arithmetic, which contain other objects than just the numbers 0, 1, 2, etc., and yet are elementarily equivalent to the standard model.
It follows that N is a substructure of M.
If N is a substructure of M, then both N and M can be interpreted as structures in the signature σN consisting of σ together with a new constant symbol for every element of N. N is an elementary substructure of M if and only if N is a substructure of M and N and M are elementarily equivalent as σN-structures.
If N is an elementary substructure of M, one writes N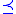
M and says that M is an elementary extension of N: M 
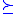N.
The downward Löwenheim–Skolem theorem
gives a countable elementary substructure for any infinite first-order structure; the upward Löwenheim–Skolem theorem gives elementary extensions of any infinite first-order structure of arbitrarily large cardinality.
Let M be a structure of signature σ and N a substructure of M. N is an elementary substructure of M if and only if for every first-order formula φ(x, y1, …, yn) over σ and all elements b1, …, bn from N, if M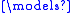
x φ(x, b1, …, bn), then there is an element a in N such that M 
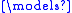φ(a, b1, …, bn).
Every elementary embedding is a strong homomorphism, and its image is an elementary substructure.
Elementary embeddings are the most important maps in model theory. In set theory
, elementary embeddings whose domain is V (the universe of set theory) play an important role in the theory of large cardinals (see also critical point
).
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, a field within mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, two structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
s M and N of the same signature σ are called elementarily equivalent if they satisfy the same first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
σ-sentences.
If N is a substructure
Substructure
In mathematical logic, an substructure or subalgebra is a structure whose domain is a subset of that of a bigger structure, and whose functions and relations are the traces of the functions and relations of the bigger structure...
of M, one often needs a stronger condition. In this case N is called an elementary substructure of M if every first-order σ-formula φ(a1, …, an) with parameters a1, …, an from N is true in N if and only if it is true in M.
If N is an elementary substructure of M, M is called an elementary extension of N. An embedding h: N → M is called an elementary embedding of N into M if h(N) is an elementary substructure of M.
A substructure
Substructure
In mathematical logic, an substructure or subalgebra is a structure whose domain is a subset of that of a bigger structure, and whose functions and relations are the traces of the functions and relations of the bigger structure...
N of M is elementary if and only if it passes the Tarski–Vaught test: Every first-order formula φ(x, b1, …, bn) with parameters in N that has a solution in M also has a solution in N when evaluated in M. One can prove that two structures are elementary equivalent with the Ehrenfeucht–Fraïssé games.
Elementarily equivalent structures
Two structures M and N of the same signature σ are elementarily equivalent if every first-order sentence (formula without free variables) over σ is true in M if and only if it is true in N, i.e. if M and N have the same complete first-order theoryComplete theory
In mathematical logic, a theory is complete if it is a maximal consistent set of sentences, i.e., if it is consistent, and none of its proper extensions is consistent...
.
If M and N are elementarily equivalent, one writes M ≡ N.
A first-order theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
is complete if and only if any two of its models are elementarily equivalent.
For example, consider the language with one binary relation symbol '<'. The model R of real numbers with its usual order and the model Q of rational numbers with its usual order are elementarily equivalent, since they both interpret '<' as an unbounded dense linear ordering. This is sufficient to ensure elementary equivalence, because the theory of unbounded dense linear orderings is complete, as can be shown by Vaught's test.
More generally, any first-order theory has non-isomorphic, elementary equivalent models, which can be obtained via the Löwenheim–Skolem theorem
Löwenheim–Skolem theorem
In mathematical logic, the Löwenheim–Skolem theorem, named for Leopold Löwenheim and Thoralf Skolem, states that if a countable first-order theory has an infinite model, then for every infinite cardinal number κ it has a model of size κ...
. Thus, for example, there are non-standard model
Non-standard model
In model theory, a discipline within mathematical logic, a non-standard model is a model of a theory that is not isomorphic to the intended model . If the intended model is infinite and the language is first-order, then the Löwenheim-Skolem theorems guarantee the existence of non-standard models...
s of Peano arithmetic, which contain other objects than just the numbers 0, 1, 2, etc., and yet are elementarily equivalent to the standard model.
Elementary substructures and elementary extensions
N is an elementary substructure of M if N and M are structures of the same signature σ such that for all first-order σ-formulas φ(x1, …, xn) with free variables x1, …, xn, and all elements a1, …, an of N, φ(a1, …, an) holds in N if and only if it holds in M:- N
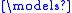φ(a1, …, an) iff M 
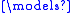φ(a1, …, an).
It follows that N is a substructure of M.
If N is a substructure of M, then both N and M can be interpreted as structures in the signature σN consisting of σ together with a new constant symbol for every element of N. N is an elementary substructure of M if and only if N is a substructure of M and N and M are elementarily equivalent as σN-structures.
If N is an elementary substructure of M, one writes N
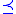M and says that M is an elementary extension of N: M 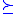N.The downward Löwenheim–Skolem theorem
Löwenheim–Skolem theorem
In mathematical logic, the Löwenheim–Skolem theorem, named for Leopold Löwenheim and Thoralf Skolem, states that if a countable first-order theory has an infinite model, then for every infinite cardinal number κ it has a model of size κ...
gives a countable elementary substructure for any infinite first-order structure; the upward Löwenheim–Skolem theorem gives elementary extensions of any infinite first-order structure of arbitrarily large cardinality.
Tarski–Vaught test
The Tarski–Vaught test (or Tarski–Vaught criterion) is a necessary and sufficient condition for a substructure N of a structure M to be an elementary substructure. It can be useful for constructing an elementary substructure of a large structure.Let M be a structure of signature σ and N a substructure of M. N is an elementary substructure of M if and only if for every first-order formula φ(x, y1, …, yn) over σ and all elements b1, …, bn from N, if M
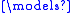x φ(x, b1, …, bn), then there is an element a in N such that M 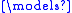φ(a, b1, …, bn).Elementary embeddings
An elementary embedding of a structure N into a structure M of the same signature σ is a map h: N → M such that for every first-order σ-formula φ(x1, …, xn) and all elements a1, …, an of N,- N
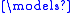φ(a1, …, an) implies M 
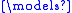φ(h(a1), …, h(an)).
Every elementary embedding is a strong homomorphism, and its image is an elementary substructure.
Elementary embeddings are the most important maps in model theory. In set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, elementary embeddings whose domain is V (the universe of set theory) play an important role in the theory of large cardinals (see also critical point
Critical point (set theory)
In set theory, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal which is not mapped to itself....
).