Recursive ordinal
Encyclopedia
In mathematics
, specifically set theory
, an ordinal
is said to be recursive if there is a recursive
binary relation
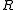that well-order
s a subset
of the natural numbers and the order type
of that ordering is
.
It is trivial to check that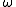
is recursive, the successor
of a recursive ordinal is recursive, and the set of all recursive ordinals is closed
downwards. We call the supremum
of all recursive ordinals the Church-Kleene ordinal and denote it by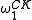
. Since the recursive relations are parameterized
by the natural numbers, the recursive ordinals are also parameterized by the natural numbers. Therefore, there are only countably many recursive ordinals. Thus,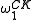
is countable.
The recursive ordinals are exactly the ordinals that have an ordinal notation
in Kleene's
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, an ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
is said to be recursive if there is a recursiveRecursive set
In computability theory, a set of natural numbers is called recursive, computable or decidable if there is an algorithm which terminates after a finite amount of time and correctly decides whether or not a given number belongs to the set....
binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
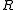that well-orderWell-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
s a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the natural numbers and the order type
Order type
In mathematics, especially in set theory, two ordered sets X,Y are said to have the same order type just when they are order isomorphic, that is, when there exists a bijection f: X → Y such that both f and its inverse are monotone...
of that ordering is
.It is trivial to check that
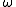is recursive, the successorSuccessor ordinal
In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
of a recursive ordinal is recursive, and the set of all recursive ordinals is closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
downwards. We call the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of all recursive ordinals the Church-Kleene ordinal and denote it by
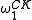. Since the recursive relations are parameterizedParameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
by the natural numbers, the recursive ordinals are also parameterized by the natural numbers. Therefore, there are only countably many recursive ordinals. Thus,
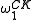is countable.The recursive ordinals are exactly the ordinals that have an ordinal notation
Ordinal notation
In mathematical logic and set theory, an ordinal notation is a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language....
in Kleene's
.