
Bachmann–Howard ordinal
Encyclopedia
In mathematics, the Bachmann–Howard ordinal (or Howard ordinal) is a large countable ordinal
.
It is the proof theoretic ordinal
of several mathematical theories, such as Kripke–Platek set theory
(with the axiom of infinity
) and the system CZF of constructive set theory
.
It is named after William Alvin Howard
and Heinz Bachmann.
(with more details given in the relevant article):
The Bachmann–Howard ordinal can also be defined as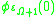 for an extension of the Veblen function
for an extension of the Veblen function
s φα to uncountable α; this extension is not completely straightforward.
Large countable ordinal
In the mathematical discipline of set theory, there are many ways of describing specific countable ordinals. The smallest ones can be usefully and non-circularly expressed in terms of their Cantor normal forms. Beyond that, many ordinals of relevance to proof theory still have computable ordinal...
.
It is the proof theoretic ordinal
Ordinal analysis
In proof theory, ordinal analysis assigns ordinals to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε0.-Definition:Ordinal...
of several mathematical theories, such as Kripke–Platek set theory
Kripke–Platek set theory
The Kripke–Platek axioms of set theory are a system of axioms for axiomatic set theory developed by Saul Kripke and Richard Platek. The axiom system, written in first-order logic, has an infinite number of axioms because an infinite axiom schema is used.KP is weaker than Zermelo–Fraenkel set theory...
(with the axiom of infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
) and the system CZF of constructive set theory
Constructive set theory
Constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. That is, it uses the usual first-order language of classical set theory, and although of course the logic is constructive, there is no explicit use of constructive types...
.
It is named after William Alvin Howard
William Alvin Howard
William Alvin Howard is a proof theorist best known for his work demonstrating formal similarity between intuitionistic logic and the simply typed lambda calculus that has come to be known as the Curry–Howard correspondence. He has also been active in the theory of proof-theoretic ordinals. He...
and Heinz Bachmann.
Definition
The Bachmann–Howard ordinal is defined using an ordinal collapsing functionOrdinal collapsing function
In mathematical logic and set theory, an ordinal collapsing function is a technique for defining certain recursive large countable ordinals, whose principle is to give names to certain ordinals much larger than the one being defined, perhaps even large cardinals In mathematical logic and set...
(with more details given in the relevant article):
- εα enumerates the epsilon numbersEpsilon noughtIn mathematics, the epsilon numbers are a collection of transfinite numbers whose defining property is that they are fixed points of an exponential map. Consequently, they are not reachable from 0 via a finite series of applications of the chosen exponential map and of "weaker" operations like...
, the ordinals ε such that ωε = ε. - Ω = ω1 is the first uncountable ordinalFirst uncountable ordinalIn mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
. - εΩ+1 is the first epsilon number after Ω = εΩ.
- ψ(0) is defined to be the smallest ordinal that cannot be constructed by starting with 0, 1, ω and Ω, and repeatedly applying ordinal addition, multiplication and exponentiation.
- ψ(α) is defined in the same way, except that it also allows applications of ψ to previously constructed ordinals less than α.
- The Bachmann–Howard ordinal is ψ(εΩ+1).
The Bachmann–Howard ordinal can also be defined as
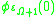 for an extension of the Veblen function
for an extension of the Veblen functionVeblen function
In mathematics, the Veblen functions are a hierarchy of normal functions , introduced by Oswald Veblen in...
s φα to uncountable α; this extension is not completely straightforward.

