Equation of the center
Encyclopedia
For further closely related mathematical developments see also Two-body problem
, also Gravitational two-body problem
, also Kepler orbit
, and Kepler problem
The equation of the center, in astronomy
and elliptical motion
, is equal to the true anomaly
minus the mean anomaly
, i.e. the difference between the actual angular position in the elliptical orbit and the position the orbiting body would have if its angular motion was uniform. It arises from the ellipticity of the orbit, is zero at pericenter and apocenter, and reaches its greatest amount nearly midway between these points.
The "equation" in the present sense comes from astronomy. It was specified and used by Kepler,
as that variable quantity determined by calculation which must be added or subtracted from the mean motion to obtain the true motion. It is based on aequatio, nis in Latin
. In the expression "equation of time" used in astronomy, the term "equation" has a similar meaning.
, the true anomaly, 
, may be expressed as a sine
series of the mean anomaly,
. The following shows the series expanded to terms of the order of 
:
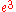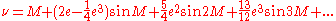
Related expansions may be used to express the true distance
of the orbiting body from the central body as a fraction of the semi-major axis
of the ellipse,
;
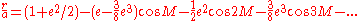or the inverse of this distance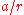
has sometimes been used (e.g. it is proportional to the horizontal parallax of the orbiting body as seen from the central body):
.
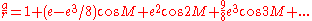Series such as these can be used as part of the preparation of approximate tables of motion of astronomical objects, such as that of the moon
around the earth
, or the earth or other planet
s around the sun
, when perturbations
of the motion are included as well.
, known as the principal term of the equation of the center, has a coefficient of 22639.55", approximately 0.1098 radian
s, or 6.289° (degrees
).
The earliest known estimates of a parameter corresponding to the Moon's equation of the center are Hipparchus
' estimates, based on a theory in which the Moon's orbit followed an epicycle or eccenter carried around a circular deferent. (The parameter in the Hipparchan theory corresponding to the equation of the center was the radius of the epicycle as a proportion of the radius of the main orbital circle.) Hipparchus' estimates, based on his data as corrected by Ptolemy
yield a figure close to 5° (degrees).
Most of the discrepancy between the Hipparchan estimates and the modern value of the equation of the center arises because Hipparchus' data were taken from positions of the Moon at times of eclipses,. He did not recognize the perturbation now called the evection
. At new and full moons the evection opposes the equation of the center, to the extent of the coefficient of the evection, 4586.45". The Hipparchus parameter for the relative size of the Moon's epicycle corresponds quite closely to the difference between the two modern coefficients, of the equation of the center, and of the evection (difference 18053.1", about 5.01°).
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
, also Gravitational two-body problem
Gravitational two-body problem
For further relevant mathematical developments see also Two-body problem, also Kepler orbit, and Kepler problem, and Equation of the center – Analytical expansions...
, also Kepler orbit
Kepler orbit
In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
, and Kepler problem
Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
The equation of the center, in astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
and elliptical motion
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, is equal to the true anomaly
True anomaly
In celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
minus the mean anomaly
Mean anomaly
In celestial mechanics, the mean anomaly is a parameter relating position and time for a body moving in a Kepler orbit. It is based on the fact that equal areas are swept at the focus in equal intervals of time....
, i.e. the difference between the actual angular position in the elliptical orbit and the position the orbiting body would have if its angular motion was uniform. It arises from the ellipticity of the orbit, is zero at pericenter and apocenter, and reaches its greatest amount nearly midway between these points.
The "equation" in the present sense comes from astronomy. It was specified and used by Kepler,
as that variable quantity determined by calculation which must be added or subtracted from the mean motion to obtain the true motion. It is based on aequatio, nis in Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
. In the expression "equation of time" used in astronomy, the term "equation" has a similar meaning.
Analytical expansions
For small values of orbital eccentricity,, the true anomaly, , may be expressed as a sineSine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
series of the mean anomaly,
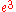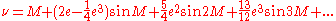
. The following shows the series expanded to terms of the order of :Related expansions may be used to express the true distance
of the orbiting body from the central body as a fraction of the semi-major axisSemi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
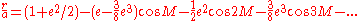of the ellipse, ;or the inverse of this distance
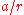has sometimes been used (e.g. it is proportional to the horizontal parallax of the orbiting body as seen from the central body): 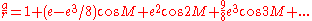.Series such as these can be used as part of the preparation of approximate tables of motion of astronomical objects, such as that of the moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
around the earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
, or the earth or other planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s around the sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
, when perturbations
Perturbation (astronomy)
Perturbation is a term used in astronomy in connection with descriptions of the complex motion of a massive body which is subject to appreciable gravitational effects from more than one other massive body....
of the motion are included as well.
Moon's equation of the center
In the case of the moon, its orbit around the earth has an eccentricity of approximately 0.0549. The term in, known as the principal term of the equation of the center, has a coefficient of 22639.55", approximately 0.1098 radianRadian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s, or 6.289° (degrees
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
).
The earliest known estimates of a parameter corresponding to the Moon's equation of the center are Hipparchus
Hipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
' estimates, based on a theory in which the Moon's orbit followed an epicycle or eccenter carried around a circular deferent. (The parameter in the Hipparchan theory corresponding to the equation of the center was the radius of the epicycle as a proportion of the radius of the main orbital circle.) Hipparchus' estimates, based on his data as corrected by Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
yield a figure close to 5° (degrees).
Most of the discrepancy between the Hipparchan estimates and the modern value of the equation of the center arises because Hipparchus' data were taken from positions of the Moon at times of eclipses,. He did not recognize the perturbation now called the evection
Evection
Evection , in astronomy, is the largest inequality produced by the action of the Sun in the monthly revolution of the Moon around the Earth. The evection, formerly called the moon's second anomaly, was approximately known in ancient times, and its discovery is attributed to Ptolemy...
. At new and full moons the evection opposes the equation of the center, to the extent of the coefficient of the evection, 4586.45". The Hipparchus parameter for the relative size of the Moon's epicycle corresponds quite closely to the difference between the two modern coefficients, of the equation of the center, and of the evection (difference 18053.1", about 5.01°).