
Equidistribution theorem
Encyclopedia
In mathematics
, the equidistribution theorem is the statement that the sequence
is uniformly distributed on the unit interval
, when a is an irrational number
. It is a special case of the ergodic theorem.
, Wacław Sierpiński and Piers Bohl
, variants of this theorem continue to be studied to this day.
In 1916, Weyl proved that the sequence a, 22a, 32a, ... mod 1 is uniformly distributed on the unit interval. In 1935, Ivan Vinogradov proved that the sequence pn a mod 1 is uniformly distributed, where pn is the nth prime
. Vinogradov's proof was a byproduct of the odd Goldbach conjecture, that every sufficiently large odd number is the sum of three primes.
George Birkhoff, in 1931, and Aleksandr Khinchin, in 1933, proved that the generalization x + na, for almost all
x, is equidistributed on any Lebesgue measurable subset of the unit interval. The corresponding generalizations for the Weyl and Vinogradov results were proven by Jean Bourgain
in 1988.
Specifically, Khinchin showed that the identity
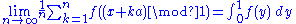
holds for almost all x and any Lebesgue integrable function ƒ. In modern formulations, it is asked under what conditions the identity

might hold, given some general sequence
bk.
One noteworthy result is that the sequence 2ka mod 1 is uniformly distributed for almost all, but not all, irrational a. Similarly, for the sequence bk = 2 k, for every irrational a, and almost all x, there exists a function ƒ for which the sum diverges. In this sense, this sequence is considered to be a universally bad averaging sequence, as opposed to bk = k, which is termed a universally good averaging sequence, because it does not have the latter shortcoming.
A powerful general result is Weyl's criterion
, which shows that equidistribution is equivalent to having a non-trivial estimate for the exponential sum
s formed with the sequence as exponents. For the case of multiples of a, Weyl's criterion reduces the problem to summing finite geometric series.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the equidistribution theorem is the statement that the sequence
- a, 2a, 3a, ... mod 1
is uniformly distributed on the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
, when a is an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. It is a special case of the ergodic theorem.
History
While this theorem was proved in 1909 and 1910 separately by Hermann WeylHermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
, Wacław Sierpiński and Piers Bohl
Piers Bohl
Piers Bohl was a Latvian mathematician, who worked in differential equations, topology and quasi-periodic functions....
, variants of this theorem continue to be studied to this day.
In 1916, Weyl proved that the sequence a, 22a, 32a, ... mod 1 is uniformly distributed on the unit interval. In 1935, Ivan Vinogradov proved that the sequence pn a mod 1 is uniformly distributed, where pn is the nth prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. Vinogradov's proof was a byproduct of the odd Goldbach conjecture, that every sufficiently large odd number is the sum of three primes.
George Birkhoff, in 1931, and Aleksandr Khinchin, in 1933, proved that the generalization x + na, for almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
x, is equidistributed on any Lebesgue measurable subset of the unit interval. The corresponding generalizations for the Weyl and Vinogradov results were proven by Jean Bourgain
Jean Bourgain
Jean Bourgain is a Belgian mathematician. He has been a faculty member at the University of Illinois, Urbana-Champaign and, from 1985 until 1995, professor at Institut des Hautes Études Scientifiques at Bures-sur-Yvette in France, and since 1994 at the Institute for Advanced Study in Princeton,...
in 1988.
Specifically, Khinchin showed that the identity
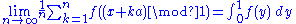
holds for almost all x and any Lebesgue integrable function ƒ. In modern formulations, it is asked under what conditions the identity

might hold, given some general sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
bk.
One noteworthy result is that the sequence 2ka mod 1 is uniformly distributed for almost all, but not all, irrational a. Similarly, for the sequence bk = 2 k, for every irrational a, and almost all x, there exists a function ƒ for which the sum diverges. In this sense, this sequence is considered to be a universally bad averaging sequence, as opposed to bk = k, which is termed a universally good averaging sequence, because it does not have the latter shortcoming.
A powerful general result is Weyl's criterion
Weyl's criterion
In mathematics, in the theory of diophantine approximation, Weyl's criterion states that a sequence of real numbers is equidistributed mod 1 if and only if for all non-zero integers \ell we have:...
, which shows that equidistribution is equivalent to having a non-trivial estimate for the exponential sum
Exponential sum
In mathematics, an exponential sum may be a finite Fourier series , or other finite sum formed using the exponential function, usually expressed by means of the functione = \exp.\,...
s formed with the sequence as exponents. For the case of multiples of a, Weyl's criterion reduces the problem to summing finite geometric series.
Historical references
- P. Bohl, (1909) Über ein in der Theorie der säkutaren Störungen vorkommendes Problem, J. reine angew. Math. 135, pp, 189–283.
- H. Weyl, (1910) Über die Gibbs'sche Erscheinung und verwandte Konvergenzphänomene, Rendiconti del Circolo Matematico di Palermo, 330, pp. 377–407.
- W. Sierpinski, (1910) Sur la valeur asymptotique d'une certaine somme, Bull Intl. Acad. Polonmaise des Sci. et des Lettres (Cracovie) series A, pp. 9–11.
Modern references
- Joseph M. Rosenblatt and Máté Weirdl, Pointwise ergodic theorems via harmonic analysis, (1993) appearing in Ergodic Theory and its Connections with Harmonic Analysis, Proceedings of the 1993 Alexandria Conference, (1995) Karl E. Petersen and Ibrahim A. Salama, eds., Cambridge University Press, Cambridge, ISBN 0-521-45999-0. (An extensive survey of the ergodic properties of generalizations of the equidistribution theorem of shift maps on the unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
. Focuses on methods developed by Bourgain.) - Elias M. Stein and Rami Shakarchi, Fourier Analysis. An Introduction, (2003) Princeton University Press, pp 105–113 (Proof of the Weyl's theorem based on Fourier Analysis)

